注重考题分析 突破解题瓶颈
王仙锋 铁志荣


摘要:《不等式选讲》作为新课标高考选考内容之一,考题难度适中,近几年的考题更注重对数学思想和数学方法的考查,通过历届高考试题的研究,分析题型、剖析方法、把握考点,提高学生分析解决此类问题的能力.
关键词:不等式;绝对值;参数;证明
作为新课标高考选考内容之一的《不等式选讲》,是对以前所学不等式知识的加强、延伸和深化.通过不等式的证明、不等式的几何意义、不等式的背景,从不等式的数学本质上加以剖析,从而提高逻辑思维能力、分析问题和解决问题的能力主要包括不等式的知识(绝对值不等式的性质)、证明不等式的方法(比较法,综合法,分析法,反证法,放缩法和数学归纳法)、几个重要的不等式(基本不等式,二维形式,向量形式和一般形式的柯西不等式,排序不等式)等内容.重点考查绝对值不等式的解法、含绝对值号函数的作图及函数图象间的关系、解含參数的绝对值不等式问题以及利用重要不等式对—些简单不等式的证明等;考查利用分类讨论思想、数形结合思想、函数与方程思想解决问题的能力,考试难度适中,本文就《不等式选讲》在新课标高考中的考点和题目类型以例说明.
1含绝对值符号函数图象的作法和绝对值不等式的解法
例1(2016年全国I卷)已知函数f(x)=|x+1|-|2x-3|.
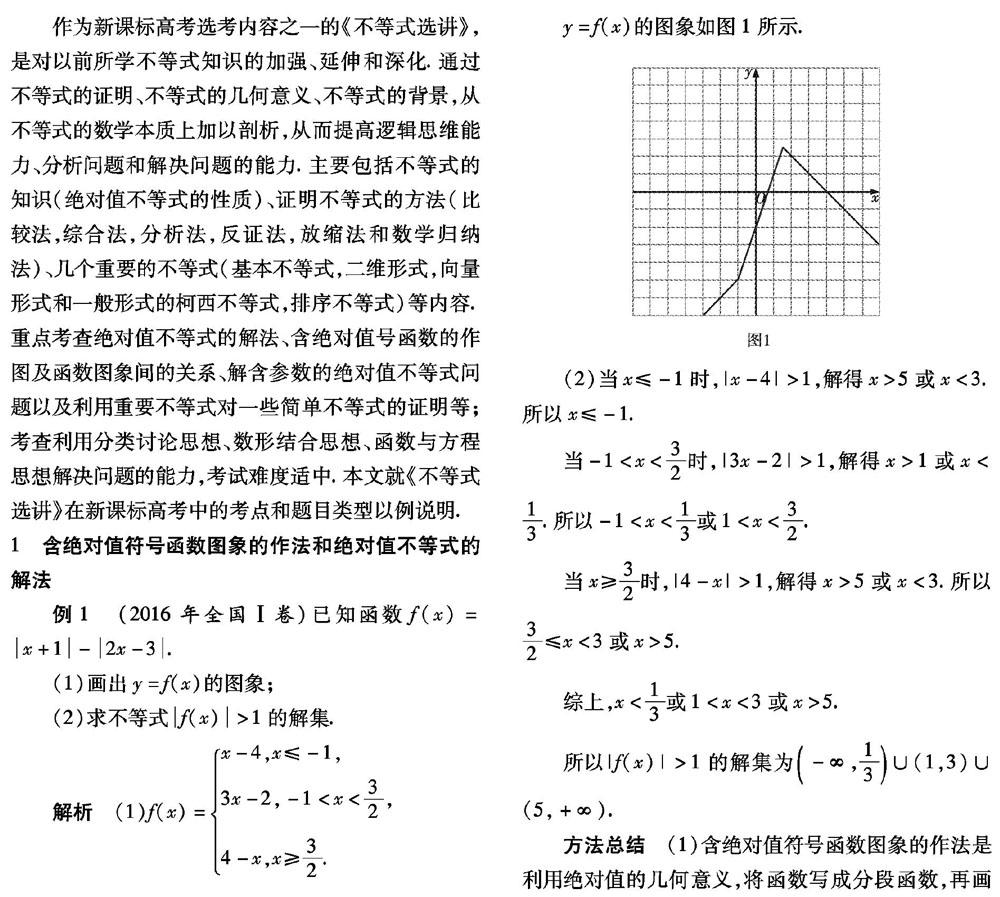
(1)画出y=f(x)的图象;
(2)求不等式|f(x)|>1的解集.
解析(1)f(x)={{{
(2)当x≤-1时,|x-41>1,解得x>5或x<3.所以x≤-1.
当-1
当x≥-3时,14-x|>1,解得x>5或x<3.所以232≤x<3或x>5.
综上,x<-或1
所以!f(x)|>1的解集为(-∞,1/3)u(1,3)U(5,+∞).
方法总结(1)含绝对值符号函数图象的作法是利用绝对值的几何意义,将函数写成分段函数,再画出在各自定义域的图象;(2)通常绝对值不等式的解法有三种:法1:利用绝对值不等式的几何意义求解,体现了数形结合的思想;法2:利用“零点分段法”求解,体现了分类讨论的思想;法3:通过构造函数,利用函数的图象求解,体现了函数与方程的思想.一般方法是脱去绝对值符号转化为不含绝对值的不等式求解.通常要求:掌握不等式|x|
例2(2018年全国I卷)设函数f(x)=|2x+11+|x-1I.
(1)画出y=f(x)的图象;
(2)当x∈[0,+∞)f(x)≤ax+b,求a+b的最小值.
解析(1)f(x)={x+2,-二≤x<1,-3x,x<一,2l3x,x≥1.
y=f(x)的圖象如图2所示.
(2)由(1)知,y=f(x)的图象与y轴交点的纵坐标为2,且各部分所在直线斜率的最大值为3,故当且仅当a≥3且b≥2时,f(x)≤ax+b在[0,+∞)成立,因此a+b的最小值为5.
方法总结恒成立问题的一一个巧解是数形结合,使得代数问题几何化,既通俗易懂,又简洁直观.第(2)小题结合(1)小题中函数的图象可得a,b范围,进而得到a+b的最小值.
2求参数的值或范围
例3(2017年全国I卷)已知函数f(x)=-x2+ax+4,g(x)=|x+1|+|x-1|.
(1)当a=1时,求不等式f(x)≥g(x)的解集;(2)若不等式f(x)≥g(x)的解集包含[-1,1],求a的取值范围.
解析(1)当a=1时,不等式f(x)≥g(x)等价于x-x+|x+1I+1x-1|-4≤0.①
当x<-1时,①式化为x2-3x-4≤0,无解;当-1≤x≤1时,①式化为xx“-x-2≤0,从而-1≤x≤1;
当x>1时,①式化为x2+x-4≤0,从而1
所以f(x)≥g(x)的解集为{xI-1
(2)当x∈[-1,1]时,g(x)=2..
所以f(x)≥g(x)的解集包含[-1,1],等价于当x∈[-1,1]时f(x)≥2.
又f(x)在[-1,1]的最小值必为f(-1)与f(1)之一,所以f(-1)≥2且f(1)≥2,得-1≤a≤1.
所以a的取值范围为[-1,1].
方法总结本题考查解含有绝对值的不等式、已知不等式的解集所包含的区域求参数问题等基础知识.(1)利用零点分段法,把含有绝对值不等式问题转化为不含绝对值符号的不等式问题;(2)不等式f(x)≥g(x)的解集包含[-1,1],等价于不等式f(x)≥g(x)在区间[-1,1]上恒成立,再利用函数思想转化为关于a的不等式组,解不等式组,即可求出a的取值范围,这是恒成立问题的常用解法.
例4(2018年全国I卷)已知函数f(x)=|x+1|-|ax-1I.
(1)当a=1时,求不等式f(x)>1的解集;
(2)若x∈(0,1)时不等式f(x)>x成立,求a的取值范围.
解析(1)当a=1时,f(x)=|x+1I-|x-1I.
即f(x)={2x,-1
故不等式f(x)>1的解集为{x|x>;1/2}.
(2)当x∈(0,1)时,Ix+11-|ax-1I>x成立等价于当x∈(0,1)时lax-1I<1成立.
若a<0,则当x∈(0,1)时lax-1l≥1;
若a>0,lax-11<1的解集为0
综k,a的取值范围为(0,2].
方法总结(1)含有参数时,要针对参数的取值情况进行讨论;(2)涉及绝对值不等式的恒成立问题,常用方法是由绝对值的意义去掉绝对值符号:①把不等式恒成立运用分离参数法转化为求函数的最值;②画出函数的图象,应用数形结合的思想解决问题;(3)对含参数的绝对值函数求最值时,常用的方法是图象法和绝对值不等式性质法(运用|a+bl≤la|+|b|(a,b∈R)或la-bl≤la-c|+lc-bI(a,b∈R),但要注意取等号的条件)
5不等式的证明
例5(2016年全国I卷)已知函数f(x)=x+一,M为不等式f(x)<2的解集.
(1)求M;
(2)证明:当a,b∈M时,|a+b|<|1+ab|.解析(1)f(x)<2的解集(-1,1).
(2)由(1)知,当a,b∈M时,-1
方法总结不等式证明的常用方法有比较法、综合法分析法、反证法、放缩法和数学归纳法.本题是含绝对值符号的不等式,比较法是典型的证明方法.
例6(2015年全国I卷)设a,b,c,d均为正数,且a+b=c+d,证明:
(1)若ab>cd,则Va+b>NC+vd;
(2)√a+/6>NC+va是|a-6|<|c-d|的充要条件.
解析(1)因为(Va+vb)2=a+b+2√ab,(vc+√d)2=c+d+2√cd.
由题设a+b=c+d,ab>cd得(a+√6)°≥(vc+vd)2.
因此a+vb>(c+vd.
(2)(i)若|a-b|<|c-d|,则(a-b)2<(c-d)2.即(a+b)2-4ab<(c+d)2-4cd.
因为a+b=c+d,所以ab>cd.
由(1)得√a+~b>Nc+√d.
(ii)若Va+vb>Nc+rd,则(√a+v6)2>(Nc+Nd)2.即a+b+2√/ab>c+d+2√cd.
因为a+h=c+d,所以ab>cd.于是(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2.
因此|a-b|<|c-d|.
综上,va+v6>NC+va是|a-b|<|e-d|的充要条件.
方法总结通常无理不等式或分式不等式的证明要用分析法,即从要证的结论出发,逐步寻求使它成立的充分条件,直至所需条件为已知条件或一个成立的事实(定义、公理定理、性质或已证明的命题)从而得出要证的命题成立.这是一种“执果索因”的思考和证明方法,它更符合人们的思维规律,思路自然,利于思考.
例7(2014年I卷)若a>0,b>0,且一;b=√ab.
(1)求a3+b3的最小值;
(2)是否存在a,b使得2a+3b=6?并说明理由.
2 解析由√ab=→+1b~√at≥得ab≥2,且当a=b=v2时等号成立.
故a+b°≥2√aB≥4、2,且当a=b=/2时等号成立.所以a3+b3的最小值为4、2.
(2)由(1)知,2a+3b≥2v6√ab≥4/3.
由于4、3>6,从而不存在a,b,使得2a+3b=6.
方法总结用基本不等式求出ab的最小值是本题解决的关键.
总之,新课程高考中不等式选讲考查的是绝对值不等式的各种解法和简单不等式的证明,解决的方法是紧扣绝对值的意义和不等式常用的证明方法。

