一类条件为abc=1的不等式

广东省中山市中山纪念中学 (邮编：528454 )

在不等式中,经常遇到条件为abc=1的不等式,比如越南不等式专家Can-Hang的一个经典结论,本文称之为定理1.

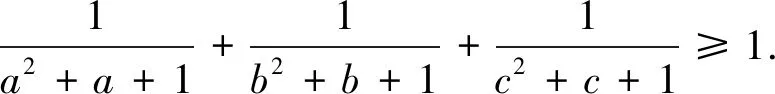
在证明定理1之前,首先给出本文要用到的不等式.

1 三元均值不等式及常见结论

(2)a、b、c∈R,a2+b2+c2≥ab+bc+ca;

(3)a、b、c∈R,(ab+bc+ca)2≥3abc(a+b+c).

2 三元柯西不等式及常见结论

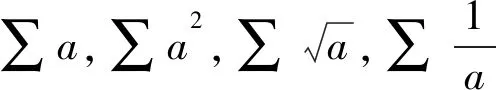
于是得到以下结论:

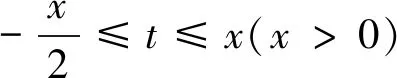
有了结论1,笔者利用柯西不等式并结合待定系数法来证明定理1.

由柯西不等式有

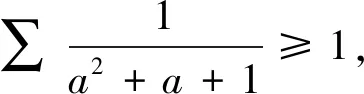
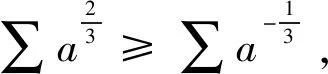
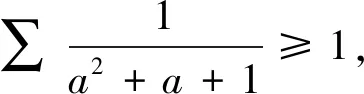
利用定理1,可快速地证明例1.

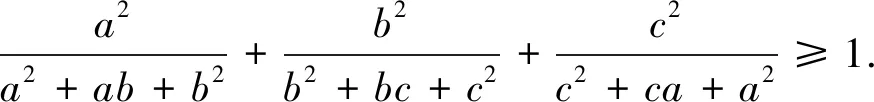
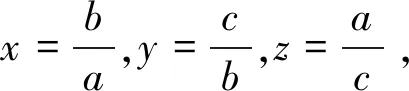
由xyz=1和定理1得证.

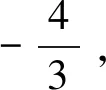
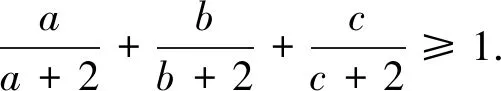
证明由柯西不等式有

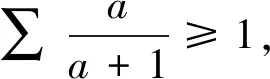
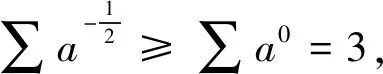
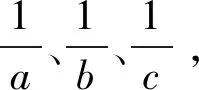
(2)经过简单变形,可得到以下式子:

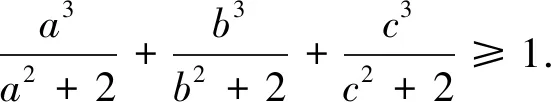
证明由柯西不等式有

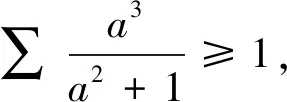
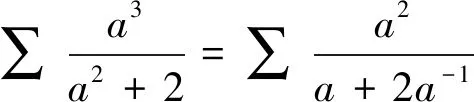
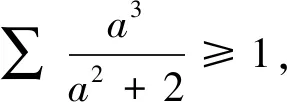
利用柯西不等式证明此类条件为abc=1的不等式的关键是创设应用柯西不等式的条件,配合一定的变形、构造技巧,这样可使复杂问题简单化,达到事半功倍的效果.若所证不等式的结构较简单,注意到柯西不等式的结论中分子部分的指数为偶数,此时无需利用待定系数法,经过简单尝试和配凑即可利用柯西不等式变形,并利用结论1或均值不等式解决问题.

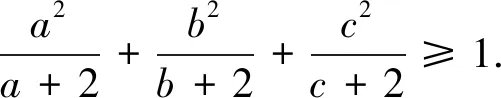
证明由柯西不等式有

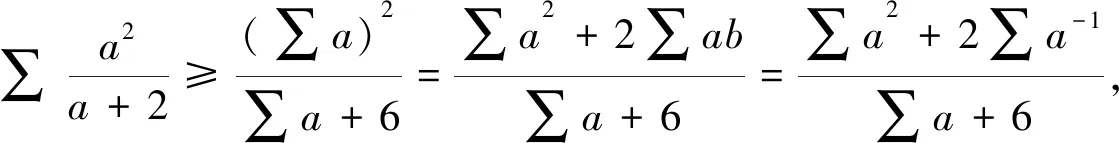
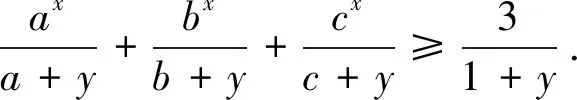
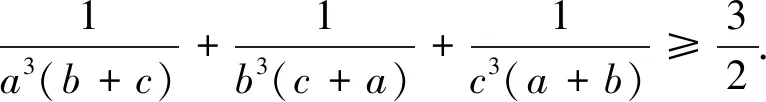
证明由柯西不等式有

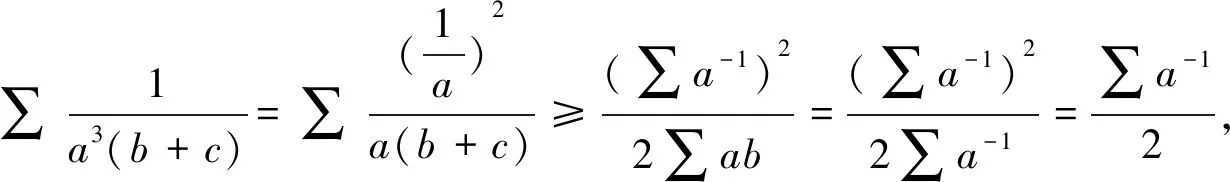
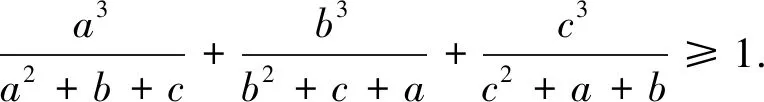
证明由柯西不等式有

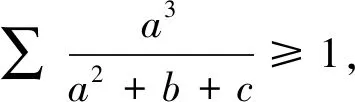
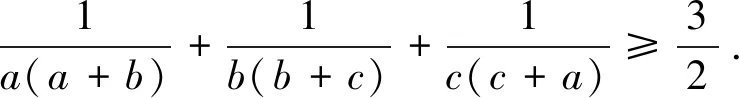
证明由柯西不等式有

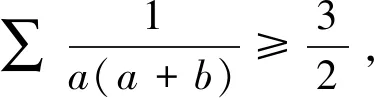
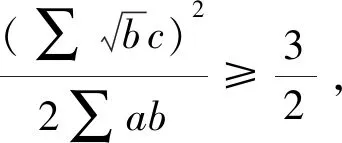
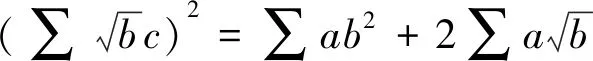
所以不等式得证.

不等式证明往往没有通法,也没有固定的模式,方法巧妙而灵活.均值不等式和柯西不等式是两个非常重要的不等式,也是证明其他不等式常用的方法和工具.下面再给出几个条件为abc=1的不等式问题,并利用均值不等式和柯西不等式来证明.

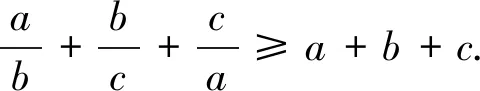
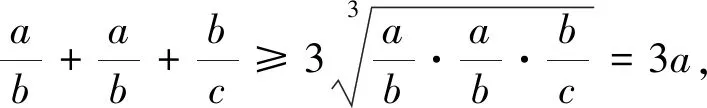
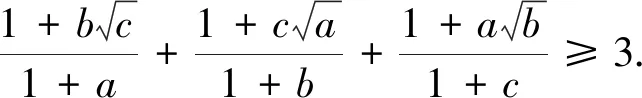
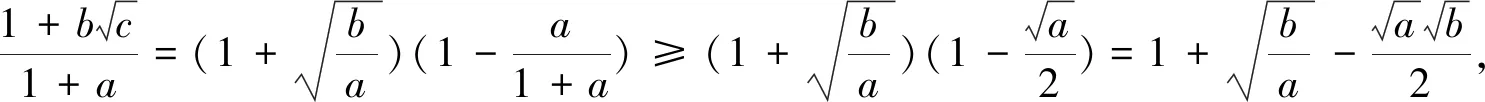
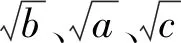
证明由柯西不等式，有

故不等式得证.

下面摘选一些条件为abc=1的不等式,留给有兴趣的读者.

设a、b、c>0,且abc=1,证明: