聚焦思维方法 指向问题本质
——对一道联赛题的探究与思考
浙江省温岭中学 (邮编:317500)
2017年9月10上午全国高中数学联赛一结束,笔者当日下午就参加了浙江赛区在杭州的阅卷工作.对第9题的批阅和同事的讨论,激发了对该题的深入探究.
1 试题展示

2 试题特点
本题作为解答题第1题(解答题共3题),它源于平时高考范围内的常见题,所涉及的知识不超过高考要求,但在有些处理手法上略有提高.本题语言简洁、解题入口宽、层次多,具有非常明显的区分度.数学素养一般的考生,通过对问题的合理分析,运用常规的讨论等方法,能够得到自己理想的结论,但是时间的成本会较大;而数学素养好、思维品质好的学生,能快速直达问题的本质,此题的本质在于分析抛物线的“陡峭程度”.因为k、m其实只影响f(x)=x2-kx-m的图象位置而不影响其形状,故本题其实是讨论f(x)=x2的图象中使得函数值差距不超过2的最长区间,即在分析抛物线的“陡峭程度”.
3 多视角下的方法探究
视角一三点法的视角
令f(x)=x2-kx-m,x∈[a,b], 则f(x)∈[-1,1], 于是
f(a)=a2-ka-m≤1
①
f(b)=b2-kb-m≤1
②
③
由 ①+②-③×2,得
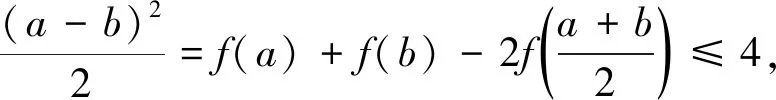

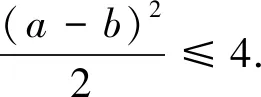
视角二对称轴讨论的视角
令M=f(x)max-f(x)min, 则M≤2 对任意x∈[a,b]恒成立.
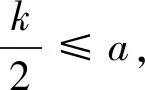
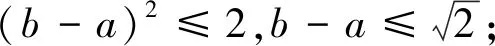
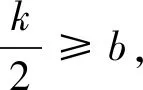
M=f(a)-f(b)=(a-b)(a+b-k)
≥(a-b)(a+b-2b)=(a-b)2,
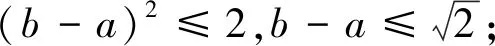
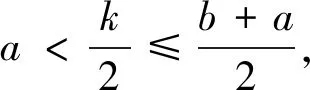
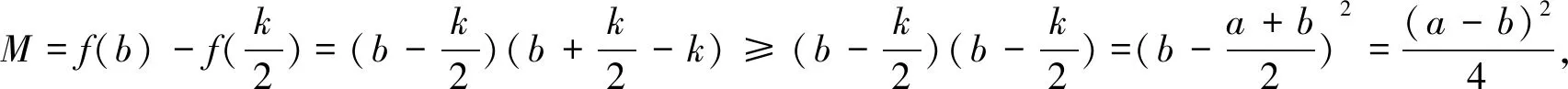
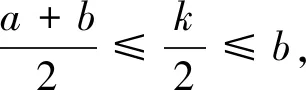
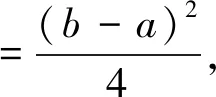

点评利用对称轴与区间的讨论,得出函数在区间上的单调性,然后得出M的表达式,再利用不等式放缩即可.大多数考生会从这个角度去思考和解题,他们能写出讨论的全部4种情况或者其中的几种情况. 一些优秀的学生会把(3)、(4)两种情况合起来:
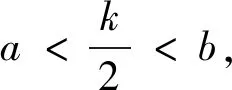

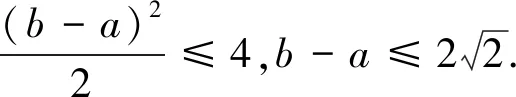
视角三最小值讨论的视角
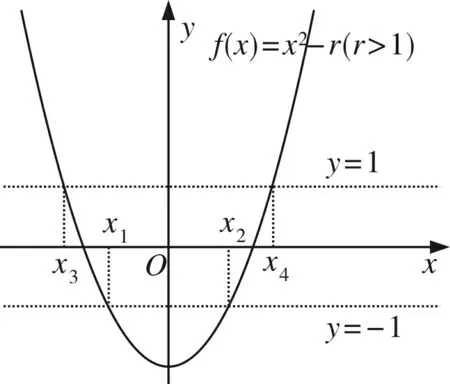
图1
不妨设f(x)=x2-r,x∈[a′,b′],b-a=b′-a′ ,下面对x∈R时,讨论f(x)的最小值,
(1)若f(x)min<-1, 即r>1,

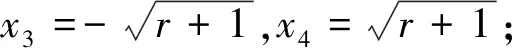

(2)若-1≤f(x)min≤1, 即-1≤r≤1,
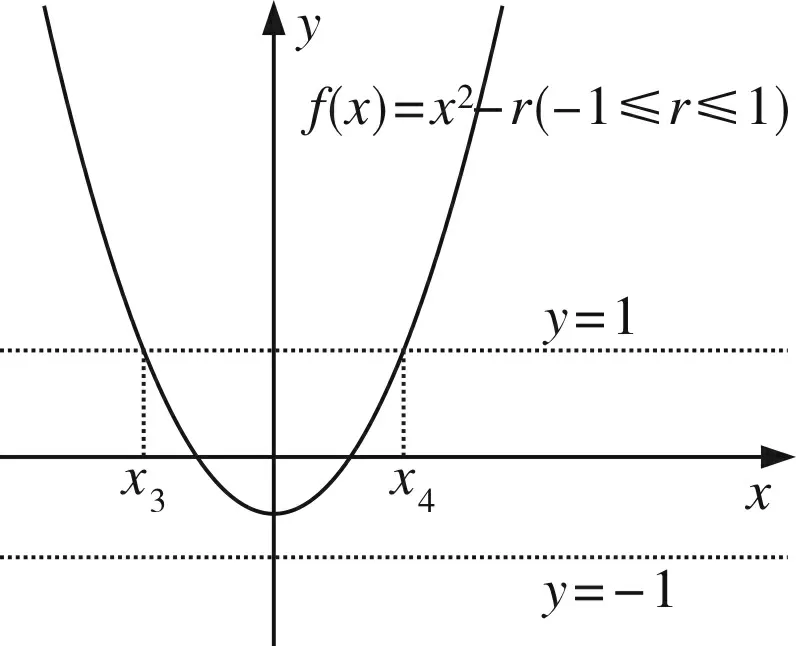
图2
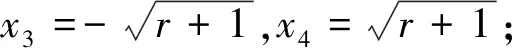
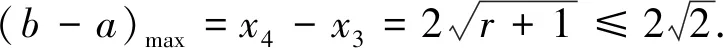
(3)若f(x)min>1, 则|f(x)|≤1 无解.

点评首先把f(x)视为f(x)=x2-r,这需要对二次函数有本质的理解,学生需要较好的数学素养,这样处理简化了后续的运算.其次此解法的本质是通过研究f(x)的图象与直线y=1 或y=-1交点的横坐标之差,来刻画b-a的范围.从具体的背景中抽象出一般的数量关系,概括出问题的本质,再从直观的图形角度来解决问题,认识了数与形的关系,在解决问题过程中,有利于培养学生直观想象的核心素养. 对上面的解法可进一步优化为:不妨设f(x)=x2-r,对∀x∈[a,b],均有|f(x)|≤1.
下面对r进行讨论.
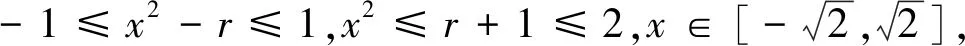

当r>1 时,由|f(x)|≤1,得-1≤x2-r≤1,r-1≤x2≤r+1,
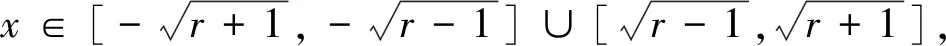
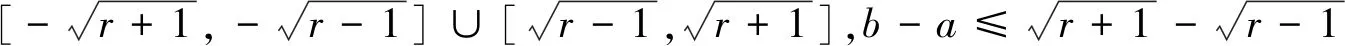

视角四反证法的视角
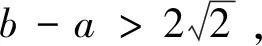
(1)若k≤2a或k≥2b, 则a+b-k≥b-a或a+b-k≤-(b-a),
|f(a)-f(b)|=|b-a||b+a-k|≥|b-a|2>8>2,
(2)若2a (3)若a+b 综上①、②、③知总存在x1、x2∈[a,b], 使|f(x1)-f(x2)|>2. 视角五函数凹凸性的视角 -1≤x2-kx-m≤1 对∀x∈[a,b] 恒成立,因为y=x2-kx-m为下凸函数, 即0≤(a-b)2≤8, 视角六竞赛的视角 由拉格朗日插值恒等式知 f(x)=x2-kx-m 比较上式两边x2的系数,得 整理得 (1)此题虽有着“入手易,解法多”的特点,但部分考生仍感觉力不从心.因此在平时的教学中应关注学生思维,重视问题的本质.张奠宙教授曾说:“数学教学的有效性关键在于对数学本质的把握、揭示和体验”.因此在平时教学中尽量留给学生足够的时间读题、审题,在这个过程中读出若干思维角度,审出题目结构,理解问题本质. (2)数学教学是“慢”艺术,若短时间内把所有好的数学思想方法打包发给学生,往往因空间不足而无法解压.因此,在教学中教师要敢于等待学生,陪伴学生重筑数学知识的形成之路,而不要在某些经典知识上一笔带过. (3)平时所谓的难题通常对多个知识点进行交叉和互融考察,数学素养较高的学生遇到难题时会把多种通法综合在一起,创造出含有“技巧性元素”的方法.因此,在平时的教学中,注重对知识“通性通法”的教学,通法就是遵循数学的思维特征分析问题和解决问题,只要对问题解决的通性通法熟练、高效,某些技巧性方法自然会应运而生. (4)注重高中数学与拓展知识之间的联系.比如函数的凹凸性、不动点理论、拉格朗日插值恒等式、极限思想等,其实平时试题中常会出现用琴生不等式秒杀的问题等.再如极限思想在函数零点判断问题中会常用到.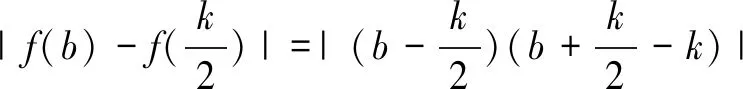
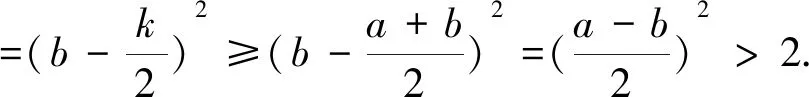
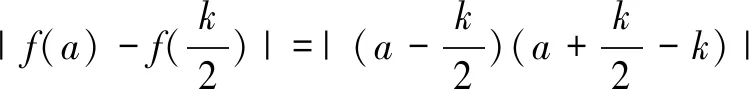

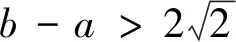
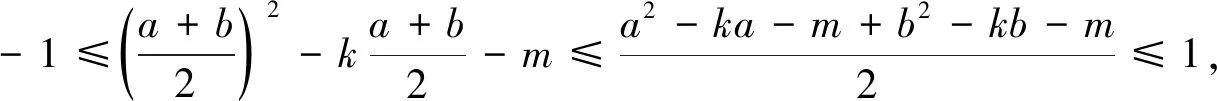



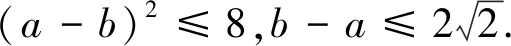
4 思考与建议

