格的模糊子集的模糊理想度
朱 翔,廖祖华
(1.江南大学 理学院 江苏 无锡 214122;2.无锡职业技术学院 基础课部 江苏 无锡 214121)
0 引言
逻辑代数,如Boole代数、MV代数、BL代数[1]等是人工智能基础理论研究的热点之一.在这些逻辑代数中,格是一种最基本的代数结构,它得到了人们的重视,并逐步发展成为一门独立的代数理论,被称为格论[2].格的理论在信息科学、计算机科学等领域有着重要的应用.1971年,Rosenfeld将模糊集理论应用到经典代数学中,提出了模糊群的概念.此后,国内外众多学者又将其他代数结构模糊化,模糊格代数便应运而生[3-5].文献[6]提出并研究了格上的模糊理想.此后,随着模糊理想的深入研究,格上的模糊理论得到了进一步的发展[7].
在模糊理论的应用中,引进了一系列“度”的概念对事物间的相似程度进行刻画[1].在模糊模式识别中,利用“贴近度”来度量两个模糊集的接近程度[8-9].学者将此思想应用到模糊逻辑代数的研究中,研究一个模糊子集成为某种模糊逻辑代数的程度.文献[10]提出了模糊子群度的概念,用以刻画一个模糊子集满足模糊子群条件的程度.文献[11]讨论了一个群的两个模糊子集乘积的子群度.文献[12]提出了环的模糊子环度的概念.利用该思想,王绪柱的研究团队近年来做了一系列的工作,得到了一些好的结果[13-16].
受上述思想的启发,本文提出了模糊理想度的新概念,用它来刻画格L的模糊子集成为模糊理想的程度.
1 预备知识
现介绍下文所需的格、格同态、理想、模糊理想、蕴涵、水平集、扩展原理、模糊直积等基本概念和性质.
定义1[2]设(L,≤)是偏序集,如果对于L中的任意一对元素a和b,sup{a,b}和inf{a,b}恒存在,则称(L,≤)是一个格.sup{a,b}和inf{a,b}分别记作a∨b和a∧b.
定义2[2]设f是格L→M上的一个映射,若∀x,y∈L,f满足条件:(1)f(x∨y)=f(x)∨f(y);(2)f(x∧y)=f(x)∧f(y),则称f是格L→M上的同态映射.若f是满射,则称f是满同态映射;若f是单射,则称f是单同态映射;若f是双射,则称f是同构映射.
定义3[2]设L是格,∅≠J⊆L.若(1) ∀x,y∈J,有x∨y∈J;(2) ∀x∈J,∀y∈L,有x∧y∈J,则称J是L的一个理想.
定义4[6]设A是格L的模糊子集,若对L中任意元素x,y,有:A(x)∧A(y)≤A(x∨y);A(x)≤A(x∧y),则称A是L的模糊理想.
定义5[8]设映射I:[0,1]×[0,1]→ [0,1],若∀x,y,z∈[0,1]满足条件:(1)x≤y⟹I(x,z)≥I(y,z);(2)y≤z⟹I(x,y)≤I(x,z);(3)I(1,0)=0,I(0,0)=I(1,1)=1,则称映射I为一个模糊蕴涵算子. ∀x,y∈ [0,1],I(x,y)=∨{t∈[0,1]|x∧t≤y},显然I为一个蕴涵,该蕴涵称为由min生成的R-蕴涵,通常记为x→y.
蕴涵算子及取大、取小运算具有如下性质.
命题1[17]设a,ai∈[0,1],i∈I(I为任意指标集),则:
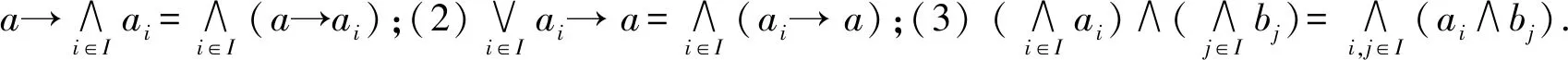
定义6[8]设A为格L的模糊子集,b∈[0,1],记A[b]={x|A(x)≥b,x∈L},称A[b]为A的水平集;记A(b)={x|A(x)>b,x∈L},称A(b)为A的强水平集.
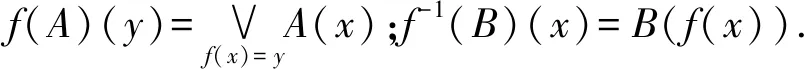
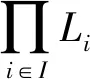
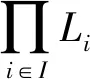
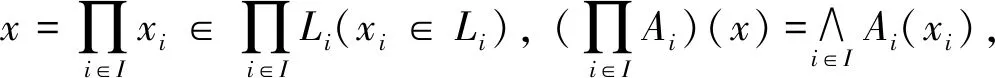

2 模糊理想度
现将给出模糊理想度的定义,讨论它的基本性质并给出其等价刻画.最后将研究模糊子集簇的交、模糊直积以及一个模糊子集在同态映射下的模糊理想度问题.
定义10设A为格L中的模糊子集,记
称mL(A)为A的模糊理想度.为了下文叙述方便,令
B1(x,y)={t∈[0,1]|A(x)∧A(y)∧t≤A(x∨y) },B2(x,y)={t∈[0,1]|A(x)∧t≤A(x∧y) },
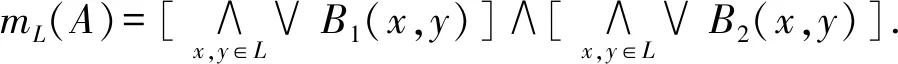
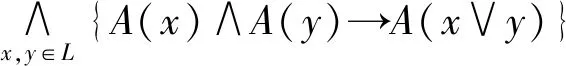
例1设Z是整数集,“≤”表示通常意义下的大小关系,则(Z,≤)构成一个格.定义A:Z→[0,1],
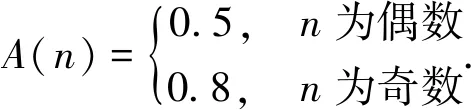
容易验证mL(A)=0.5.
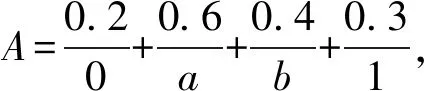
定理1设A是格L的一个模糊子集,则A为格L的模糊理想⟺mL(A)=1.

下面讨论mL(A)的性质,由此给出其等价刻画.
引理1设A是格L上的一个模糊子集,则mL(A)≥a⟺A(x)∧A(y)∧a≤A(x∨y)且A(x)∧a≤A(x∧y)(∀x,y∈L).

定理2设A是格L上的一个模糊子集,且mL(A)>0.令K1={a∈(0,1]|A(x)∧A(y)∧a≤A(x∨y),∀x,y∈L};K2={a∈(0,1]|A(x)∧a≤A(x∧y),∀x,y∈L};K3={a∈(0,1]|A(x)∧A(y)∧a≤A(x∨y),A(x)∧a≤A(x∧y),∀x,y∈L},则mL(A)=(∨K1)∧ (∨K2)=∨K3.
证明先证明mL(A)=∨K3.设mL(A)=c,由引理1得∀x,y∈L,A(x)∧A(y)∧c≤A(x∨y)且A(x)∧c≤A(x∧y).令b=∨K3,则易知b≥c.又∀ε>0,∃tε∈K3,使得tε>b-ε,且∀x,y∈L,A(x)∧A(y)∧tε≤A(x∨y)且A(x)∧tε≤A(x∧y).所以,A(x)∧A(y)∧(b-ε)≤A(x∨y)且A(x)∧(b-ε)≤A(x∧y).由ε的任意性可得,A(x)∧A(y)∧b≤A(x∨y)且A(x)∧b≤A(x∧y).再由引理1得mL(A)≥b,即c≥b,所以b=c.
下面证明(∨K1)∧(∨K2)=∨K3.∀a∈K3,则∀x,y∈L,有A(x)∧A(y)∧a≤A(x∨y)且A(x)∧a≤A(x∧y).因此a∈K1且a∈K2.故a≤∨K1且a≤∨K2.所以a≤(∨K1)∧(∨K2),从而∨K3≤(∨K1)∧(∨K2).令a1=∨K1,a2=∨K2,则∀ε>0,∃tε∈K1∩K2,使得tε>a1-ε,tε>a2-ε.令b=(∨K1)∧(∨K2),则a1≥b且a2≥b.所以tε>b-ε,tε>b-ε.又A(x)∧A(y)∧tε≤A(x∨y),A(x)∧tε≤A(x∧y),所以,A(x)∧A(y)∧(b-ε)≤A(x∨y),A(x)∧(b-ε)≤A(x∧y).由ε的任意性可得A(x)∧A(y)∧b≤A(x∨y),A(x)∧b≤A(x∧y).由引理1得,mL(A)≥b,即∨K3≥b.
综上所述,(∨K1)∧(∨K2)=∨K3.
我们知道,模糊理想与水平集具有密切的联系.接下来,我们将研究模糊理想度与水平集的关系,并利用水平集给出模糊理想度的等价刻画.
引理2设A是格L上的一个模糊子集,且mL(A)=c>0,则∀b∈(0,c],若A[b]≠∅,则A[b]是L的理想.
证明∀b∈(0,c],若A[b]≠∅,则∀x,y∈A[b],z∈L,有A(x)≥b,A(y)≥b.因为mL(A)=c,由引理1可得:A(x∨y)≥A(x)∧A(y)∧c≥b∧c=b;A(x∧z)≥A(x)∧c≥b∧c=b.所以,x∨y∈A[b]且x∧z∈A[b].从而A[b]是L的理想.对于强截集也有类似于上述的结论.
引理3设A是格L上的一个模糊子集,且mL(A)=c>0,则∀b∈[0,c),若A(b)≠∅,则A(b)是L的理想.
证明∀b∈[0,c),若A(b)≠∅,则∀x,y∈A(b),z∈L,有A(x)>b,A(y)>b.因为mL(A)=c,由引理1可得:A(x∨y)≥A(x)∧A(y)∧c>b;A(x∧z)≥A(x)∧c>b.所以,x∨y∈A(b)且x∧z∈A(b).从而A(b)是L的理想.
定理3设A是格L上的一个模糊子集,且mL(A)>0,则mL(A)=∨{a∈(0,1]|∀b∈(0,a],A[b]≠∅是L的理想}.
证明令mL(A)=c,B={a∈(0,1]|∀b∈(0,a],A[b]≠∅是L的理想},由引理2可得,c∈B,所以∨B≥c,即∨B≥mL(A).下面证明∨B≤mL(A)即可.先证明:∀a∈B,∀x,y∈L,有A(x)∧A(y)∧a≤A(x∨y).若不然,∃x0,y0∈L,使得A(x0)∧A(y0)∧a>A(x0∨y0).令A(x0)∧A(y0)∧a=b,则b∈(0,a],A(x0),A(y0)≥b,即x0,y0∈A[b]且A(x0∨y0) 综上所述,mL(A)=∨B=∨{a∈(0,1]|∀b∈(0,a],A[b]≠∅是L的理想}. 定理4设A是格L上的一个模糊子集,且mL(A)>0,则mL(A)=∨{a∈(0,1]|∀b∈[0,a],A(b)≠∅是L的理想}. 证明令mL(A)=c,B=∨{a∈(0,1]|∀b∈[0,a],A(b)≠∅是L的理想},由引理3可得,c∈B,所以∨B≥c,即∨B≥mL(A).下面证明∨B≤mL(A)即可.先证明:∀a∈B,∀x,y∈L,有A(x)∧A(y)∧a≤A(x∨y).若不然,∃x0,y0∈L,使得A(x0)∧A(y0)∧a>A(x0∨y0).令A(x0∨y0)=b,则A(x0),A(y0)>b即x0,y0∈A(b)且a>b.又因为当b 综上所述,mL(A)=∨B=∨{a∈(0,1]|∀b∈[0,a],A(b)≠∅是L的理想}.下面我们讨论模糊子集运算的模糊理想度.首先,我们给出模糊子集簇交的模糊理想度与各模糊子集的模糊理想度的关系. 接下来,再讨论模糊子集在模糊直积运算下的模糊理想度. 定理6可推广到指标集I为任意非有限集的情形,但下面定理7的证明与定理6的证明有所不同. 所以,由定义10可得 最后,我们给出格上的一个模糊子集在同态映射下的像集与原像集的模糊理想度的关系. 定理8设f:L1→L2为格同态,A、B分别为L1和L2上的模糊子集,且mL1(A),mL2(B)>0,则 (1)mL1(A)≤mL2(f(A));(2)mL2(B)≤mL1(f-1(B)). 证明(1) 由定理2及定义7可知, 推论1设A,B分别为格L1和L2上的模糊子集,且mL1(A),mL2(B)>0,那么(1) 若f:L1→L2为满同态映射,则mL2(B)=mL1(f-1(B));(2) 若f:L1→L2为单同态映射,则mL1(A)=mL2(f(A)). 为了衡量一个模糊子集构成模糊理想的程度,本文提出了模糊理想度的概念.通过对模糊理想度的研究,对模糊理想有了更深的认识,进一步丰富了格上的模糊理论.利用此思想,还可以度量格的其他类型的模糊理想,更进一步地还可以度量其他的模糊代数结构,同时也为模糊模式识别等应用领域提供一定的理论基础.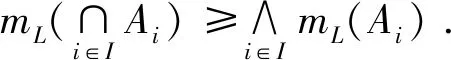
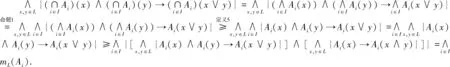
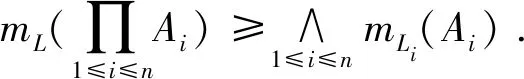
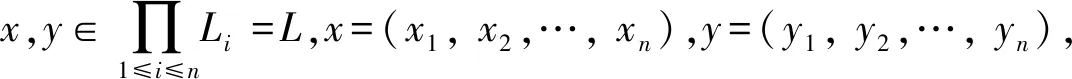

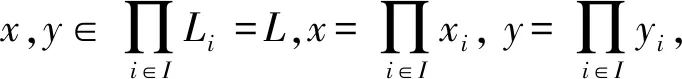
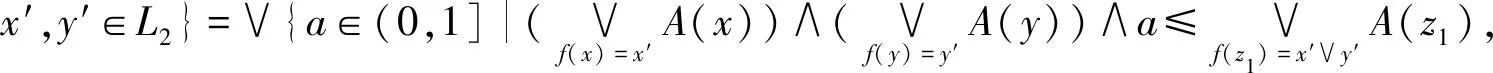
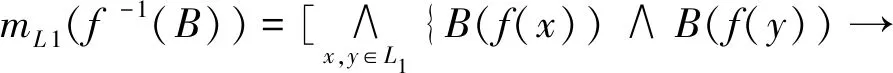

3 结语

