带扰动的随机微分方程的贝叶斯估计及其渐近性
2019-04-12 06:39:52谭慧玲
郑州大学学报(理学版) 2019年2期
谭慧玲,吕 艳
(南京理工大学 理学院 江苏 南京 210094)
0 引言
在概率空间(Ω,F,P)上,研究带扰动的随机微分方程
(1)
其中:θ∈Θ(Θ⊂R)为待估参数;0<ε≤1为扰动参数;Wt和Bt是相互独立的标准布朗运动;初始值(x0,y0)∈R×R.随机微分方程的参数状态往往是未知的,因此对随机系统中的参数估计也就成了实际应用中必须要解决的问题.目前,对于随机微分方程的参数研究,大部分都是对离散参数的估计[1],以及对参数的极大似然估计[2-3],而对于随机微分方程参数的贝叶斯估计的研究则不多.文献[4]证明了由分数布朗运动驱动的一类简单的线性随机微分方程的贝叶斯估计量的渐近正态性.文献[5]考虑了一类特定的一阶随机微分方程的贝叶斯估计问题,给出了当损失函数满足一定条件时,其参数的贝叶斯估计量的公式.相对于上述几种模型,本文考虑一类带扰动参数的随机微分方程的贝叶斯估计,并讨论了小扰动参数ε对估计量的影响.
1 θ的贝叶斯估计量

(2)
(3)
令θ0为参数θ在Θ中的一个真值,则由式(3)、Pθ相对于Pθ0的Radon-Nikodym导数为
(4)
由方程(1)可知
(5)
将方程(5)代入到式(4)中,整理可得
(6)

∀u∈Θ.
(7)
2 贝叶斯估计的渐近正态性
现在来讨论估计量的性质,P和E表示概率和期望.考虑随机过程ZT(u)=(dPθ0+u/λ(T))/(dPθ0),其中
(8)

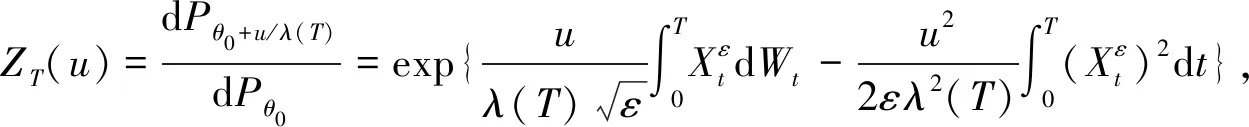
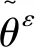
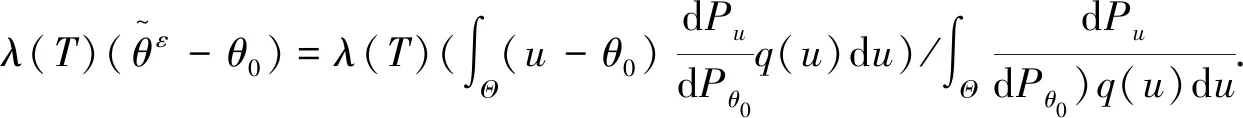
(9)
由引理1可知,当T→∞时,有
(10)
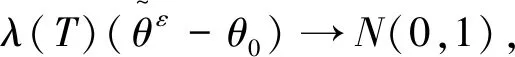
3 贝叶斯估计的渐近一致性

(11)
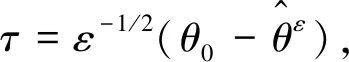
假设下列3个条件成立.


引理2假设条件a)~c)成立,则存在δ0>0,使得当ε→0时,有
证明由文献[13]可直接得到.
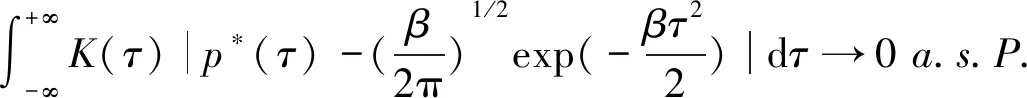
证明由引理2可得
(12)
令K(τ)≡1,则
(13)

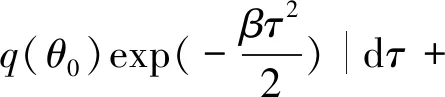
由式(12)、(13)和文献[5]可得,当ε→0时,上述不等式右侧趋于零,得证.

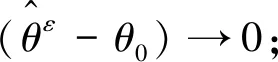

猜你喜欢
数学物理学报(2020年3期)2020-07-27 01:20:08
数学物理学报(2019年3期)2019-07-23 01:15:34
中学生数理化·中考版(2017年9期)2017-12-20 08:13:22
统计与决策(2017年2期)2017-03-20 15:25:23
现代营销·学苑版(2016年12期)2017-01-23 13:00:14
电测与仪表(2016年15期)2016-04-12 00:30:58
湖北师范大学学报(自然科学版)(2015年1期)2016-01-10 08:41:14
电测与仪表(2015年6期)2015-04-09 12:00:50
数学物理学报(2014年3期)2014-03-11 18:34:27
华东师范大学学报(自然科学版)(2014年4期)2014-03-11 16:18:25

