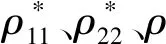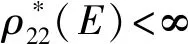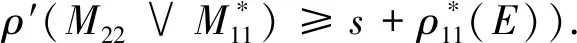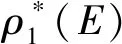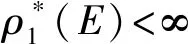两个独立空间拥有公共基的一些先决条件

毛 华

(河北大学 数学与信息科学学院 河北 保定 071002)

0 引言

拟阵[1]有着广泛的应用[2-6].根据Oxley[7]给出的无限拟阵内涵，独立空间(independence space)就是被研究的无限拟阵[8-14]，Welsh[14]提出一个有关独立空间的公开问题：“何时两个独立空间拥有一个公共基?”.到目前为止，该问题仅对一些特殊情况给予了解决[14-15].根据文献[14，16]中有限拟阵相关问题的回答、以及文献[7]带来的启发，本文将解答Welsh的部分问题.

1 预备知识

本文中，E代表某个任意的基数，也可能是无限的集合.对于一个集合S：P(S)是S的所有子集构成的集合；|S|是S的基数；sup{S}表示{S}的上确界；max{S}代表{S}中最大元；这里S中的偏序为集合的包含关系.对于任何的X，Y⊆E，Y⊂⊂X表示Y是X的一个有限子集.Z+代表非负整数集.

文献[7] 分别给出算子f、f*的定义，一个集合是f-独立的、f-相关的、f-支撑的、f的一个基的定义、还有幂等-交换或称IE-算子的定义.文献[7，14]给出一个准-独立空间Mp的定义、Mp中的独立集、基的定义.文献[14] 提供Mp的秩函数定义.文献[7，14]还给出一个独立空间M的定义、M中的独立集、基的定义.文献[7]有B-拟阵MB的定义.文献[7]有MB的闭包算子(closure operator)的定义.文献[14]中给出独立空间的闭包算子的定义.文献[14，16]提供拟阵MM的定义、MM的独立集、基、秩函数的定义.

引理1令(Ij：j∈J)为E上的准-独立空间族，其秩函数为ρj(j∈J).令∨j∈JIj={X：X=∪j∈JAj，Aj∈Ij}，并且称这一集合族为准-独立空间(Ij：j∈J)的并，记为∨j∈JMj.可以证明准-独立空间(Ij：j∈J)的并是一个准-独立空间[14].若B1和B2都是一个独立空间的基，那么|B1|=|B2|.设M=(E，I)是一个独立空间，并且ρ是它的秩函数，还有X⊆E.那么(X，I|X)是X上的一个独立空间，用M|X表示，此处I|X={Y⊆X：Y∈I}.易证明对于Y⊆X，有r(Y)=ρ(Y)，此处r是M|X的秩函数.进而X的秩r(X)将是独立空间M|X的秩[7].

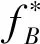
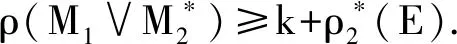
(1) 易知对于∀X，Y⊆E，若X⊆Y，则ρp(X)≤ρp(Y)，此处ρp是一个准-独立空间(E，Ip)的秩函数.独立空间M的秩函数ρ也如同Mp中的定义一样.从文献[7]可知，每个B-拟阵MB=(E，IB)是一个准-独立空间.因此，IB中的元也称为独立集，IB中的极大元也称为基，因而，MB的秩函数ρB与Mp中的定义一样.若M为E上的一个独立空间并且其秩函数是ρ，则有对于任意的X⊆E，ρ(X)=ρB(X)=ρp(X)，此处ρB、ρp分别是B-拟阵M的秩函数与准-独立空间M的秩函数.若一个独立空间M被作为一个B-拟阵MB，那么M的基集合BM与MB的基集合BMB是一样的(MB=M).也就是说，B∈BM⟺B∈BMB成立.

(2) 令X⊆E.若f是E上的一个IE-算子，此处|E|<∞，则f是E上的一个有限拟阵的闭包算子.对于E上的一个算子f，f*是E上的一个算子并且(f*)*=f.从而，若f是一个IE-算子，则f*亦然.关于f-的独立集集合恰恰是关于f*-的支撑集的补集.关于f-的基恰好是f*-的基的补集.

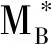
(4) 对于一个准-独立空间Mp=(E，Ip)，不难证明对于任意的X⊆E，有(X，Ip|X)是一个准-独立空间，记为Mp|X，此处Ip|X={Y⊆X：Y∈Ip}.另外，rp(Y)=ρp(Y)成立，此处rp、ρp分别是Mp|X、Mp的秩函数，并且Y⊆X.

由引理1以及上面的讨论，可得(M1∨…∨Mm)|X=(M1|X)∨… ∨(Mm|X)，此处X⊆E，而Mj是E上的一个准-独立空间(j=1，…，m<∞).本文中，ρp(Mp)有时也代表E的秩ρp(E).

2 回答

引理3设M=(E，I)为一个独立空间，且ρ为其秩函数.设ρ*是M*=(E，I*)的秩函数，此外，当考虑M为一个B-拟阵时，M*是M的对偶.那么ρ*(E)=|EB|，这里B是M的一个基.

证明从第1节中可以知道，M*是一个B-拟阵，也是一个准-独立空间.另外，对于X⊆E，必有

ρ*(X)=sup{|Y|：Y∈I*，Y⊂⊂X}.

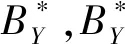
利用定义知两个独立空间M1=(E1，I1)、M2=(E2，I2)拥有一个独立集∅.下面讨论M1和M2拥有一个大小为k的独立集的情况，其中k≠0.

若X是M1和M2的一个公共独立集，则任何Y⊂⊂X也是M1和M2的公共独立集.因此，若寻找在何种条件下M1和M2拥有一个公共独立集X，则仅需考虑|X|<∞的情况.另外有以下结论.

(a) 若E1∩E2=∅，M1和M2有且仅有∅作为公共独立集.

(b) 若E1∩E2≠∅， 需要考虑M1|(E1∩E2)和M2|(E1∩E2)拥有公共的非空独立集.也就是说，需要考虑两个定义在同一个底集上的独立空间拥有公共基的情况.

基于上面的分析以及结论(a)、(b)，以下假设E1=E2.

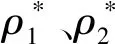
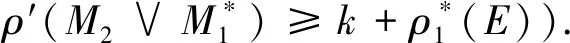
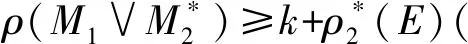
证明如果|E|<∞，所需结果在引理2中给出.下面考虑|E|≮∞.

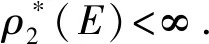
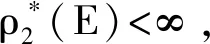
实验组和对照组操作技能考核成绩差异无显著性;实验组在自主学习的自我管理、学习合作维度上显著优于对照组，差异有显著性；实验组对案例教学法课堂教学质量的评价较高。

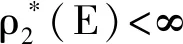
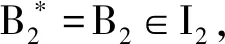
令Mj=(E，Ij)为一个独立空间，fj为其闭包算子(j=1，2)，设X为M1和M2的一个公共独立集.Y=f1(X)∩f2(X).由第1节，可以陈述为X是M1|Y和M2|Y的一个公共独立集；另外，ρM1|Y(Y)=ρM2|Y(Y)是成立的.反之，设Z⊆E.可以说，若X是M1|Z和M2|Z的一个公共基，则X是M1和M2的一个公共独立集；还有，ρM1|Y(X)=ρM2|Y(X)=|X|为正确的.即仅需解决若ρ1(E)=ρ2(E)，则M1和M2拥有一个公共基.

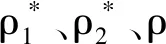
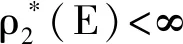
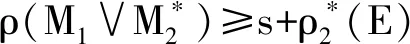
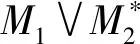
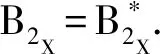
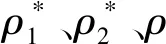
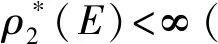
证明由引理2，对于|E|<∞的情况证明略.下面设|E|≮∞.

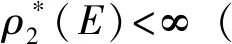
设Mj=(Ej，Ij)为一个独立空间且ρj为其秩函数(j=1，2).将分成几种情形来回答 Welsh的问题.

情形1E1∩E2=∅.

对M1和M2,无论何种事情发生，利用定义可知：∅将是M1和M2的一个公共独立集.但是，若I1≠{∅}或I2≠{∅}，则∅不是一个公共基.即在如此的假设下，M1和M2不存在公共基；若I1=I2={∅}，则∅是M1和M2的一个公共基.

情形2E1∩E2≠∅.

由引理1，对于Mj的任意一个基Bj，ρj(Ej)=|Bj| 成立，j=1，2.可用两种情形证明.

子情形2.1ρ1(E1)<ρ2(E2) (或者说ρ1(E1)>ρ2(E2)).可以得到|B1|<|B2|(或|B2|<|B1|).因此，M1和M2根本没有公共基.

子情形2.2ρ1(E1)=ρ2(E2)=γ.若γ=0，则∅是M1和M2的公共基.下面将处理γ≠0的情况.