收益可变泛化定向问题建模及优化算法研究
林丕源,张鑫睿,朱泽鹏,吴志辉,黄沛杰
(华南农业大学 数学与信息学院 广东 广州 510642)
0 引言
泛化定向问题(generalized orienteering problem,GOP) 是一类特殊的路径规划问题,最早由Wang等[1]于1996年提出.在该问题中,每个点有多个不同类型的收益,每个类型占有一定的权重比例,其目标是在一定的时间限制下访问多个点,使求得路径的收益最大.例如,在灾后搜救贵重物资时,每个救援点有多种不同类型、不同重要程度的待救物资.GOP是定向问题(orienteering problem,OP)[2]的扩展,都是NP-hard问题,现有的研究大多都集中使用启发式算法求解[1,3-5].
在搜救、物流运输[5]等泛化定向问题的实际应用场景中,往往还伴随着收益可变的情况.如在灾后搜救中的各种待救物资,其价值会随着救援时间的延长而面临被毁的风险;在低温冷链物流运输中,运输的各种物资其新鲜度也会随着运输时间的积累而降低,需要在有限的时间内寻找最优运输路线,以降低损失,获取最大收益.因此有必要研究多类型收益随时间下降变化的优化问题,称为收益可变泛化定向问题 (generalized orienteering problem with variable profits,GOPVP).本文对GOPVP进行建模,并提出了求解该问题的改进遗传算法(genetic algorithm,GA).
遗传算法受进化生物学的启发而发展,能保证种群的多样性,具有良好的全局寻优能力[6-7],被广泛应用于各类组合优化问题中.GA的改进主要在于遗传算子(选择、交叉、变异)的设计[8].在采用GA求解OP相关问题方面,Wang等[4]在求解GOP中采用了经典的选择和交叉算子,变异算子则采用了逆转变异.Zabielski等[9]则在求解OP中采用了锦标赛的选择算子,并综合采用了插入、删除和逆转的变异算子.由于GOPVP中收益随时间可变,解序列细微的变化将使目标函数值产生较大差异,导致难以搜索最优解.本文基于小生境[10]的选择思想,在选择算子方面,采用分组竞争的遗传策略,选择适应值较高的个体来保证子代的优越性,增加后续遗传算子搜寻全局最优解的概率.并应用和设计新的变异算子加强邻域精确搜索能力,进一步提高解的质量.实验结果表明,相比于研究进展方法,改进的遗传算法更具有效性和稳定性.
1 问题描述与建模
收益可变泛化定向问题描述如下:在一个无向完全图中,每个点有多个类型的收益,并随时间下降变化,各类型占有一定的权重.目标是在限定的时间内,求得一条从起点到终点的路径,且至多经过其他点一次,使得所获收益最大.本文采用文献[4]中使用的目标函数,结合可变收益的特点,给出GOPVP的数学模型.
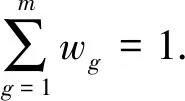
引入如下标记.
1)xij: 当边(i,j)∈E被访问时,记xij=1,否则为0.
2)ui: 表示点vi在路径中的位置.
GOPVP的数学模型为
(1)
(2)
(3)
(4)
2≤ui≤n,i≠1,
(5)
ui-uj+1≤(n-1)(1-xij),i,j≠1.
(6)
xij∈{0,1},i,j∈V,
(7)
其中:目标函数(1)表示最大化路径总收益;约束(2)保证路径的长度不超过最大时间约束Tmax;约束(3)保证从起点v1出发并到达终点vn;约束(4)确保结点至多被访问一次;约束(5)和(6)确保路径中没有子环,称之为Miller-Tucker-Zemlin (MTZ)[11].
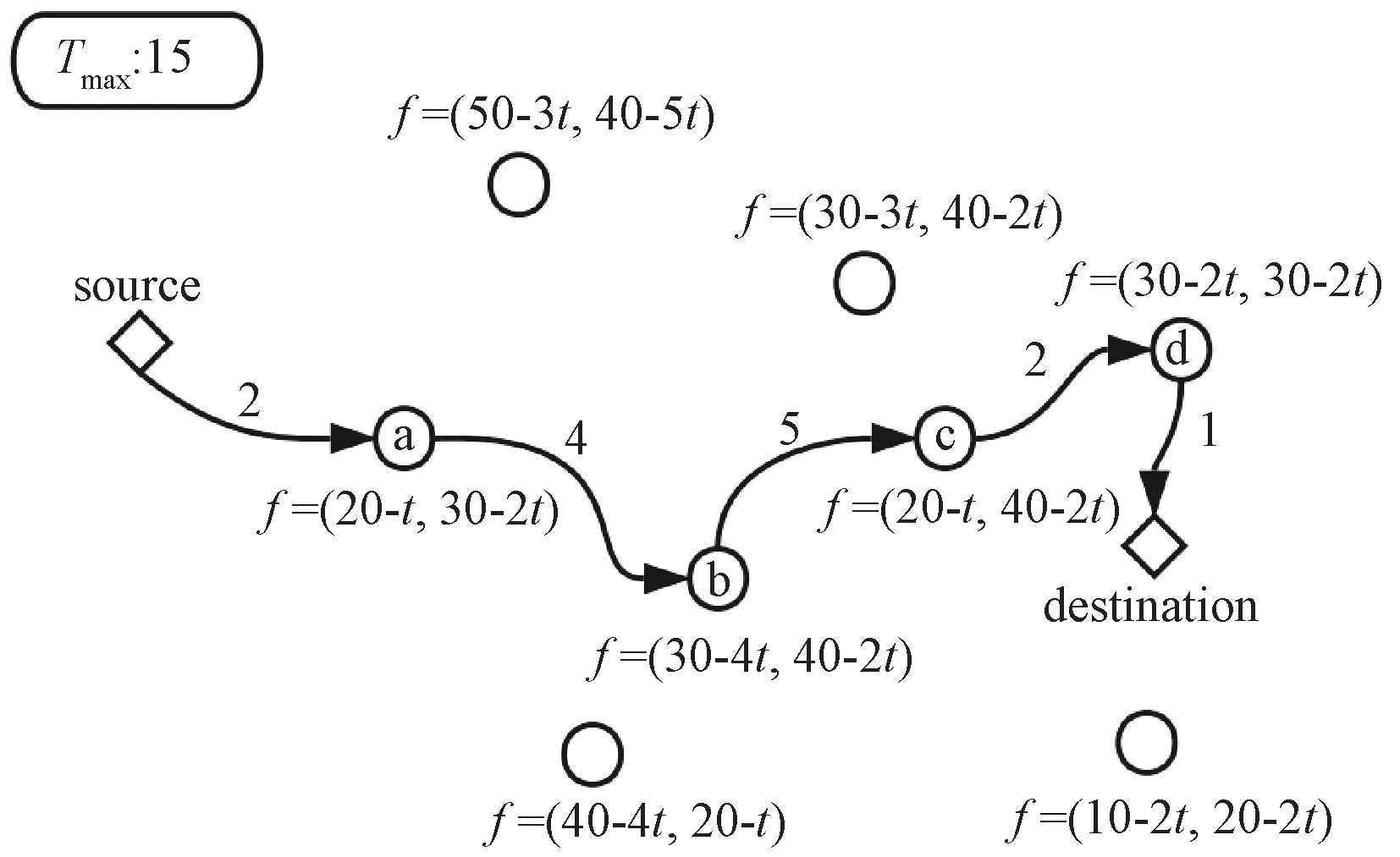
图1 GOPVP的一个示例解Fig.1 An example of solution of the GOPVP
图1展示了GOPVP的一个可行解示例.图中菱形表示起止点,圆形表示待访问点.最大时间约束Tmax为15,每个点有两个类型的收益,f表示结点的收益变化函数,边权表示两点之间的耗时(图中仅展示了部分结点间的时间花费).假设目标函数中指数k为1,两个类型权重均为0.5,点的收益随时间线性下降,具体如图所示.图1所示的路径中,为了保证在指定时限内到达目的点,有4个点未访问,路径为source-a-b-c-d-destination,路径总耗时为14,满足最大时间约束.根据目标函数公式(1),路径总收益为56.5.
2 算法求解
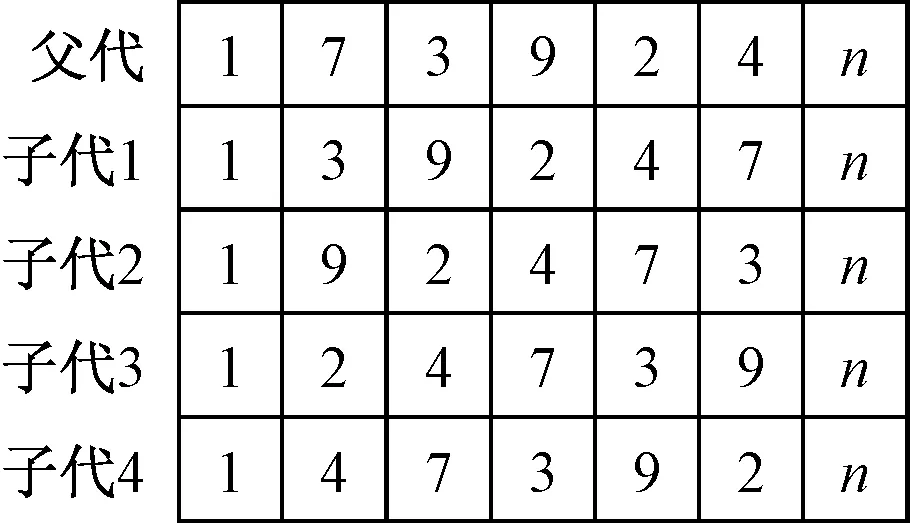
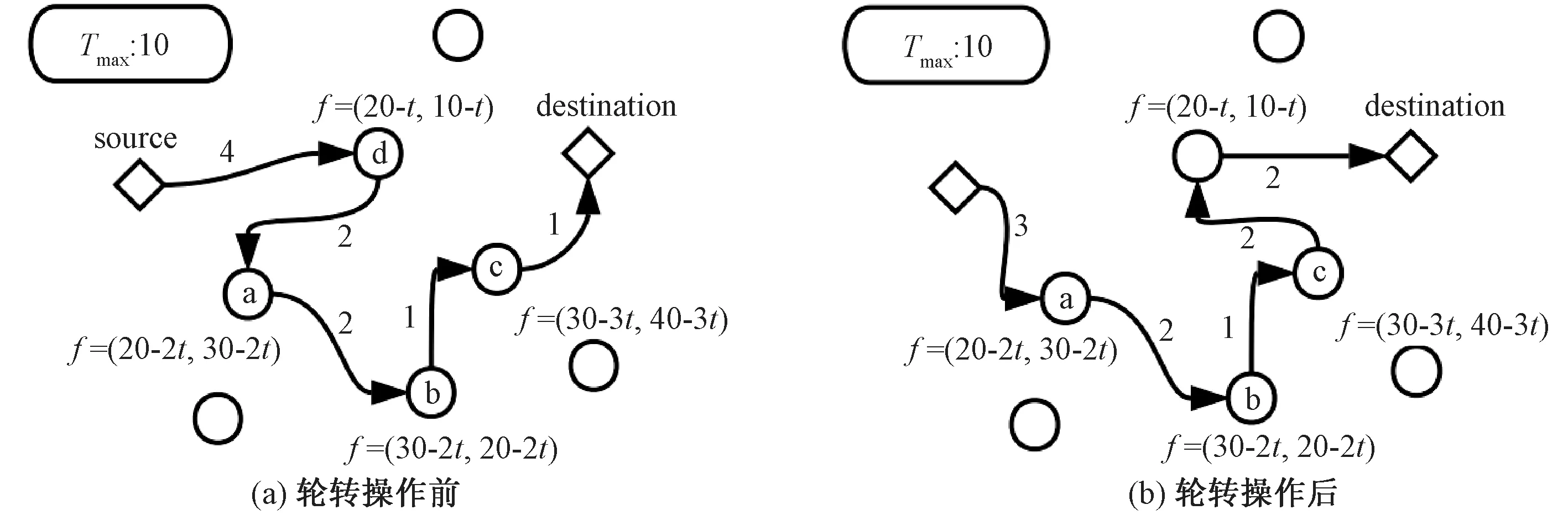
本文提出改进的遗传算法来求解GOPVP.首先随机初始化种群,随后通过分组竞争从父代中选择较优的个体形成较优的子代,交叉算子选取适当的父代进行交叉.变异算子除了基于GA求解OP相关问题的研究进展方法[4,9]中采用的插入、删除和逆转等变异算子之外,基于优化局部搜索策略[12-13]的考虑,增加了替换和交换两个变异算子,并针对收益变化的特点新增一个轮转变异算子,来进一步改善解的质量,以此形成更优种群.当进化次数达到设定的阈值或最优解多次没有提升时终止计算,否则重启算法.
2.1 染色体编码及适应值计算
本文采用自然数编码的方式,将完全图中的各点标序.当染色体为1-8-2-9-3-7-6-n时,表示求解路径从序号为1的点出发,依次经过中间各结点,到达终点n.本文使用目标函数值来表示个体的适应值,
(8)
2.2 初始化种群
本算法采用随机生成方式初始化种群.首先固定起止点,形成仅有两个基因的染色体,接着向染色体中插入新的基因,同时判断插入后的新染色体是否违反条件约束,若违反,则终止插入新的基因,否则选择下一个基因顺序插入.
2.3 遗传算子
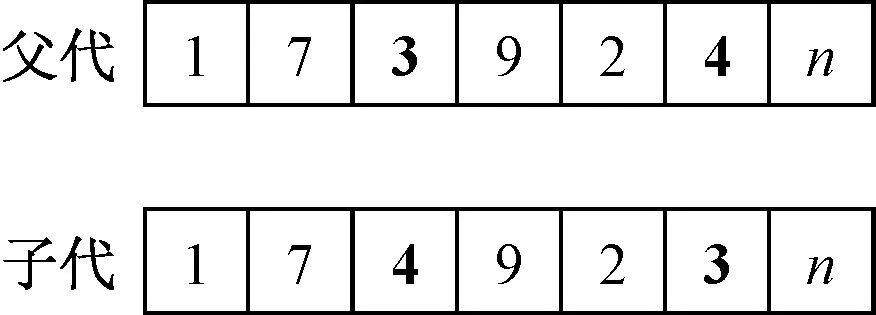
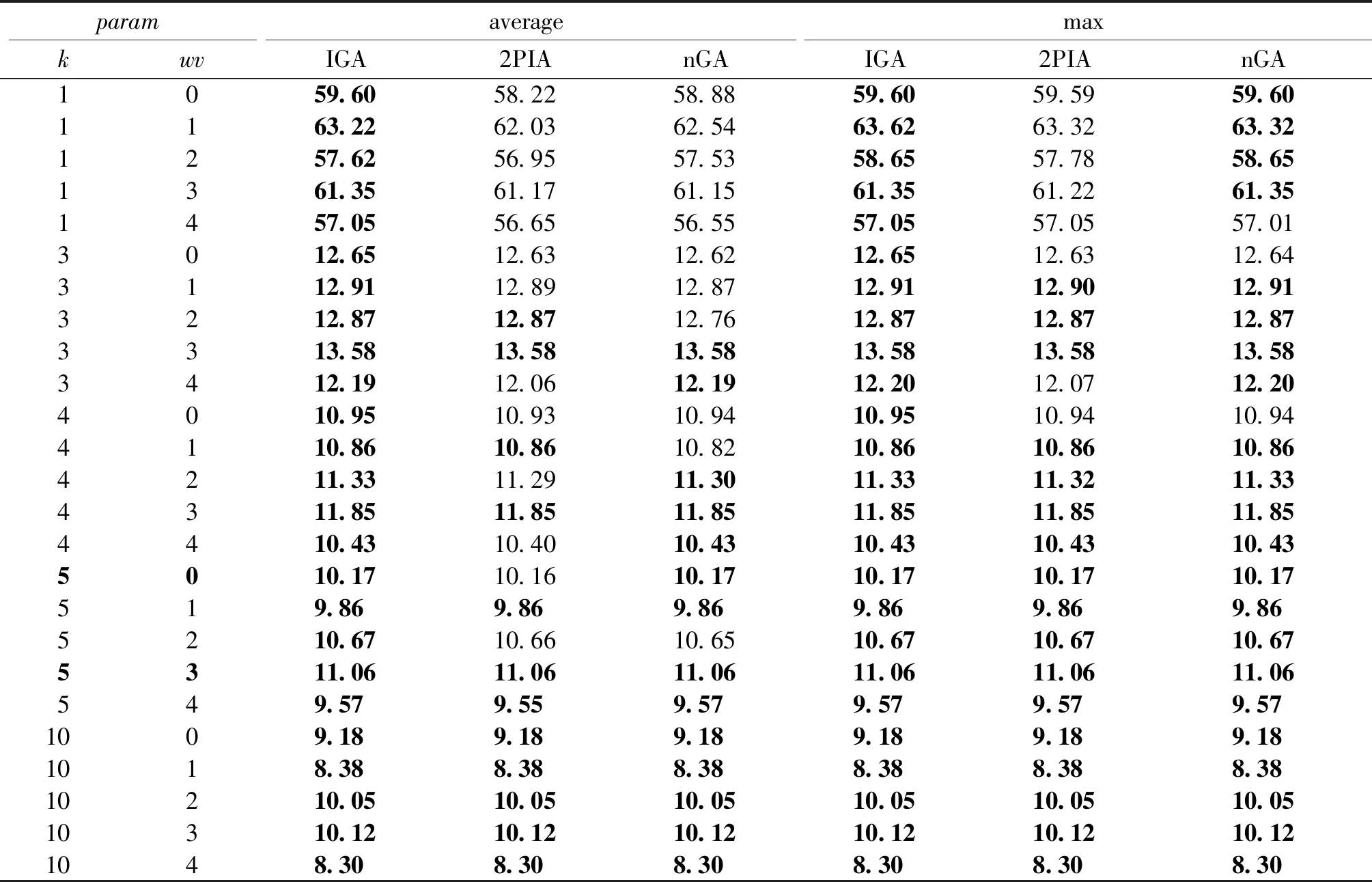
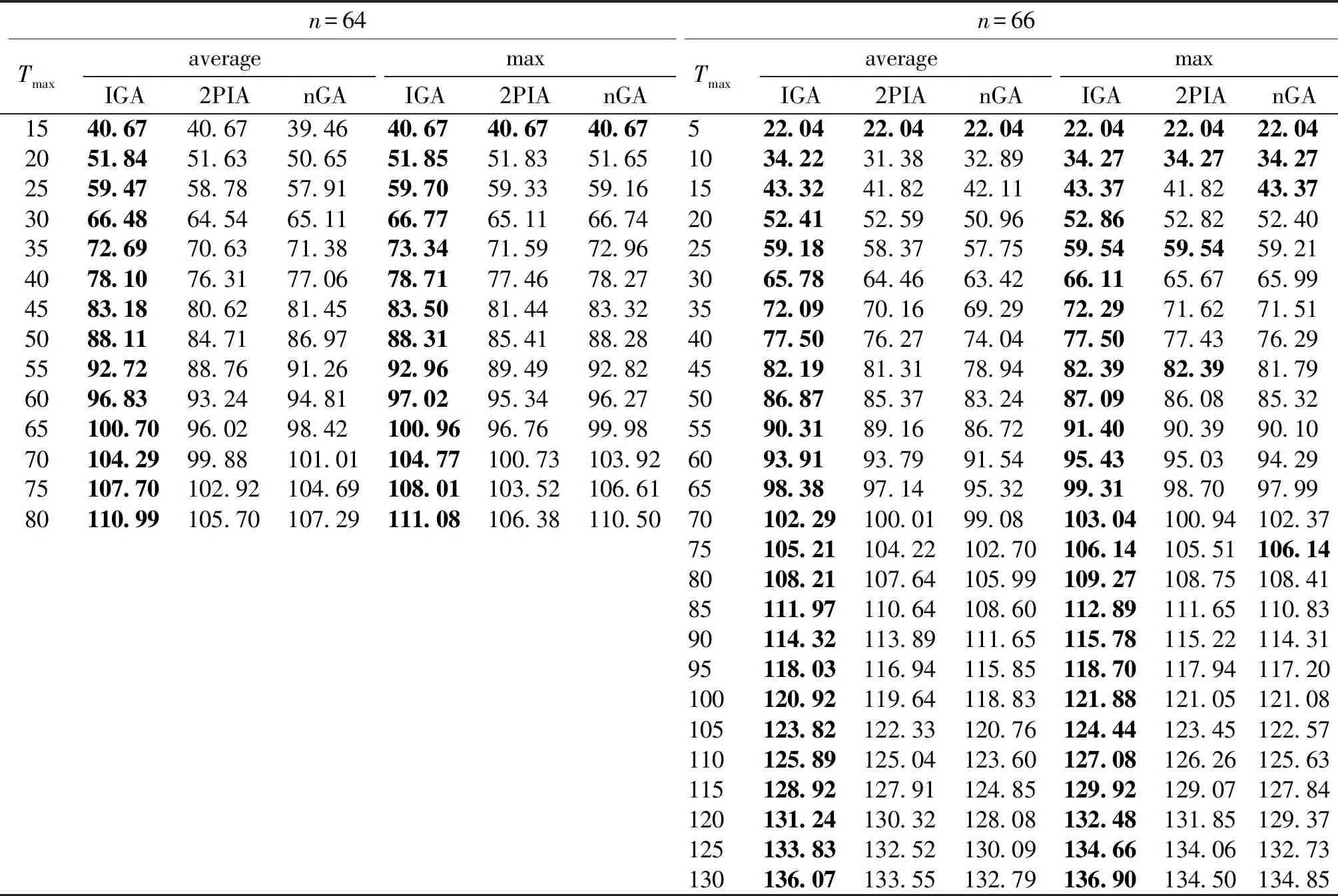
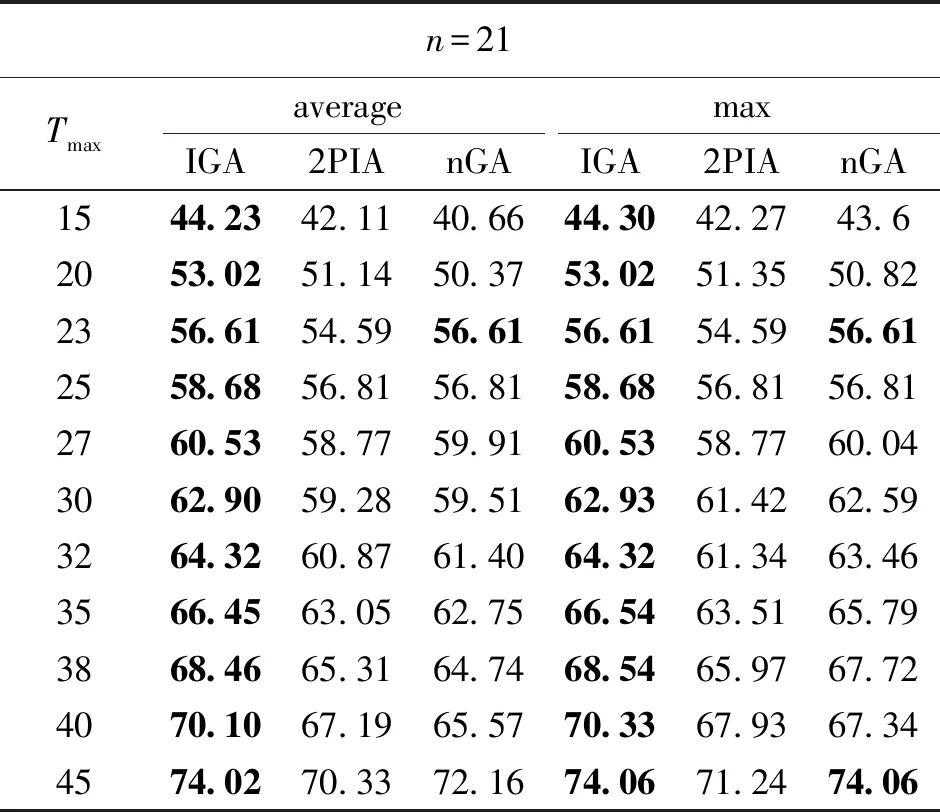
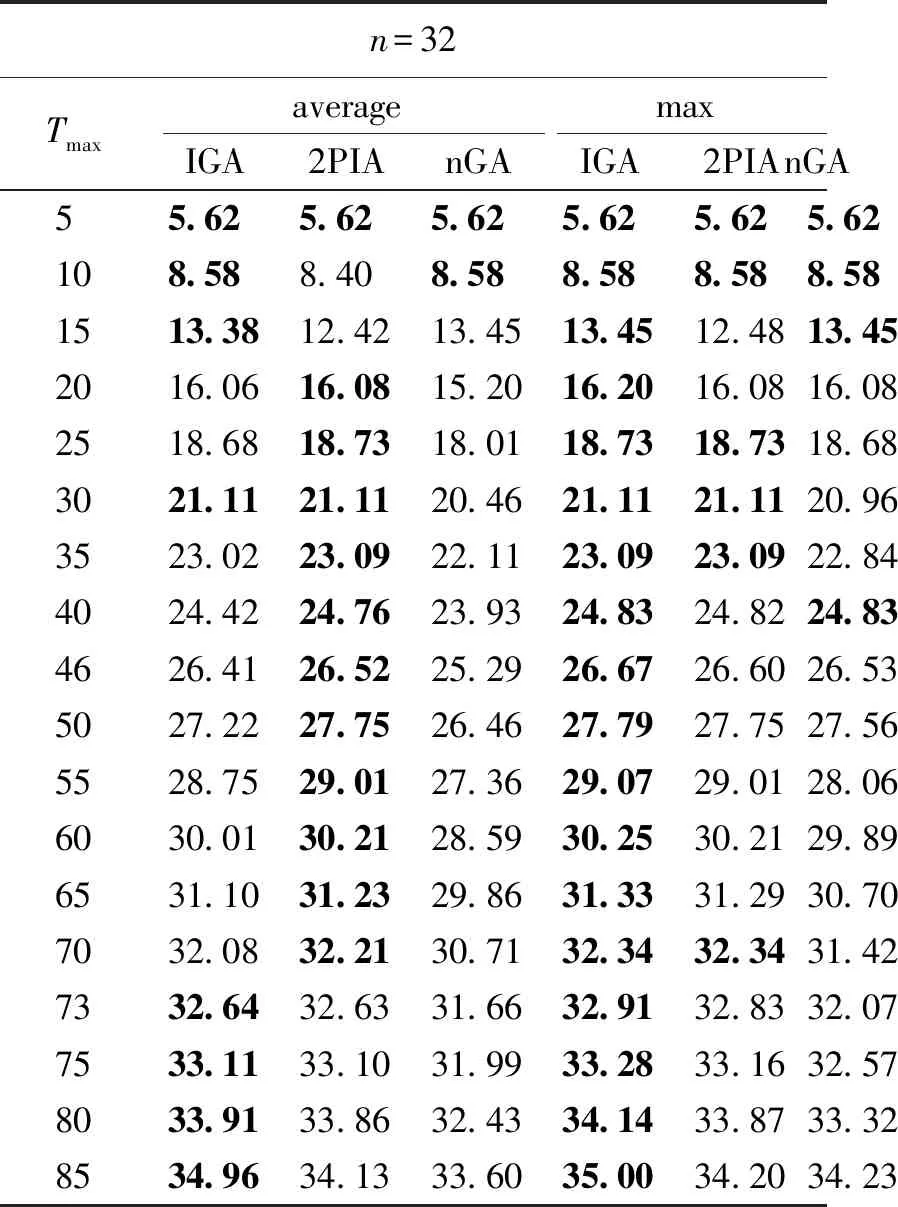
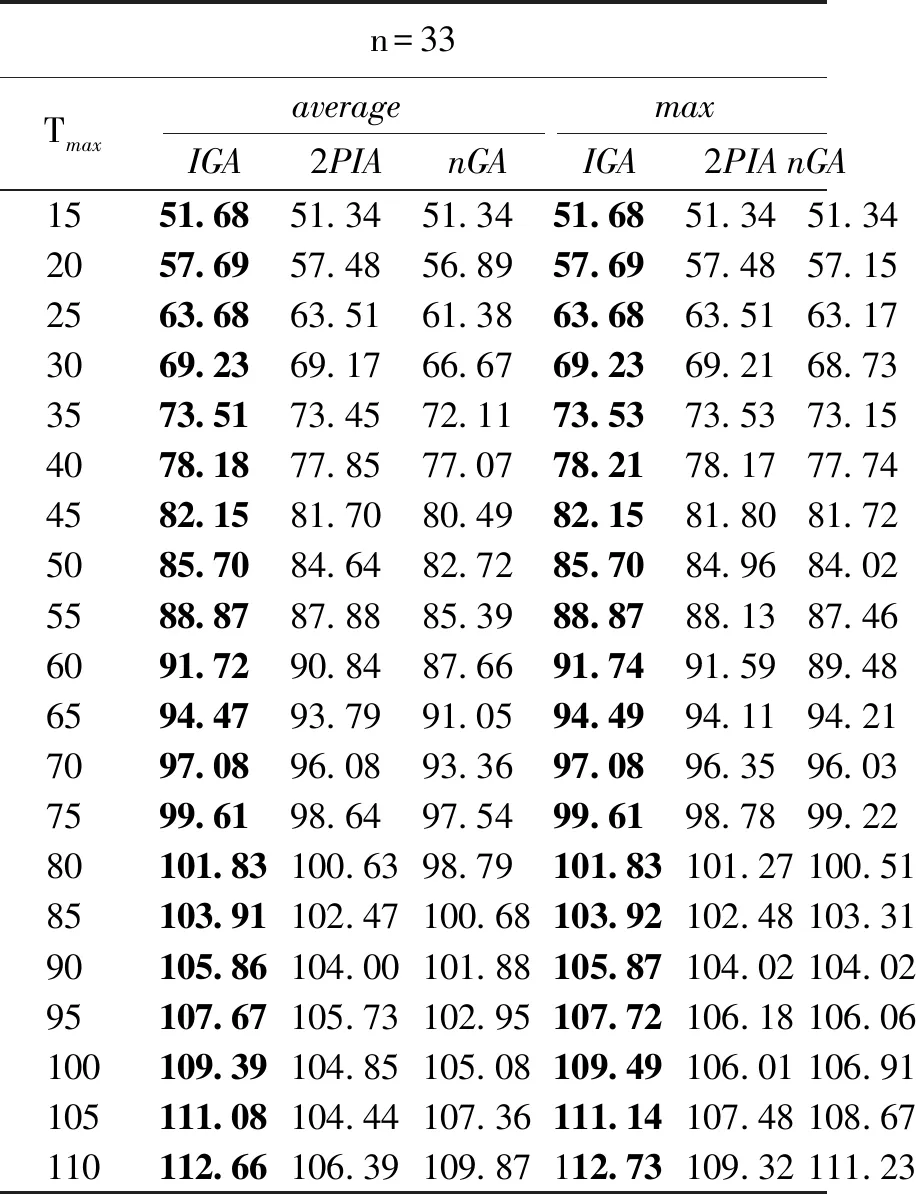
1) 选择算子.本文采用分组竞争的方式来选择个体.将种群大小Psize分为num组(num 2) 交叉算子.本文采用单点交叉的方式.首先随机两个个体作为父代,然后确定父代的共同基因(不包含起止基因)为交叉点集.若交叉点集不空,则以所有基因为交叉点进行交叉,并将适应值比父代大且可行的子代个体保存下来,否则不进行交叉操作. 3) 变异算子.本文应用和设计了6种变异算子.简单的插入和删除变异算子在随机选择的个体上执行,维持进化过程中种群的多样性,防止早熟;其他4种变异算子在多个分组竞争中优胜的个体上执行,加强优良个体的局部搜索能力,进一步改善解的质量.其中分组竞争的方式和选择算子操作一致.变异算子具体过程如下. a) 替换变异.用新基因替换染色体上的基因,并用替换后收益最高且可行的子代来更新父代. b) 逆转变异.逆序所有的基因片段,以减少个体长度[13],以便插入更多的基因片段,增加个体收益,如图2所示. c) 交换变异.调换任意两个基因的位置,并用操作后长度最短的个体来更新原染色体,如图3所示. d) 轮转变异.针对收益可变的问题特点,循环移动基因片段,对产生的所有新子代,保留可行且收益最佳的子代以更新父代,具体如图4所示. 图2 逆转操作Fig.2 Operation of reverse 图3 交换操作Fig.3 Operation of swap 图4 轮转操作Fig.4 Operation of turn 与GOP不同,GOPVP中点的收益可变,染色体基因的序列直接影响到个体的目标函数值.轮转操作更详细的例子如图5所示.每个点有两个类型的收益,且随时间线性下降,如图中f所示,最大时间限制Tmax为10.图中菱形表示起止点,圆形表示待访问点.假设目标函数中指数k为1,两个类型权重均为0.5. 图5 轮转操作例子Fig.5 Example of turn operator 在图5的示例中,图5(a)中可行解为source-d-a-b-c-destination,根据目标函数公式(1)计算,其总收益为46.5.图5(b)中可行解为source-a-b-c-d-destination,其总收益为59.5.通过轮转操作,可进一步提高解的质量. 3.1.1实验数据 本文采用3个经典算例集来验证算法的有效性,分别为Wang等[1]提出的GOP算例和Tsiligirides[14]、Chao等[15]提出的OP算例,将它们扩展成GOPVP实例,并分别命名为setW、setT和setC. setW算例(起止点相同)为中国东部27个城市,其位置坐标为城市对应的经纬度,每个城市间的距离根据经纬度计算.算例中,城市具有4个不同类型的评分.在现实应用中,不同的类型可以表示旅游规划中城市的各种旅游特色,也可以表示低温冷链物流中各种物资类别. setT和setC是两个经典的OP算例,其原始数据及改造数据被研究者们广泛应用.setT包含3个不同的点集,个数分别为21、32、33.setC算例包含两个不同的点集,个数分别为64、66.每个点集都有多个不同的Tmax.在setT和setC中,路径的起止点不同,点之间的距离采用欧氏距离.由于算例中每个点仅有一个类型的收益,因此本文扩展这两个数据:随机打乱点集收益值,形成新的收益序列.重复3次,构造多类型数据. 本文目前的实验中假设了各类型收益均随时间呈线性下降,其函数形式为fig(ti)=sig(0)-αti,i∈V,g=1,2,…,m,且fi1(ti)=fi2(ti)=…=fim(ti),其中:α=sig(0)/Tmax;sig(0)为点i在第g个类型上的初始收益.更一般性的收益下降函数有待进一步研究. 3.1.2对比方法 在3个不同的算例上,与本文提出的改进的遗传算法(improved genetic algorithm,IGA)对比的研究进展算法为nGA算法和2PIA算法. 1) nGA算法.Zabielski等[9]基于GA的OP求解算法,采用了锦标赛的选择算子,并综合采用了插入、删除和逆转的变异算子. 2) 2PIA算法.Silberholz等[5]提出的两参数迭代算法,采用了逆转、插入和删除的局部搜索操作. 3.1.3参数设置 对比方法采用原文参数设置.IGA的相关参数设置如下:迭代次数T为50,没有改善的迭代次数限制为5,种群大小Psize为50,选择操作中分组个数num为5组,交叉操作随机选择15对父代进行操作,变异操作中随机个体数占种群大小的10%,其中插入和删除变异概率都为0.5. 此外,本文以单位时间间隔分割最大时间限制Tmax(由于距离和时间转换简单,本文对测试实例中的边权耗费不做区分),并预先存储各结点在不同时刻的收益,以加速计算.为了消除各算法随机性带来的影响,本文将每个算法在各个数据上分别进行10次独立重复实验,取10次运行结果的最大值和均值进行比较,同时比较各算法求得结果的标准差,验证本算法的稳定性. 3.2.1setW 类似于文献[5],本文测试目标函数中5个不同的目标函数指数k分别为1,3,4,5,10,对不同的k值分别考虑5个不同的类型权重wv(0:[0.25,0.25,0.25,0.25],1:[1,0,0,0],2:[0,1,0,0],3:[0,0,1,0],4:[0,0,0,1]),Tmax均为5 000. 在25组测试实验中,本文分别比较了3个算法求得的目标函数均值和最大值,结果如表1所示.从表中可以看出,在最大值和均值上,文本的IGA算法全部都达到了最优值.setW的仿真实验表明,相比对比方法,在不同目标函数指数和类型属性权重组合下,仍能够保持较好的寻优求解优势,体现了较强的寻优能力. 3.2.2setT、setC 由于测试实例过多,对setT和setC,本文仅实验指数k为2,类型权重为(0.25,0.25,0.25,0.25)的目标函数.setT算例共有49组不同的实验,setC算例共有40组不同的实验.3种算法的求解结果比较分别如表2和表3~5所示,表中n为算例中点的个数,Tmax为最大时间限制.在数据集setT和setC上,同样比较各算法求解目标值的均值和最大值. 由表2和表3~5可知,本算法能适应不同点集大小和时间限制的组合,在大部分组合中,IGA求得的目标最大值和均值都取得了明显的优势.在均值比较上,当n=32时,2PIA取得了和本文算法相当的效果,且均优于nGA.在整个setT数据集的49个算例上,本文取得了39次最优结果,并且在setC上全部取得最优,远远超过2PIA和nGA.在最大值比较上,2PIA和nGA在setT仿真实验上都仅取得6个最优解,在setC上都仅取得5个最优解,而本文的IGA算法则全部达到了最优,进一步证明了改进算法的优越性. 表1 setW 算例实验结果Tab.1 Result of setW 表2 setC实验结果Tab.2 Result of setC 表3 setT实验结果Tab.3 Result of setT 3.2.3稳定性分析 为了验证IGA算法的稳定性,本文采用标准差作为评价指标进行比较,如表6所示,其中n为算例中点的个数.表中的结果为算法在该算例集不同实验方案标准差的平均值.从表中可以看出,在setW、setT和setC 3个算例集上,IGA求解结果的标准差都比较小,且均显著优于其他算法.在setW和setT上,IGA求解结果的标准差接近0,表明算法每次独立实验几乎都能找到最优解.从实验结果可知,与2PIA和nGA相比,IGA具有更好的稳定性. 表4 setT实验结果Tab.4 Result of setT 表5 setT实验结果Tab.5 Result of setT 表6 不同算法的标准差对比结果Tab.6 Comparison of standard deviation for different algorithms 考虑带有多类型和收益(价值等)随时间变化特点的实际应用场景,本文提出了一类收益可变泛化定向问题,并建立了相应的数学模型.设计了一种改进的遗传算法来解决该模型,采用分组竞争机制在全体种群中搜索优胜解,不仅保持了解的多样性,同时保持了解的优良性.再通过基于收益可变特点的变异算子,进一步加强了解的质量. 为了评估提出算法的有效性和稳定性,在3个扩展的数据集上进行测试.由仿真实验可知,提出的算法,相比于研究进展方法,能找到更优的可行解.同时由标准差分析可知,本算法具有更好的稳定性. 更多实际特征是接下来考虑的因素之一,如时间窗[12]和时间依赖[16]等.此外,对于大规模应用场景,进一步改进算法,快速求得高质量的可行解是下一步的研究工作.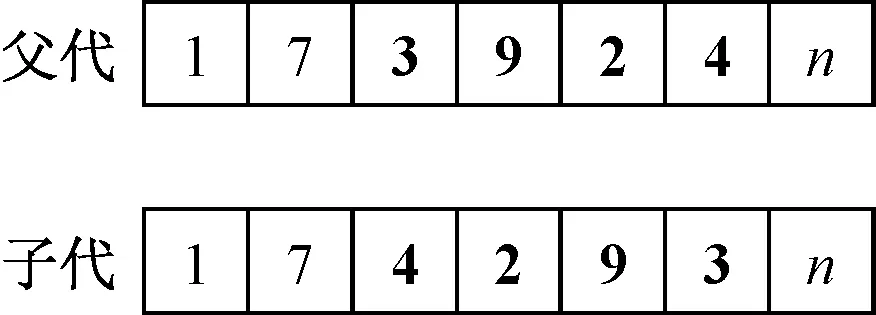
3 实验设置及结果分析
3.1 实验设置
3.2 实验结果及分析

4 结论
——基于人力资本传递机制
——基于子女数量基本确定的情形

