三相并网逆变器的混杂自动机模型分析
李冬辉, 郑宏宇, 姚乐乐
(天津大学 电气自动化与信息工程学院, 天津 300072)
并网逆变器(Grid Connected Inverter, GCI)作为太阳能等一些可再生能源发电系统与电网的接口,其性能直接影响到发电系统输出的电能质量.因此,针对逆变器的建模及其控制策略的研究已成为当下一个热点.
线性控制器在分析时均需通过平均化[1]、坐标变换或小信号线性化[2]等方法对系统进行近似线性化处理,在其近似处理的过程中会忽略系统的某些因素,故不能完整地体现出三相逆变器的动态特性.非线性控制的方法可以有效提高系统的动态性能[3-4],但在参数设计时较复杂,故传统控制器的局限性越来越大.
文献[5-6]中研究了混杂系统的建模及控制方法,虽然控制效果有所改善,但直接将传统控制方法引入到混杂模型中,并没有从根本上解决传统方法的固有缺陷.文献[7-10]中说明了切换系统在逆变器的控制器设计中应用越来越成熟,但是三相逆变器的动态性能仍有待改善.
文献[11-14]中利用Lyapunov函数对分段线性系统以及切换控制系统的控制器进行设计,并通过Lyapunov函数做稳定性分析.虽然Lyapunov稳定性分析法在控制系统中被广泛应用,但是构造Lyapunov函数时需要结合混杂模型,凭借经验试凑.本文在以上基础上提出了一种基于混杂自动机模型的三相逆变器改进控制策略.首先该策略从减小并网电流谐波含量的角度,对子系统转换边界以及开关模态的切换条件进行详细设计.然后将切换信号看作切换控制器,结合三相并网逆变器的混杂模型,对该切换控制器下的系统进行有限时间稳定性分析.最后通过Saber仿真,并搭建三相并网逆变器实验平台,对本文所提出的方法有效性进行验证.
1 三相逆变器的混杂自动机模型及其控制器设计
三相逆变器的拓扑结构如图1所示.该结构通过滤波电感L、电阻R与负载相连;直流侧母线电压为Udc;T1~T6为IGBT开关管;Sa1、Sb1和Sc1为上桥臂开关驱动信号,Sa2、Sb2和Sc2为下桥臂开关驱动信号;ea、eb和ec为电网电压,后面计算中也可用ua、ub和uc表示;iD为流入逆变器的电流;N为中性点.根据电路工作原理,定义三相逆变器中 IGBT 导通状态如下:
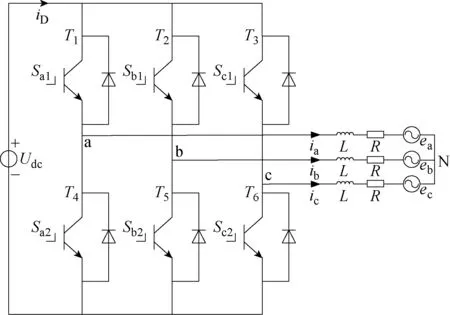
图1 三相逆变器Fig.1 Three-phase inverter
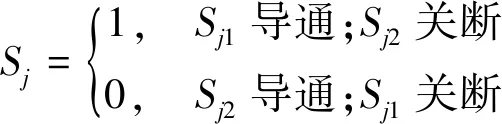
(1)
j=a,b,c
根据以上定义及三相逆变器拓扑结构可知其状态方程为
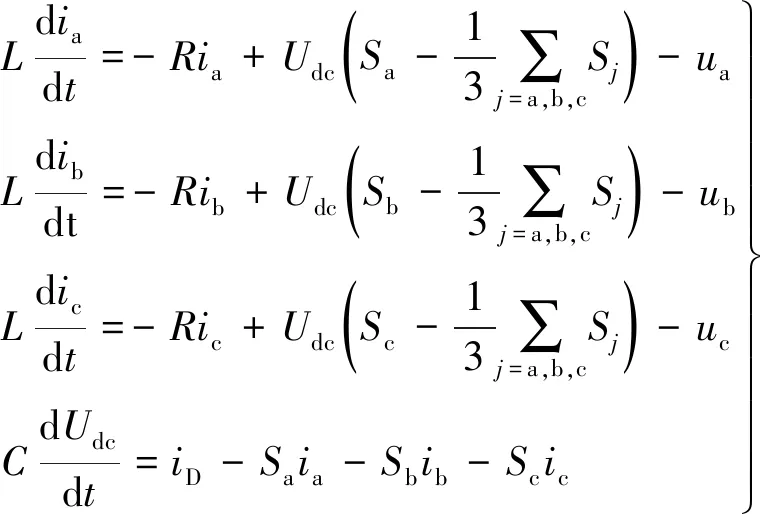
(2)
式中:Sa、Sb和Sc为逆变器开关函数;Sj为单极性二值开关逻辑函数,其含义同式(1);C为直流侧稳压电容.
混杂自动机理论是一种更侧重于分析混杂系统离散特性的建模与控制方法,是将计算机领域中的有限状态机方法引入到混杂系统的分析中而形成的.混杂自动机在设计完成并启动运行后,即可完全自动地工作,并得到期望的输出,而不需要外加激励.所以,从控制的角度看,混杂自动机模型的设计过程中,不仅包括被控对象,也包括其中的控制器.建立系统的混杂自动机模型的过程,本身也是混杂控制器的设计过程.在混杂自动机模型中,各个离散状态对应的状态方程表示被控对象;控制离散状态间转换的边界条件,即为系统的控制器.设计混杂控制器,即为设计合理的边界条件,控制子系统间转换的过程.
本文对于边界条件的设计所采取的切换事件并不是预先设计好的时间点,而是根据系统内部变量设计的切换事件,属于事件型控制器,因此可以实现对复杂系统的控制且能够达到更优的控制效果.
考虑到在进行模态切换时既能保证逆变器的输出电能质量又能有效减少开关器件的开通和关断次数,所以需要借助电压空间矢量调制的观点,将一个周期360°的范围划分为12个等宽度的30°子区间,每个子区间内电压的大小关系都是不一样的,然后再确定每一个子区间内部的具体工作过程.相比于6个子区间的控制策略,本文所提的改进控制策略可以更加精确地描述系统的切换过程以及系统内部的固有连续,从而获得更好的控制效果.
以0°~30° 为例,逆变器输出的电压关系为uc>ua>ub,可以保持b相对应桥臂的输出电压始终为低,即b相上桥臂始终关断,下桥臂始终导通,余下的4个开关器件发生切换,简化后此过程只有3种开关状态组合,即可完成电压转换的功能.所采用的开关状态开关序列为与SVPWM相同的开关序列表示法.
要确定控制切换的边界条件首先要确定每一种模态在切换过程中所持续的时间.同样以子区间 0°~30°为例说明其边界条件的求取.0°~30°子区间的3种开关序列模式为 VI、II 和 I,各个模态维持的时间分别为t1、t2和t3,根据各个模式下各开关器件的开断状态可得到相应的简化模型如图2所示.
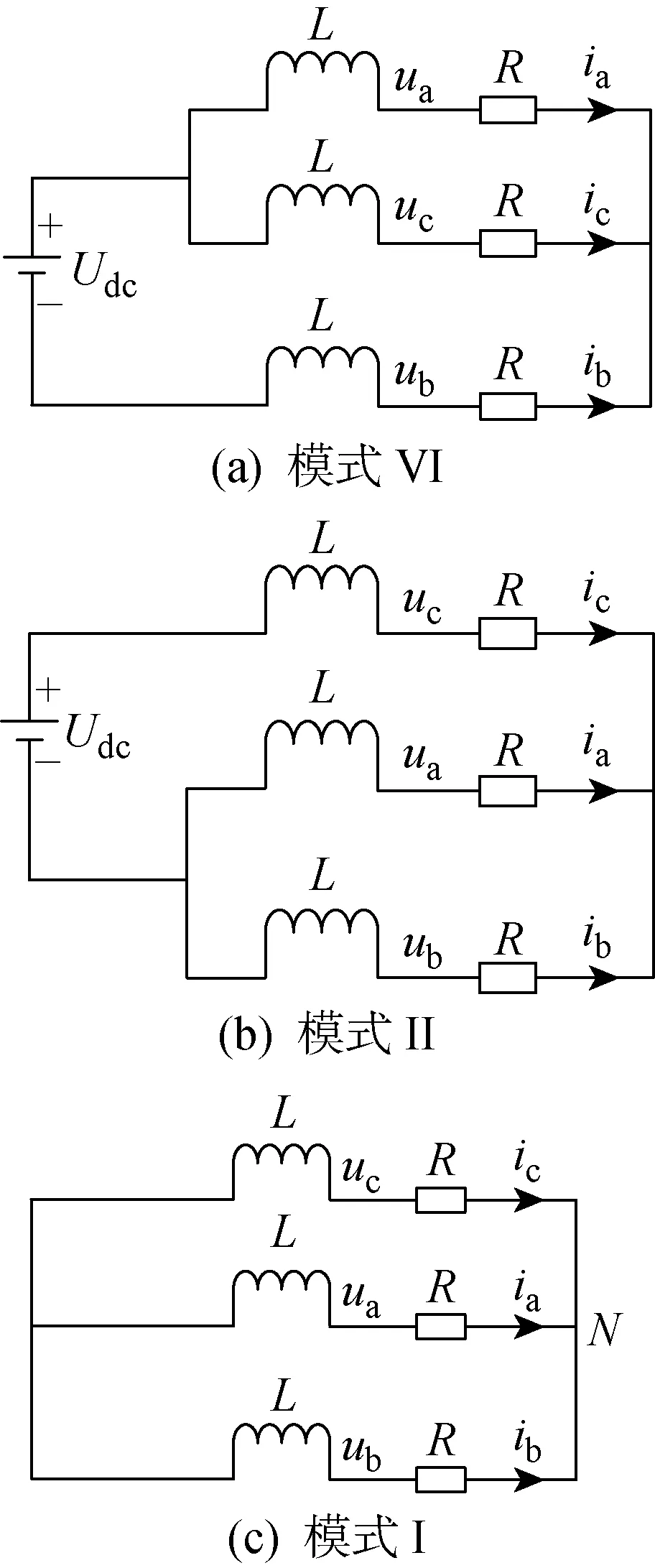
图2 简化电路结构Fig.2 Structure simplified circuit
按照图2所示电路结构模式可得如下对应状态方程:
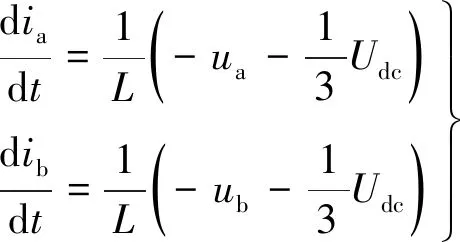
(3)
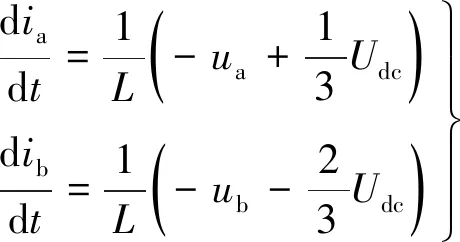
(4)
(5)
开关周期为微秒级,而每种开关模式约为1/3个开关周期,故各个开关模态中的电压ua、ub和uc可以近似不变,进一步可以认为在每个开关模态内,电感电流是线性变化的.因此,各个模态的电流近似变化量为
化简可得一个开关周期内电流的总波动值为
(9)
式中:ts=t1+t2+t3表示开关周期.一个开关周期的时间很短,可以近似地认为输出电流的变化量为零,故切换的时间点为
(10)
综上所述,可以求出0°~30°区间内的3个开关模态的具体转换边界条件为
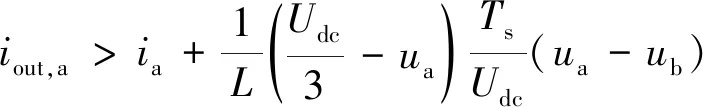
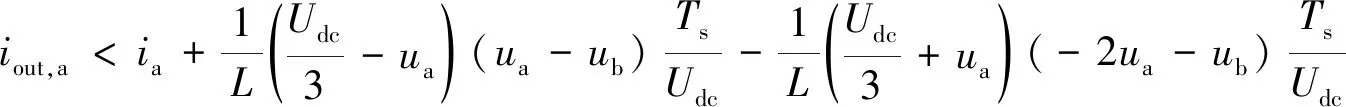
(3) 当iout,a 其中:ia表示a相参考电流;iout,a表示a相实际输出电流. 同理,可求出其余11个子区间的切换点及其切换模态,再结合各个区间内电压的大小关系及电流的变化情况便可求出相应的切换条件.这些切换条件即为切换信号,该信号就是三相逆变器混杂自动机模型下的控制器. 针对混杂系统的切换控制策略的稳定性分析,本文提出一种适用于混杂系统的有限时间稳定的方法,该方法无需事先给定混杂系统的切换顺序.有限时间稳定是指在某一给定的时间间隔内,对于给定的初始状态,系统的状态轨迹始终保持在某一给定的范围内.假定连续系统状态用x(t)表示,系统的系数矩阵用Ai表示,则连续时间切换系统的表达式为 (11) 切换信号σ(t)是指各个开关模态下等效电路之间的切换信号,是时间的分段常值函数,该信号依赖于时间t或由逆变器输入电流iD以及滤波电感电流ia~ic构成的状态x(t),或同时依赖于时间t和状态x(t). 考虑图1所示的三相逆变器,将式(2)所示模型用如下形式表示: (12) 式中:x∈Rn为系统状态向量,u∈Rm为系统的输入向量,可表示为如下形式: (13) (14) 系统输入向量可用下式表示为 u(t)=Kσ(t)x(t) (15) 式中:Kσ为反馈增益. (16) (17) 成立,则系统输入向量u(t)在满足式(15)的情况下,对于任意满足下面平均驻留时间条件的切换信号σ(t),可使三相逆变器在有限时间内稳定.过渡时间用τa表示,即 (18) 式中: 将式(2)按照式(12)进行变换后,其中x(t)和u(t)如式(13)和(14)所示,并将Sj的具体数值代入,从而得到式(12)中的Aσ(t)和Bσ(t),即 为了验证本文所提出的系统模型和控制策略的有效性及控制性能的优越性,将所提出的方法与传统的混杂模型控制器进行对比.在Saber仿真环境中搭建三相逆变器,并对该系统进行仿真验证.设光伏阵列输出的电压为DC 300 V,逆变器的滤波电感为8 mH,滤波电阻为20 Ω,响应周期为 0.02 s,电网电压峰值为150 V. 图3 逆变器输出动态波形及谐波分析Fig.3 Inverter output dynamic waveform and harmonic analysis 逆变器输出电网电压与并网电流波形、三相并网电流波形及其谐波分析如图3所示.图中,总谐波畸变率THD=0.56%.由图可知,稳态时采用改进后的控制策略可以得到三相对称的并网电流,且相对纹波较小;采用改进的增加子区间的方法可以使混杂自动机模型控制更加精确地描述三相逆变系统,有效降低输出并网电流的谐波含量,实现对并网电流与电网电压的同频同相控制.验证了所提出的改进方法的准确性与可行性. 图4所示为传统混杂模型控制下的电流波形以及对应的谐波分析图.图中,逆变器输出电流总谐波畸变率THD= 2.37%,远高于改进后的逆变器输出谐波含量. 由图3和4可知,本文所提出的方法有效提高了基波含量,使其近似等于三相并网电流值,高于传统混杂模型方法的基波含量(约等于8 A),并且可以有效降低高次谐波.因此,本文所提方法可以有效降低并网电流的谐波含量. 为了进一步验证本文所提出的方法可以很好地改善三相并网逆变器的动态特性,在输入直流电流变化时,逆变器输出波形如图5所示.由图可知,当三相并网逆变器输入直流电压突降且叠加小幅值交流电压时,逆变器输出a相电压也相对发生畸变,但在改进后的混杂模型控制下可以很快恢复正常,且在有小范围电压波动情况下,输出电压可以不受干扰. 图4 传统混杂模型a相并网电流及其THD分析图Fig.4 a-phase grid current and analysis on its THD in traditional hybrid model 图5 输入直流电压突变时输出a相电压波形Fig.5 a-phase output voltage waveform changes with the input DC voltage 综上所述,本文所提出的改进方法不仅具有良好的暂态稳态特性,有效降低输出电流的谐波含量;同时还具有较强的动态特性,当逆变器输入电压受到扰动干扰后可以快速达到稳定,抵消扰动. 为了更好地验证本文所提出的模型和控制方法的有效性和可行性,搭建了主要由PC机和TI公司32位定点TMS320F2812 DSP组成的三相逆变器实验平台.实验平台的主电路见图1,采用三菱公司的智能模块IPM-PS21869作为主电路的功率变换模块,实验系统参数与仿真模型参数一致.辅助电路中的交流电流检测模块采用HBC20LSP电流霍尔传感器检测逆变器的输出电流,其中电压与电流的关系为:u=2.5±2.0(i/IPN),IPN=20 A. 图6和7分别为本文所提方法和传统混杂模型下的逆变器输出电流波形和其THD分析图.由图6和7中的实验结果可以看出,改进后的混杂模型控制算法不仅可以很好地实现并网电流与电网电压的同频同相控制,而且可以有效减少逆变器输出并网电流的谐波含量. 图6 a相并网电流及其THD分析图Fig.6 a-phase grid current and analysis on grid current THD 图7 传统混杂模型并网电流及其THD分析图Fig.7 Three-phase grid current and analysis on THD 本文以典型的三相逆变器为基础,提出了相应的改进混杂自动机模型及其控制器.首先,为了减小并网电流的谐波畸变率,考察稳定工作状态下一个工频周期内的母线电压,采用增加子区间的方法,将其划分为12个子区间,并在每个子区间内设计8种开关模态的切换规则.这样得到的控制器较传统混杂模型的方法可以更加详细地描述逆变系统的动、稳态特性,有效减少逆变器输出的谐波含量从而实现良好的控制效果.然后,在三相逆变器混杂自动机模型的基础上提出一种新的混杂控制器稳定性分析的方法,即有限时间稳定法,并对系统进行了稳定性分析.最后,通过搭建三相逆变器的仿真平台与实验平台,对所提模型及其控制器进行仿真验证与实验验证.将仿真结果、实验结果与改进前的切换控制方法进行对比,本文所提出的方法可以降低并网电流的谐波畸变率,增加系统的抗干扰能力.2 稳定性分析
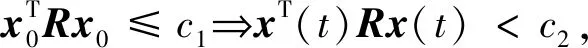
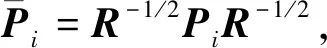
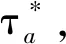
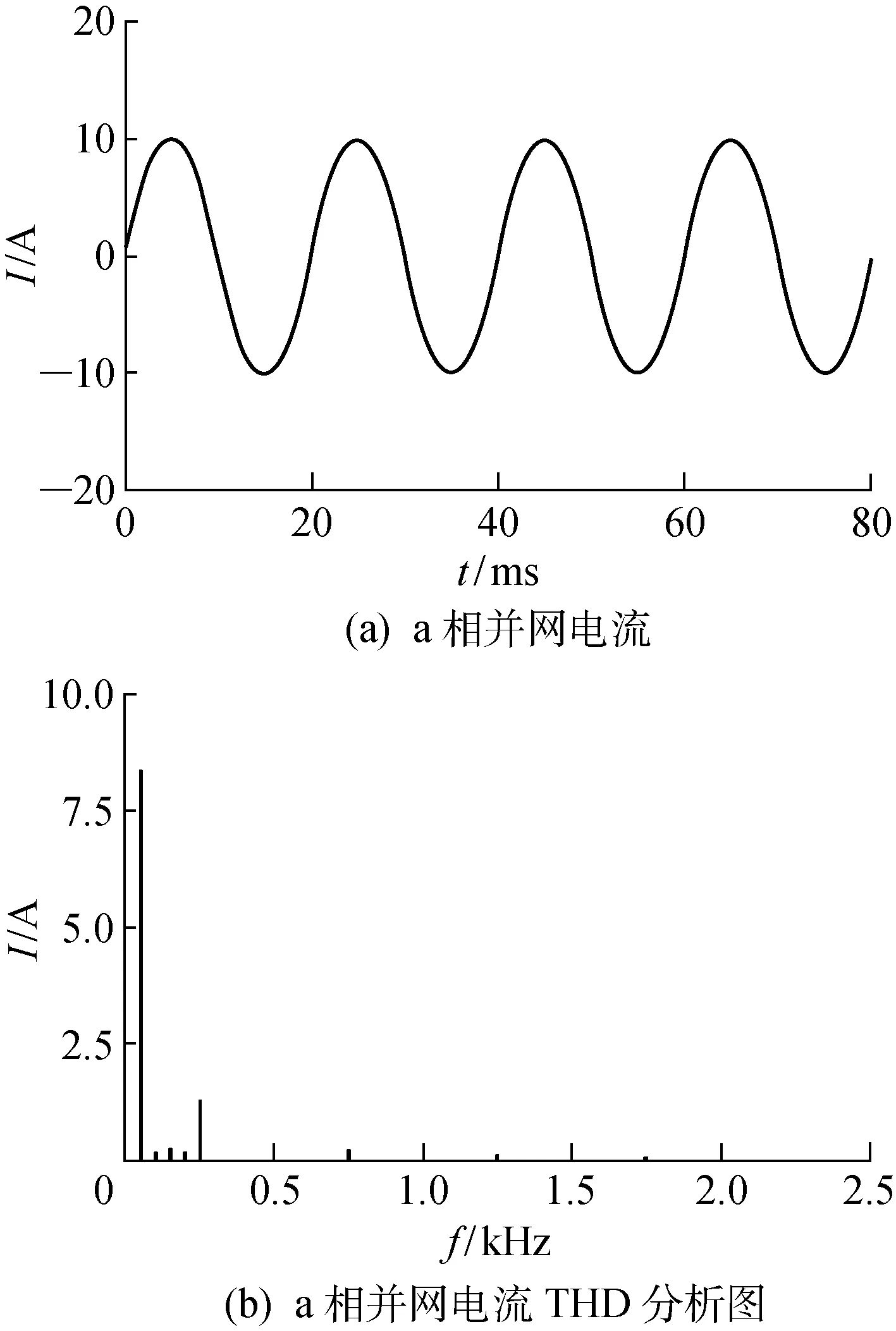
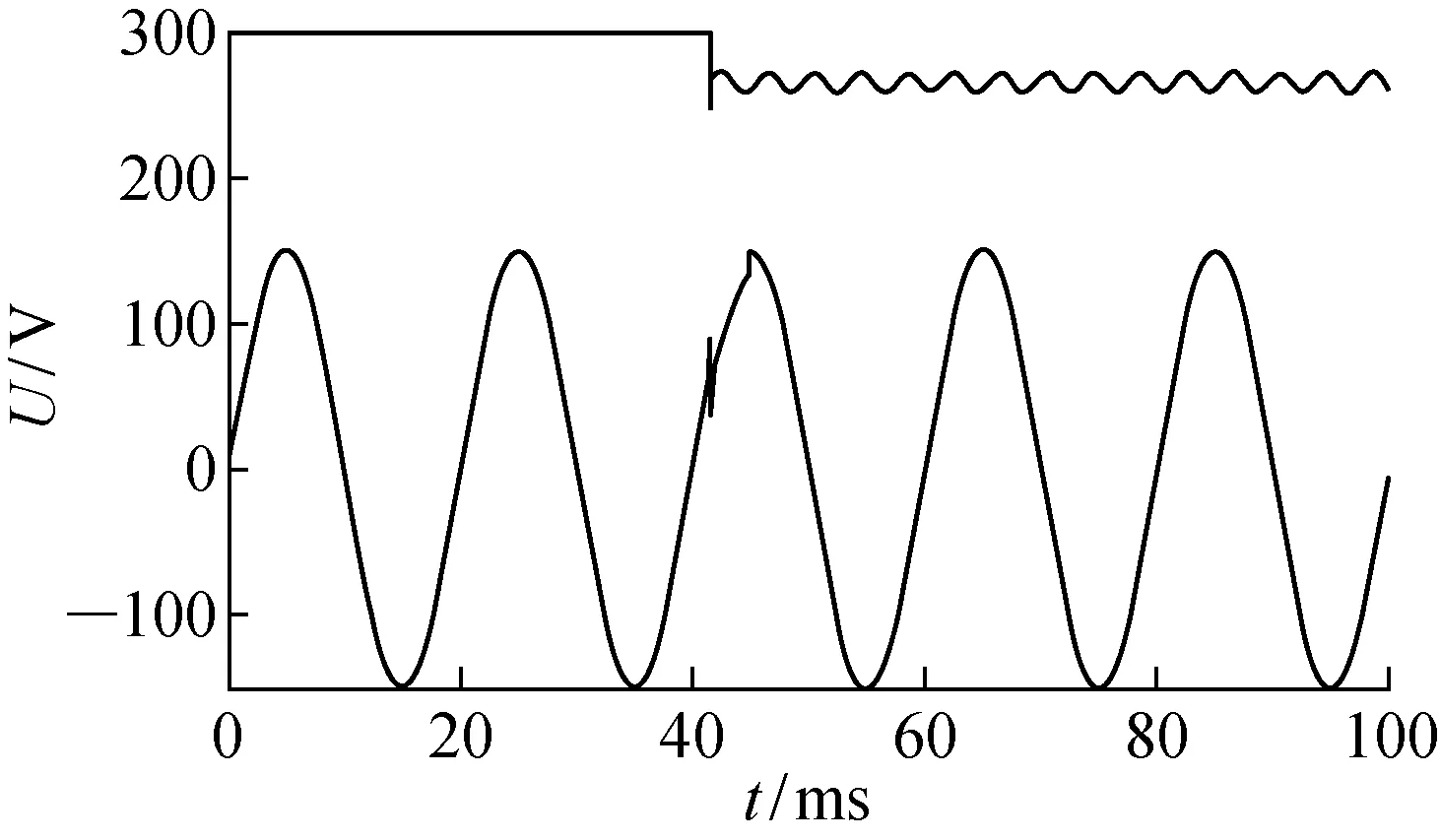
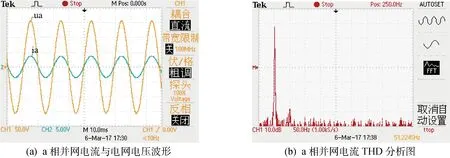
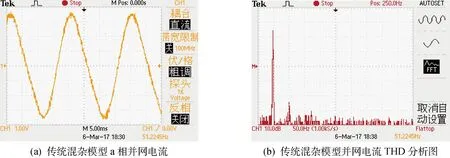
3 仿真与实验分析
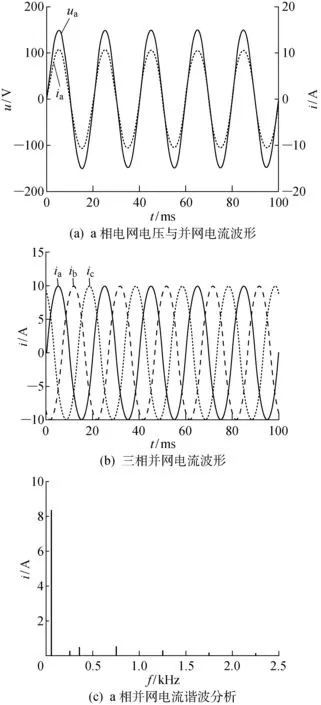
4 结语

