几类带空转移的n元伪加权自动机的关系*
赵路瑶,王海辉,李 平
(陕西师范大学数学与信息科学学院,陕西 西安 710119)
1 引言
自动机理论是计算机科学理论的基础。1961年,Schützenberger[1]提出了加权有穷自动机的概念。加权有穷自动机是经典的非确定型有穷自动机的状态转移函数、初始状态和接受状态都附加上权重而形成的一种有穷自动机,这些权值形成的代数结构一般为半环,得到了广泛研究[2 - 6]。1967年,Wee[7]提出了模糊有穷自动机的概念,开启了模糊自动机理论研究的历程。此后,又有学者相继提出了取值于完备正交模格的自动机[8,9]、取值于完备剩余格的有穷自动机[10,11]和取值于格序半群的模糊有穷自动机[12]。作为以上各种模型的扩展,2010年,Droste等[13]提出了取值于强双半群(伪半环)的自动机理论,且进行了深入研究[14,15]。伪半环是半环去掉分配律形成的代数结构,因此伪加权有穷自动机(取值于伪半环的加权有穷自动机)比取值于半环的加权有穷自动机更具一般性。
近一个世纪以来,自动机理论取得了长足发展,其广泛地应用于人工智能、文本处理、数字图像压缩、模型检测和模式识别等领域[16 - 21]。近来,我们发现自动机也可以应用于不确定性数据处理中,以解决不确定性数据世系分析中结果元组的概率计算问题[22,23]。然而解决此问题需要一个可以带有有限多个输入的自动机,以往的自动机概念都只带有一个输入或带有输入与输出2个信息,因此本文提出n元伪加权有穷自动机(带有n个有限输入字符集的伪加权有穷自动机)、分明型n元伪加权有穷自动机(初始状态与状态转移函数均是分明的n元伪加权有穷自动机)与确定型n元伪加权有穷自动机(初始状态与状态转移函数均是确定的n元伪加权有穷自动机)的概念。
在经典的有穷自动机理论中,带空转移的非确定型有穷自动机、非确定型有穷自动机与确定型有穷自动机是等价的[24,25]。在基于格序半群的模糊自动机理论中,除初始状态与接受状态均是分明的非确定型格值自动机以外,其他类型的非确定型格值自动机与带空转移的非确定型格值自动机均是等价的[26],而非确定型格值自动机与确定型格值自动机并不是等价的[12]。由格序半群和半环的代数性质可知,这些结论推广到取值于半环上的加权自动机依然成立。此外,在已知确定型加权自动机与非确定型加权自动机并不等价的前提下,文献[27]提出了状态转移函数是分明的加权自动机、带空转移的状态转移函数是分明的加权自动机的概念,并证明了以上二者是等价的,且它们与确定型加权自动机也是等价的。
然而由于伪半环未必满足分配律,以上结论并不能直接推广到伪加权有穷自动机中,并且到目前为止还没有文献直接讨论伪加权有穷自动机与带空转移的伪加权有穷自动机之间的等价性关系。因此,本文以n元伪加权有穷自动机为基础,根据状态转移函数在每个字符集上是否带空转移,将n元伪加权有穷自动机与分明型n元伪加权有穷自动机分为4类:带r-型空转移的n元伪加权有穷自动机、带空转移的n元伪加权有穷自动机、带r-型空转移的分明型n元伪加权有穷自动机和带空转移的分明型n元伪加权有穷自动机,并研究了上述几种类型的自动机之间的关系,讨论了状态转移函数在每个字符集上是否带空转移对其接受语言的影响,进一步完善了伪加权有穷自动机理论。
2 预备知识
首先回顾一下伪半环的概念及其相关结论。





注1在文献[15]中,伪半环又叫做强双半群。

例1[15]易验证下面的代数结构都是伪半环:
(1)(N,+,×,0,1)、(R,+,×,0,1)与([0,1],max,×,0,1)都是伪半环。其中,(N,+,×,0,1),(R,+,×,0,1)是交换且分配的,([0,1],max,×,0,1)是交换且加幂等的。
(2)格序半群是伪半环。同时,它们也是加幂等且分配的。
(3)格、完备格、完备正交模格和完备分配格都是伪半环。其中,格、完备格、完备正交模格、完备分配格均是交换、加幂等且乘幂等的。此外,完备分配格还是分配的。
3 n元伪加权有穷自动机及其识别的语言
本节给出n元伪加权有穷自动机、分明型n元伪加权有穷自动机和确定型n元伪加权有穷自动机的概念,并分别给出它们所识别的语言的定义。下面先回顾一下伪加权有穷自动机的定义。
定义2[15]伪加权有穷自动机PA(Pseudo weighted Automata)是一个五元组A=(Q,Σ,δ,I,F),其中,
(1)Q为有限状态集,Σ为有限输入字符集;


令Σ*表示Σ关于连接运算生成的自由幺半群,ε是其单位元。对任意θ∈Σ*,|θ|表示θ的长度,即字符的个数,特别地,|ε|=0。

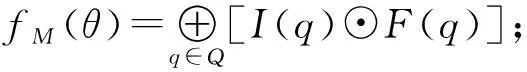

定义4n元伪加权有穷自动机(n-PA)是一个n+4元组M=(Q,Σ1,…,Σn,δ,I,F),其中,
(1)Q,I,F的意义同定义1;
(2)Σi为有限字符集,i=1,…,n;


若存在i,j,使得|θi|≠|θj|,则fM(θ1,…,θn) =0;
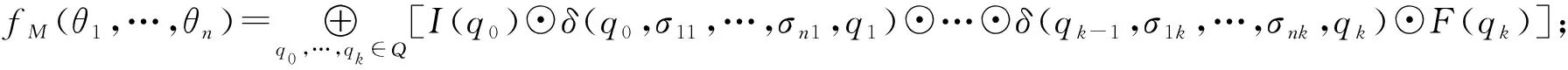
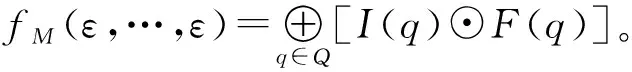

显然,当n=1时,n元伪加权有穷自动机即为伪加权有穷自动机。
定义5设M=(Q,Σ1,…,Σn,δ,I,F)是一个n-PA,若I={q0},δ:Q×Σ1×…×Σn→2Q,则称M为分明型n元伪加权有穷自动机n-CPA(n-ary Crisp Pseudo weighted Automata)。

若|θ1|=…=|θn|=0,即θ1=…=θn=ε,则δ*(q,θ1,…,θn)={q};
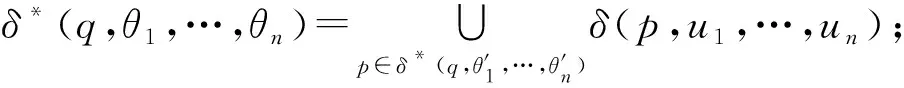
否则,δ*(q,θ1,…,θn)无定义。


定义6设M=(Q,Σ1,…,Σn,δ,I,F)是一个n-PA,若I={q0},δ:Q×Σ1×…×Σn→Q,则称M是一个确定型n元伪加权有穷自动机n-DPA(n-ary Deterministic PA)。

若|θ1|=…=|θn|=0,即θ1=…=θn=ε,则δ*(q,θ1,…,θn)=q;
若|θ1|=…=|θn|>0,不妨设θ1=θ′1u1,…,θn=θ′nun,则δ*(q,θ1,…,θn) =δ(δ*(q,θ′1,…,θ′n),u1,…,un);
否则,δ*(q,θ1,…,θn)无定义。

fM(θ1,…,θn)=
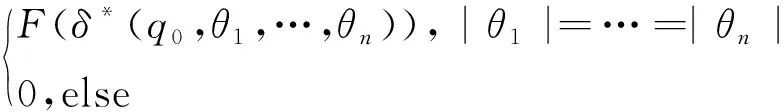

为方便起见,若I={q0},那么记M=(Q,Σ1,…,Σn,δ,q0,F)。
注3设Σ1,…,Σn是非空有限字符集,则由文献[27]中的定理4.1与文献[12]中的定理3.3可推出L(n-DPA,Σ1,…,Σn)=L(n-CPA,Σ1,…,Σn)L(n-PA,Σ1,…,Σn)。即n-DPAs与n-CPAs是等价的,但与n-PAs并不是等价的。称2个自动机是等价的是指它们所接受的语言类型是相同的。
4 带r-型空转移的n元伪加权有穷自动机及其识别的语言
本节将根据状态转移函数在每个字符集上是否带空转移,将n元伪加权有穷自动机进一步分类,给出它们分别接受语言的定义并讨论它们之间的关系。
定义7带r-型空转移的n元伪加权有穷自动机(n-rEPA)是一个n+4元组:
其中,
(1)Q,I,F的意义同定义2;
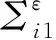

为给出M接受语言的定义,给出以下符号和概念。

又令PM=EM∪{π|π=e1e2…em(m≥2),ei∈EM,i=1,…,m,且π满足n(ei)=c(ei+1),i=1,…,m-1}。那么对任意π∈PM,称π是M的一条路径。例如,π1=(q1,ε,σ2,…,σn,q2)与π2=(q0,ε,σ2,…,σn,q1)(q1,σ1,…,σn-1,ε,q2)是M的2条路径,而π3=(q0,ε,σ2,…,σn,q1)(q2,σ1,…,σn-1,ε,q3)并不是M的路径。


当θ1,…,θn不全为ε时,

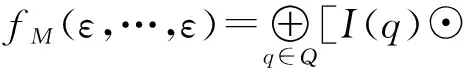

此外,注意到,对于一个n-PAN=(Q,Σ1,…,Σn,δ,I,F),其接受的语言具有等价形式:

当θ1,…,θn不全为ε时,
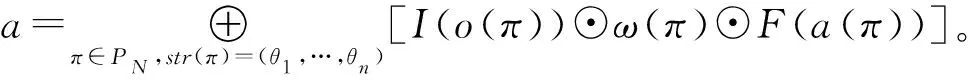
由此可见,n-PA是一个特殊的n-rEPA。
定义8带空转移的n元伪加权有穷自动机(n-EPA)是一个n+4元组:
其中,
(1)Q,I,F的意义同定义1;





定理1设Σ1,…,Σn是非空有限字符集,则L(n-PA,Σ1×…×Σn)L(n-rEPA,Σ1×…××…××…×Σn),其中,{i1,…,ir}是{1,…,n}的任意一个子序列。
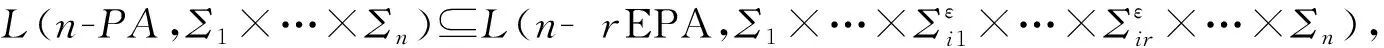

δ1(q,u1,…,un,p)=

构造过程如图1所示。

Figure 1 n-rEPA M图1 n-rEPA M

□

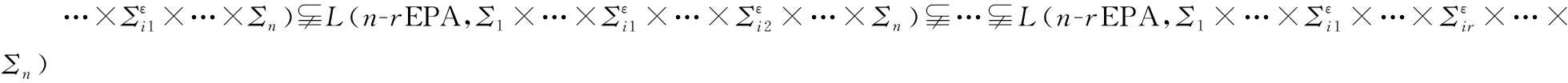

□
由定理1和定理2可得以下推论。
推论1设Σ1,…,Σn是非空有限字符集,则L(n-PA,Σ1×…×Σn)L(n-rEPA,其中,{i1,…,ir}是{1,…,n}的任意一个真子序列。
由以上定理与推论可知,n-PAs、n-rEPAs与n-EPAs三者均不是等价的。
下面介绍带r-型空转移的分明型n元伪加权有穷自动机的定义。

类似于定义7,首先给出以下概念。

又令PM=EM∪{π|π=e1e2…em(m≥2),ei∈EM,i=1,…,m,且π满足c(ei+1)∈δ(ei),i=1,…,m-1}。那么对任意π∈PM,称π是M的一条路径。例如,若δ(q1,σ1,…,σn)={q2},δ(q2,σ1,…,σn)={q3},则π1=(q1,σ1,…,σn)与π2=(q1,σ1,…,σn)(q2,σ1,…,σn)是M的2条路径,而π3=(q2,σ1,…,σn)(q1,σ1,…,σn)并不是M的路径。
对任意π=e1…em(m≥2)∈P(M),记o(π)=c(e1)为π的开始状态,a(π)=δ(em)为π的终止状态。又假设e1=(q1,σ11,…,σn1),e2=(q2,σ12,…,σn2),…,em=(qm,σ1m,…,σnm),则定义str(π)=(σ11σ12…σ1m,…,σn1σn2…σnm)。

当θ1,…,θn不全为ε时,

当θ1=…=θn=ε时,fM(θ1,…,θn)=F(q0)。





定理3的证明类似于定理1的,此处不再具体给出。

证明由n-rECPA和n-ECPA的定义可知定理显然成立。
□
由定理3与定理4可得如下推论:

由以上定理与推论可知,n-CPAs、n-rEPAs和n-EPAs三者是不等价的。然而,下面将证明存在一类特殊的n-EPAs,其与n-CPAs是等价的。





(i)q02=q01;

(iii)δ2:Q×Σ1×…×Σn→2Q,∀q∈Q,σ1∈Σ1,…,σn∈Σn,δ2(q,σ1,…,σn)={p|p∈a(π),π∈PM1,o(π)=q,str(π)=(σ1,…,σn)}。

(1)若存在π2∈PM2,满足str(π2)=(θ1,…,θn),则一定有|θ1|=…=|θn|,那么:
①当|θ1|=…=|θn|>0时,有:
fM2(θ1,…,θn)=
(1)
由(iii)可知,对任意的π∈PM2,且o(π)=q,str(π)=(θ1,…,θn),都存在一个π′∈PM1使得o(π′)=q,str(π′)=(θ1,…,θn),且a(π′)=a(π)。反之亦然。从而式(1)转变为式(2)所示:
(2)
又当π′2,π1∈PM1,o(π1)=q,q∈a(π′2)时,有π′2π1∈PM1,所以,式(2)转变为式(3)所示:
(3)
(2)否则,fM2(θ1,…,θn)=0=fM1(θ1,…,θn)。

□
以上定理说明,即使n-ECPAs与n-CPAs并不是等价的,但却有n-PECPAs与n-CPAs是等价的。
此外,由文献[27]中的定理4.2可以推出,当n=1时,n-ECPAs与n-CPAs是等价的。由此也可以看出,状态转移函数在每个字符集上是否带空转移对n元伪加权有穷自动机接受语言的影响不同于其对伪加权有穷自动机的影响。
5 结束语
本文以不确定性数据世系分析中结果元组的概率计算为应用背景,引入了n元伪加权有穷自动机(n-PA)、带r-型空转移的n元伪加权有穷自动机(n-rEPA)、带空转移的n元伪加权有穷自动机(n-ECPA)、分明型n元伪加权有穷自动机(n-CPA)、带r-型空转移的分明型n元伪加权有穷自动机(n-rECPA)、带空转移的分明型n元伪加权有穷自动机(n-ECPA)、确定型n元伪加权有穷自动机(n-DPA)与一个特殊的带空转移的分明型n元伪加权有穷自动机(n-PECPA)及其对应语言的概念,探究了以上自动机之间的等价性关系,并得到以下结论:

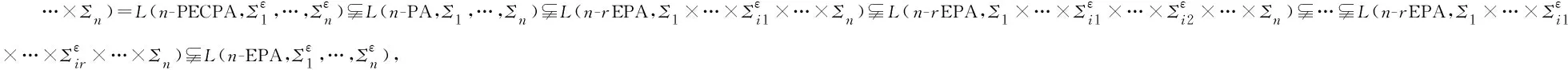
以上结论说明,状态转移函数在每个字符集上是否带空转移对n元伪加权有穷自动机接受的语言有着重要的影响,且不同于其对伪加权有穷自动机的影响。本文完善了伪加权有穷自动机理论,并为n元伪加权有穷自动机在不确定性数据处理中的应用奠定了理论基础。下一步的工作将以本文研究为基础探究n元伪加权有穷自动机在不确定性数据处理方面的具体应用。

