针对隐藏Web数据库的Skyline查询方法研究*
李征宇,李 贵,曹科研
1.东北大学 计算机科学与工程学院,沈阳 110004
2.沈阳建筑大学 信息与控制工程学院,沈阳 110168
1 引言
近年来,数据库Skyline 查询方法[1-4]得到了广泛的研究。Skyline 查询结果也被应用到多目标决策、top-k查询[5-6]、近邻搜索(nearest neighbor search)、凸包问题,以及基于用户偏好查询等众多的领域中。例如,利用事先计算的Skyline 可以有效解决基于属性排序的top-1查询问题,文献[5]利用基于Skyline扩展的K-skyband可以有效解决top-k(k≤K)查询问题。
随着Web 应用和Web 数据源的迅速增长,通过Web查询接口来获取服务端“隐藏”的数据库Skyline已成为Web数据挖掘领域的一个研究热点。通过获取隐藏Web数据库的Skyline元组可以支持众多基于Web的第三方应用,比如在Web信息集成中,通过获取多个隐藏Web 数据库的Skyline 元组,可以有效地解决满足用户偏好的top-k查询和推荐问题。通过top-k查询接口来获取服务器端“隐藏”数据库的Skyline 面临着诸多挑战,其中主要包括:(1)受top-k查询限制,每次查询结果最多返回满足条件的k个元组;(2)用户选择的查询条件受到Web接口类型和属性类型的限制;(3)用户端查询次数受到Web服务器的限制等。基于这些挑战,如何通过最少的查询次数获取服务端隐藏Web数据库的Skyline的元组成为解决问题的关键,目前实现方法有两种:一是通过Web 查询接口获取服务端隐藏Web 数据库的所有元组,然后在本地生成数据库的Skyline,这种方式的查询代价往往很高,同时受到Web 服务端查询次数的限制;二是通过设计合理的查询分解算法和对应的查询条件,通过Web 查询接口以较少的查询次数来获取服务端隐藏Web数据库的Skyline。文中针对第二种实现方法进行研究,主要贡献如下:
利用平行坐标系分析Skyline元组折线的相交性质;在定义相交元组查询分解树和证明查全性的基础上提出了Web隐藏数据库的Skyline元组的启发式求解方法;并依据Web 接口类型提出了基于混合属性条件范围的隐藏Web 数据库Skyline 元组求解算法;采用离线和在线数据集进行了算法的实验验证,通过理论分析和实验结果表明文中提出的算法在查询代价和查询效率方面都优于目前现有的方法。
2 相关研究
Skyline 的概念最初是由Borzsony、Kossmann 等人在文献[7]提出,随后研究者基于不同的背景进行了大量的研究工作,其中文献[8-10]利用索引和预排序技术提出了在线和渐进式的Skyline计算方法。文献[1]研究以支配分数作为度量,设计了基于表扫描的RSTS(ranked Skyline with table scan)算法来获取海量数据上有效top-kSkyline 的查询结果。文献[2]在交互式多用户的场景下,研究通过用户交互动态调节用户权重,设定满意度度量,以确定满意度最大的Skyline 候选集。文献[3]利用Voronoi 图解决静态和动态障碍环境中Skyline查询的问题。文献[4]在数据更新频繁时,研究基于时序支配的数据过滤方法,并提出了基于滑动窗口的ρ-支配轮廓查询算法。文献[5]研究了基于K-skyband的top-k查询算法,文献[6]研究了top-krepresentative Skylines 问题。文献[7-9]分别研究了基于流数据、偏序关系、不确定数据和成组技术的Skyline 计算方法。文献[11]研究了P2P 网络下不确定数据top-k的近似解法,通过引入Quad-tree 索引,分别根据局部和全局top-k间的关系,以及Skyline和top-k的关系,确定上下界实现空间剪枝,最后通过采样验证候选集。上述文献与Web 数据库Skyline有关的研究主要体现在top-k查询方面。文献[12]关注的是数据流上动态轮廓查询处理,动态轮廓查询是Skyline 查询的一个重要变种,目标对于一个给定的查询点q,返回在维度上最接近q的所有点。文献[13]针对Deep Web查询失效问题,提出了基于top-k和Skyline 的查询结果过滤方法和基于属性重要程度和数据源关系图的渐进式查询策略。文献[14]针对Deep Web集成查询中进行的数据抽样必须具备先验知识的问题,提出了ANS(adaptive neighborhood sampling)和TPS(two phase adaptive sampling)两种免先验知识的采样方法,以适用Web 隐藏数据库的集成查询。文献[15]研究了Deep Web数据集成的查询松弛策略,利用全局数据源关系图DRG(global database relationship graph)进行松弛查询,分别用Skyline、top-k方法筛选和排序结果集。文献[16]针对目标属性分属不同站点的情况,研究了渐进式分布Skyline 方法PDS(progressive distributed Skylining),以支持不同类型的Skyline查询和允许用户监督指导查询。文献[17-18]分别定义了优先和频繁Skyline点,并分别运用Skyline优先级和Skyline频繁度这两个新的度量来降低Skyline 候选集的规模,达到提升k-regret算法的目的。
然而,目前针对隐藏Web 数据库Skyline 的研究较少,文献[19]在预知Web数据库查询排名函数和获取所有排序元组的条件下,研究了从多个Web 数据库获取Skyline 计算方法。文献[20]提出了一种基于Web查询接口类型和属性类别的混合查询Skyline算法,但查询代价高,有些情况会超出爬取整个Web数据库的代价。
3 Skyline相关概念及性质
3.1 相关概念
隐藏Web 数据库是指Web 服务器端的数据库,用户对其查询只能通过Web查询接口(top-k查询)获得满足条件的部分元组记录。
假设隐藏Web数据库D具有n个元组,每个元组t有m个属性,分别记为A1,A2,…,Am。属性Ai的值域表示为Dom(Ai),属性值表示为t[Ai]∈Dom(Ai)∪{NULL}(1 ≤i≤m)[15]。
Web 查询接口依据隐藏Web 数据库的属性类型(数值型和分类型)可分为:范围查询、分类查询和混合查询。其中,范围查询基于数值属性指定范围条件的查询,包括单端范围查询(如价格<300)和双端范围查询(200<价格<300);分类查询是指基于分类属性取一个或多个具体值的条件查询;混合查询是指既包括数值属性的范围查询又包括分类属性的分类查询。
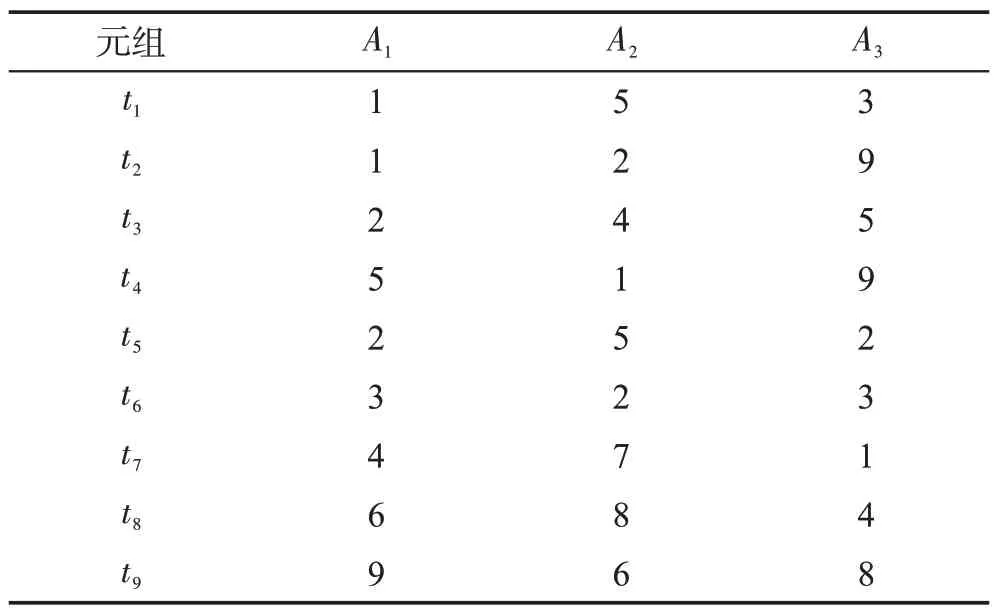
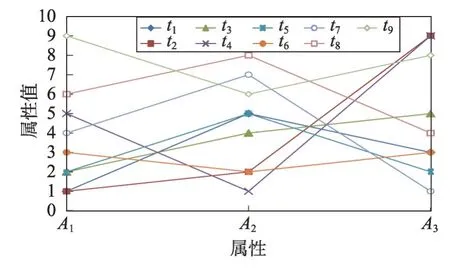
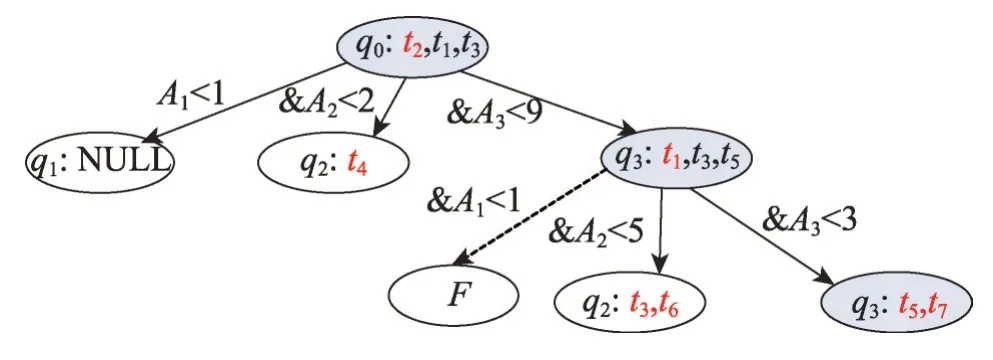
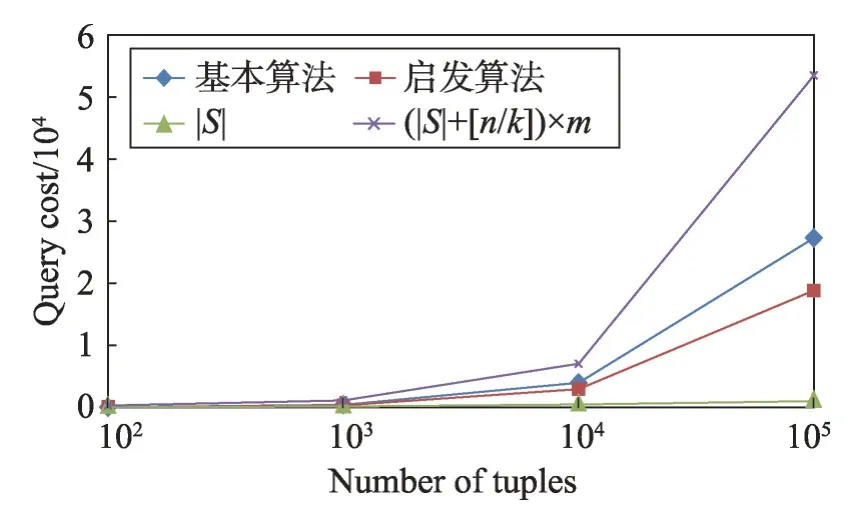
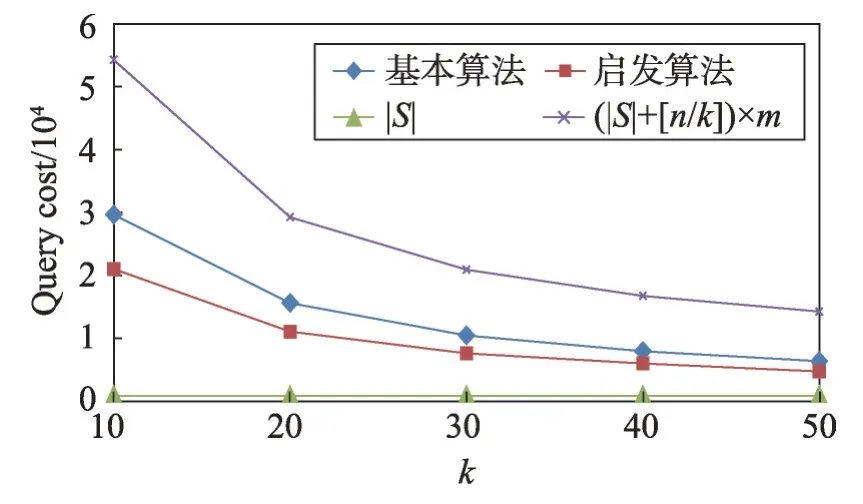
定义1(属性优先关系)数据库元组的属性按其重要程度进行排序,原则是重要的属性排在前面,次要的属性排在后面,对于属性序列{A1,A2,…,Ai-1,Ai,…,Am}来说,Ai-1优先Ai,记为Ai-1 定义2(元组支配关系)两个元组ti和tj,如果对于任一属性Ak(1 ≤k≤m),都存在ti[Ak]≤tj[Ak],则元组ti支配tj,元组ti和tj具有支配关系。否则,元组ti和tj是非支配关系。 定义3(元组优先关系)两个元组tr和ts是非支配关系,如果存在属性Ak(1 ≤k≤m),使得tr[Ai]≤ts[Ai](1 ≤i 定义4(隐藏Web数据库Skyline)隐藏Web数据库D中所有非支配关系的元组构成数据库D的Skyline,有时也称为Web数据库D的轮廓。 定义5(支配一致性约束(dominate consistence constraint))Top-k查询结果中的k个元组{t1,t2,…,tk}是Web服务器端依据Web接口查询条件获得结果元组中受支配最少的k个元组,并依据指定排名函数的元组优先关系“<”排序得到的结果,即ti(1 ≤i 平行坐标系的基本思想是将n维数据属性空间通过n条等距离的平行轴映射到二维平面上,每一条轴线代表一个属性维,轴线上的取值范围为从对应属性的最小值到最大值,这样数据库的每一个元组(或记录)可以依据其属性取值而用一条跨越n条平行轴的折线表示(这里要求对空值属性和分类属性进行适当处理和映射)。如表1的元组在平行坐标系的表示如图1所示。 Table 1 Tuples of D表1 D的元组 定义6(相交关系和非相交关系)两个元组ti和tj(1 ≤i,j≤n)如果存在属性Ak和Ar(1 ≤k,r≤m,k≠r)使得ti[Ak] Fig.1 Tuple-line diagram of parallel coordinates图1 平行坐标系的元组折线图 定义7(完全相交关系)对于任一k个元组,如果其中任何一个元组ti(1 ≤i≤k)和其他k-1 个元组存在相交关系,则这k个元组是完全相交关系。 引理1平行坐标系中任何一个元组支配其上面所有与其非相交的元组。 证明既然任一元组t0和位于其上的元组ti(1 ≤i≤n)都是非相交关系,由定义6 知t0和ti(1 ≤i≤n)均满足t0[Ak]≤ti[Ak](1 ≤k≤m),再由定义2 可知,t0支配ti(1 ≤i≤n)。 □ 引理2相交关系的元组是非支配关系。 证明若元组ti和tj是相交关系,由定义6 知存在属 性Ak和Ar(1 ≤k,r≤m,k≠r) 使 得ti[Ak] 定理1一个数据库的Skyline中所有元组都是完全相交关系。 证明(反证法)假设在数据库的Skyline中存在两个元组ti和tj(1 ≤i 定理2在数据库的Skyline中新增一个元组t,该元组将Skyline划分成两部分,和t相交的元组S1,和t不相交元组S2,那么,若t位于S2 下面,则Skyline 由S1和t构成;否则,t必位于S2上面且Skyline保持不变。 证明因为t和S1中的元组均相交,由引理2知,t和S1是非支配关系。此时,若t位于S2下面,由引理1 知,t支配S2,由定义4 可知Skyline 必由S1 和t构成。相反地,若t并不位于S2 下面,假设t出现在S2的中间,那么S2 将被t分成互不相交的两部分,这和S2 是Skyline 的一部分,由定理1知S2内的元组是完全相交的已知条件相矛盾,故t只可能出现在S2的上方,再由引理1知,S2的所有元组均支配t,最后由定义4知t不是Skyline的组成部分,故Skyline保持不变。□ 假设:查询qi的top-k结果集T满足支配一致性约束,结果集T的首条元组为t。 q0:SELECT*FROMD; 依据查询q0返回结果T,当|T|≥K时,将T的首条元组t递归定义如下查询分解q1,q2,…,qm-1;当|T| q1:WHEREA1 q2:WHEREA1≥t[A1]&A2 q3:WHEREA1≥t[A1]&A2≥t[A2]&A3 …… qi:WHEREA1≥t[A1]&A2≥t[A2]&…&Ai-1≥t[Ai-1]&Ai …… qm:WHEREA1≥t[A1]&A2≥t[A2]&…&Am-1≥t[Am-1]&Am B_Const(t):表示父节点t的分支查询条件,由根节点到该父亲节点的路径条件的合取组成。如果父节点是根节点,则B_Const(t)=TRUE。 P_Const(qi)=B_Const(t)&A1≥t[A1]&A2≥t[A2]&…&Ai-1≥t[Ai-1]:表示查询qi查询的前置条件; 上述查询可进一步简化为: q1:WHEREP_Const(q1)&A1 q2:WHEREP_Const(q2)&A2 …… qi:WHEREP_Const(qi)&Ai …… qm:WHEREP_Const(qm-1)&Am 例1假设数据库D的属性集和元组集如表1 所示,图2所示为基于top-3的相交元组查询分解树,该查询树的所有中间节点都将返回top-3结果的首条元组,相交元组查询分解的查询结果是S={t2,t4,t1,t3,t6,t5,t7},从图2 中可以看出S中的所有元组在平行坐标系中的折线是完全相交关系。 Fig.2 Intersectant tuples query decomposition tree of example 1 based on top-3图2 例1基于top-3的相交元组查询分解树 由上述相交元组查询分解树的构造可知其具有如下性质: (1)相交元组查询分解条件在属性A1,A2,…,Ai-1,Ai,…,Am-1范围上是互斥和全覆盖的。 (2)(相交关系查全性)父节点的首条元组在条件范围P_Const(qi)下,通过q1,q2,…,qm的m个查询分解找到的在属性A1,A2,…,Ai-1,Ai,…,Am上与其有相交关系的最优先元组,分解到最后将找到所有与父节点具有相交关系的元组。 (3)(同一条枝条的完全相交关系)同一条分支上的所有节点元组都具有完全相交关系。 (4)(不同枝条的非完全相交关系)由于查询条件P_Const(qi)的限制,不同分支上的节点元组可能存在支配关系,即非相交关系或非完全相交关系。 (5)(同层分解的非重复性)由于查询条件的互斥性,任何节点的查询分解都不会出现重复元组。 定理3(查全性)如果一个元组t∈D是数据库D的Skyline 中的一个元组,即t∈Skyline,则在相交元组查询分解树中存在一个查询节点qi,使得该节点的查询结果T包含元组t(t∈T)。 证明由于t∈Skyline,由定理1 得知,至少存在属性Ai,Aj(1 t[Ai]>t′[Ai]&t[Aj] 由定义8得知:在相交元组查询分解过程中将存在一个查询节点t″(t″∈Skyline) 和一个正整数k(1 t[A1]≥t″[A1]&t[A2]≥t″[A2]&…&t[Ak-1]≥t″[Ak-1]&t[Ak] 即,元组t被包含在节点t″的一个分支节点的查询结果T中,|T|≥k时,作为首条元组出现。 □ 4.2.1 基本查询分解方法 依据相交元组查询分解树的定义和Skyline元组的完全相交性质,提出如下基本查询分解方法。 基本查询分解方法的基本思路[19-20]: (1)通过深度优先或广度优先方式建立相交元组查询分解树,获得隐藏Web数据库D中所有具有相交关系的元组集S1和S2,其中S1是查询分解树的中间节点的首条元组集合,S2是查询分解树的叶子节点的元组集合。 (2)对于S1⋃S2中的元组,依据Skyline元组的完全相交性质生成隐藏Web数据库D的Skyline元组集。 4.2.2 启发式查询分解方法 为减少查询代价(远程查询次数)提高查询效率,提出如下启发式查询分解方法。 启发式查询分解方法的基本思路: (1)在基本查询分解中,每次查询分解首先在父节点的返回结果集中进行本地查询,如果查询结果非空,则不发出远程查询请求;如果查询结果为空,则发出远程查询请求。 (2)如果查询结果的首条元组t被当前查询树的某一节点的查询结果中的元组t′支配,则将t置换为t′继续分解。 定理4启发式分解方法具有查全性。 证明对于启发式的情况(1),若子节点对父节点的分解结果的本地查询非空,结果集的首记录记为t1,那么容易知道该子节点若进行远程访问所获查询结果亦非空,结果集的首记录记为t2,由隐藏Web数据库的支配一致性约束知,t1=t2,故可用非空的本地查询代替远程查询(为确保约束成立,只需保证父节点分解结果中元组出现的先后顺序在本地查询的结果中维持不变)。 对于启发式的情况(2),将t置换为t′,由于t被t′支配,那么由t′产生的分解树将更为简短,因为根据分解树的生成条件表达式,t′产生的条件表达式中必有一子项比t的上界更低,进而可以更多更快地过滤非Skyline元组,但所剩元组(包括中间节点和叶子节点)所构成的分解树中包含的Skyline 是不变的。由(1)、(2)知启发式方法的查全性。 □ 在求解服务端隐藏Web数据库的Skyline元组时查询代价的主要因素决定于远程查询次数,依据相交元组查询分解树的定义得知,远程查询次数等于相交元组查询分解树中的远程查询分支数。 定理5启发式查询分解方法的查询代价C(远程查询次数)在K≤m条件下满足如下不等式: m+1 ≤C<(|S|+[n/k])×m(k≤n) 证明从查询的分解过程得知:从最初通过Q0=SELECR*FROM D →T0查询得到的T0的首条元组t1(t1∈Skyline 元组)开始,对t1的每一次分解查询Qi,首先依据父节点的查询结果T0执行本地查询,查询的结果为Ti: 当Ti≠∅时取T中的首条元组继续m次分解; 当Ti=∅时执行远程查询; 当远程查询结果|Ti| 当远程查询结果|Ti|≥K时,再依据Ti的首条元组t1进行m次的查询分解。 由于在查询分解过程中,查询Qi的首条元组有可能被当前S1⋃S2中的元组支配,因此在查询分解树中会存在Skyline 元组被重复分解的情况,但是由于查询分解条件的属性范围是互斥的,因此Skyline元组重复分解的次数一定不会大于[n/k]次。 因此查询分解树的中间节点数不会超过|S|+[n/k],查询树中总的分支数(每一条分支代表一次查询)将不会超过(|S|+[n/k])×m。 查询分解树中,远程查询的次数必然小于查询树中总的分支数,即远程查询代价C<(|S|+[n/k])×m。 又因为D中至少有一条Skyline 元组,所以远程查询代价C≥m+1。 □ 通过模拟实验和在线真实实验两个步骤进行。在模拟实验部分采用两个数据库:学生成绩模拟数据库和实际项目中真实的房地产户型数据库,并开发了基于top-k的查询接口。由于数据库已经装载在本地,数据库的结构特性(实体的属性类型、数量和关系等)和数值特性(记录元组个数等)都是已知的,因此可以通过对这些特性值的调节来检验算法的查全性,测试它们的查询代价,以及观测它们随不同因素影响的变化趋势等。在线实验依据房谱网(http://www.house-book.com.cn)真实网站对算法进行测试。 学生成绩数据库包括10 门课程(包括5 门数值属性的考试课和5 门分类属性的考查课)且存储有100 000条记录。考试课的成绩取值范围为[0,100],考查课的成绩取值范围为(5-优,4-良,3-中,2-及格,1-差)。房地产户型数据库中设置10个属性,包含5 300余万条记录。实验中选取5个数值属性和5个分类属性。 首先,需要验证基本分解算法和启发式分解算法的查全性。在对模拟数据验证成功后,对实际的网络数据集进行抓取并全部存储在本地,然后运用本地Skyline求解算法获取正确的Skyline集,并用此对基本分解算法和启发式分解算法获得的结果集进行验证。结果表明,无论在模拟数据还是实际网络数据集上,上述两种算法均满足查全性,查全性验证完毕。此处出于完整性,进行必要的说明,不过鉴于查全性不是本文研究的重点,因此相关的实验内容就不再列出。 然后,比较基本分解算法和启发式分解算法的查询代价,也即远程查询的次数C。根据查询代价的理论分析结果m+1 ≤C<(|S|+[n/k])×m(k≤n),考察参数集{m,|S|,n,k}的变化对上述两种算法的查询代价C的影响。此处,为了便于比较两种算法,当考察一个参数影响时,固定了其他3个参数;考虑到普遍性,其他3个参数设定应当令数据集具有代表性。为此,通过分析设定了相关影响因子,以此生成各典型的数据集。主要的因子包括:Skyline 集占全数据集的比例因子,通过它可以生成稠密集、普通集、稀疏集;范围型字段和枚举型字段的比例因子,通过它可以生成不同构成的数据集;规模因子,通过它可生成规模不等的数据集。由于待比较的参数较多,相应组合的情形更多,鉴于篇幅,下面仅列出在各类典型设定中4个参数对两算法影响的代表情形,即包括属性的影响效果如图3,Skyline元组数|S|的影响效果如图4,数据集规模的影响效果如图5 和top-k中k的影响效果如图6。 Fig.3 Effect of number of attributes m on query cost图3 属性个数m对查询代价的影响 Fig.4 Effect of number of Skyline tuples|S|on query cost图4 Skyline元组数|S|对查询代价的影响 Fig.5 Effect of data set size n on query cost图5 数据集规模n对查询代价的影响 Fig.6 Effect of top-k on query cost图6 top-k对查询代价的影响 最后,实验结果表明无论在哪种情况下,启发式分解算法的代价都要优于传统的基本分解算法。 通过Web 接口来获取服务端“隐藏”的数据库Skyline 已成为Web 数据挖掘领域的一个研究热点,文中通过引入平行坐标系技术分析了数据库多维数据的Skyline 元组相交性质,在定义相交元组查询分解树和证明查全性的基础上,提出了隐藏Web 数据库的Skyline 元组的基本求解算法和启发式求解方法,并通过理论分析和实验验证了方法的有效性。 尽管如此,启发式算法的实验中,特别针对各类典型的模拟数据集的实验中,发现无效的查询在不同特性数据集中差距巨大,因而在数据集采样的基础上分析其特性,进而针对不同类型的数据集设定不同策略,达到进一步减少远程查询次数的目的。 此外,在Web 信息集成中,如何通过上述方法来有效地解决基于用户偏好的top-k查询和推荐等问题是下一步要研究的内容。3.2 基于平行坐标系的Skyline元组性质
4 隐藏Web数据库Skyline查询方法
4.1 相交元组查询树的构造及性质
4.2 Web数据库Skyline查询方法
4.3 查询方法代价分析
5 实验分析
5.1 数据集
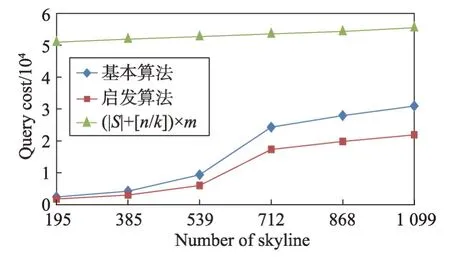
5.2 实验结果分析

6 结束语

