电热多物理耦合模拟的软件设计模式研究*

龚 平，郑宇腾，张爱清

北京应用物理与计算数学研究所，北京 100083

1 引言

电热多物理场耦合数值模拟是大规模集成电路设计的重要手段。特别是随着设计及制造工艺朝着三维系统级封装、异质异构集成的方向演进，导致功率密度显著增加，热与应力可靠性问题更加突出[1]，并且与电磁问题相互耦合、相互影响，成为影响与制约电路性能与可靠性的核心因素，因此电、磁、热、力等多物理场耦合分析是大规模集成电路设计的一个关键环节[1-4]。而大规模集成电路结构精细，工况多样，物理机理复杂，涉及电-热、电-热-力等各种不同的多物理场耦合，以及静态、瞬态、时谐等多种分析类型[2-4]。面向这种多样化的多物理场耦合分析需求，如何快速研制批量电热多物理场耦合模拟软件，是一个挑战性的问题。

基于算子分裂方法，复用单一物理场求解代码，实现多物理场耦合计算，是快速开发多物理耦合软件的有效途径。但以往国内外科研学者通常专注于物理模型和数值算法的研究，不关注代码复用，一般会将物理建模细节，甚至工程建模细节，硬编码在数值求解子程序中，导致几乎没有代码重用的可能性，耦合软件都只能从头开发。例如Jin等人[5]对直流馈电网络的电压降及热问题的研究，Shao等人[6]对高功率集成电路的电-热耦合仿真的研究，是众多从头开发电热多物理场耦合模拟软件的两个普通例子。因此为满足多样化的多物理场耦合模拟需求，需要一种高效率、高可复用、能够快速组装计算流程的多物理耦合软件开发模式，实现单一物理场求解代码一次开发，多次利用。

针对电热多物理场耦合模拟需求，本文提出了支持快速组装、高可定制的并行模拟软件设计模式。该模式的主要思路是基于可复用的电场和磁场方程模板，开发可复用的方程求解构件库，然后应用基于方程求解构件组装耦合计算流程，从而达到快速研发多物理场耦合计算软件的目的。

2 电热耦合理论方法

芯片工作时，电磁场损耗产生焦耳热，焦耳热作为温度场的热源，导致芯片温度上升；而温度升高则又会改变芯片电学参数，进而影响电磁场分布。因此在芯片的数值模拟中，至少需要考虑电场和温度场间的耦合效应[9]，涉及的电磁数值求解包括静电问题和时谐电磁问题，分别对应电流连续性方程、矢量电场波动方程，热数值模拟为稳态热平衡，对应的方程为稳态热平衡方程，物理场数据耦合需要考虑电磁场产生的热源引起的温度场变化，同时根据温度场的分布来更新电学参数。

2.1 电场和温度场方程模板

由电流连续性方程可以导出静电问题所要求解的方程[10]：

其中，σ(r)为材料电导率；U(r)为电位；Ub(r)为第一类边界上的电压值。对于电位未知量，使用结点有限元单元离散。

对于时谐电磁场，可由频域麦克斯韦方程导出矢量电场波动方程。

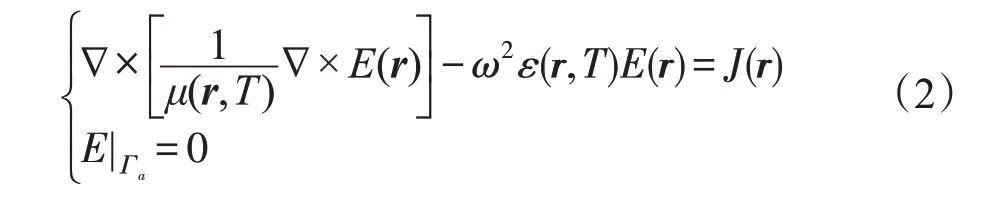
其中，μ(r)为材料磁导率；ε(r)为材料介电常数；ω为角频率；E(r)为电场；J(r)为电流源分布。对于电场未知量，使用棱边有限元单元离散。

稳态热平衡方程是：

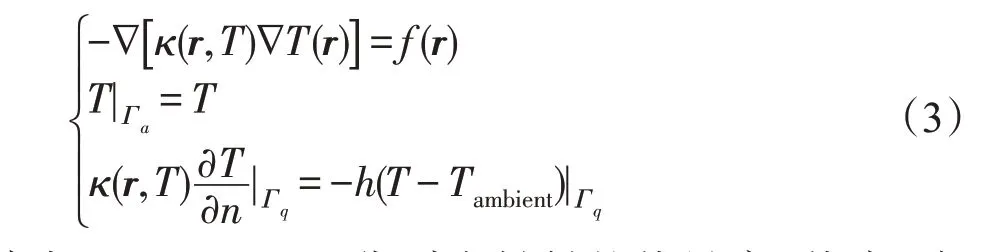
其中，κ(r,T)、c、ρ分别为材料的热导率、热容、密度；T(r)为温度分布；T为第一类边界上的温度值；h为第三类边界上的热对流系数；Tambient为环境温度；f(r)为热源项。对于温度场未知量，使用结点有限元单元离散。

在电场、电位、温度场未知量离散后，使用伽辽金方法建立有限元矩阵方程[11-12]，并通过基于Krylov子空间的迭代方法[13]求解，最终得到场分布。

2.2 电-热耦合模型

电-热耦合分析涉及正向和反向两种耦合模式，分别是电磁场产生热源的正向耦合模式和温度场改变电学参数的反向耦合[14]。

对于正向耦合，包括静电场产生的热源，计算公式为：

f(T,t)=σ|∇U(t)|2

以及时谐电磁场产生的热源，计算公式为：

f(T,ω)=σ|E(ω)|2

对于反向耦合，温度将改变电学参数。上述方程（1）、（2）中的电学参数将演变为温度和空间的函数，其形式如下：

σ(r)=σ(T(r),r)

μ(r)=μ(T(r),r)

ε(r)=ε(T(r),r)

本文的耦合处理方案是松耦合求解。每次耦合迭代中，依次求解电磁场方程，计算电磁场产生的热源，求解热平衡方程，根据温度场更新电学参数。通过温度场分布计算残差，判断是否终止迭代。

3 数理方程构件化设计模式

电热耦合模拟软件的快速组装要求仿真组件满足可复用、可互操作、可定制三个特性。可复用指的是，不修改物理过程计算构件就可以直接在计算流程中调用；可互操作指的是，物理场数据在不同物理过程计算构件间的正确传递；可定制指的是，不修改物理过程计算构件，软件开发者可以修改仿真模拟的流程和耦合过程。

而根据第2章所展示电-热场的控制方程与物理场的数据耦合，单物理场求解是多物理场耦合分析的共性，对应的模拟个性则是根据计算流程定制的数据耦合处理方法。因此，使用统一数据结构的并行编程框架，开发共性的单物理场计算构件及个性定制的物理场间耦合器，便可快速开发高效的耦合软件。

3.1 可复用：封装单物理场

基于统一的数据结构封装共性，即将单物理求解流程封装为求解单控制方程的计算构件（简称方程构件），在仿真模拟软件开发过程中实现复用。

如图1所示，封装后的方程构件具有以下功能：

（1）配置控制参数及求解操作；

（2）读取计算必须的统一数据结构的物理场数据（输入）；

（3）提供统一数据结构的物理场数据（输出）。

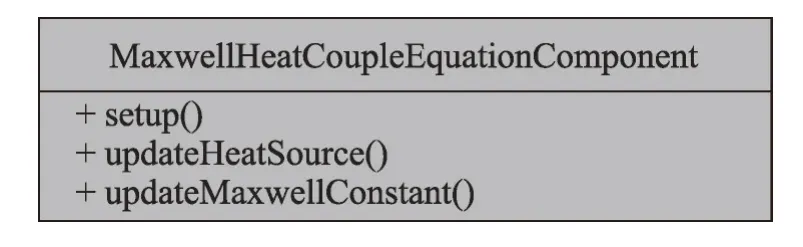
Fig.1 Coupling components in electric-thermal coupling simulation图1 电-热耦合模拟中的耦合构件

对于本文求解的电磁-热耦合问题，封装的方程构件分别是电流连续性方程构件、矢量电场方程构件、稳态热平衡方程构件，方程构件的功能和输入输出如表1所示。

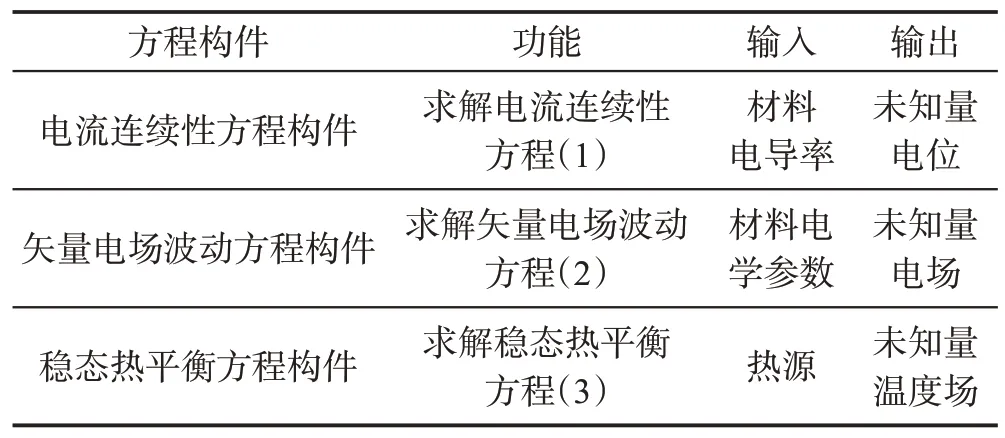
Table 1 Equation component表1 方程构件

3.2 可互操作：物理场间数据交互

在电-热耦合模拟过程中，电磁场在导体或介质中损耗，产生焦耳热，焦耳热改变温度场；温度场的改变又导致材料的电学参数发生变化。电磁场对温度场的作用通过改变焦耳热实现，温度场对电磁场的作用通过改变电学参数实现，因此焦耳热和电学参数被称为耦合变量；对于仅存在于一个物理过程中的变量（如电位）称为非耦合变量。物理场间的数据交互指的就是耦合变量的交互。

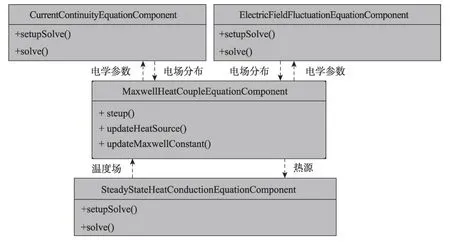
Fig.2 Equation component in electro-thermal coupling simulation图2 电-热耦合模拟中的方程构件

对于非耦合变量，由于其不需要在物理场间交互，便由所在方程构件单独管理；相对照的，耦合变量会被多个物理过程计算模块访问和修改，因此需要使用统一的数据耦合构件创建和管理，在其他的方程构件中需通过数据耦合构件，创建耦合变量和访问耦合变量。

3.3 可定制：选择方程构件和耦合构件、搭建计算流程

在3.1 节中抽象和封装单物理场控制方程的共性，形成可复用的方程构件，而对于仿真模拟中的个性部分，包括耦合变量的创建与管理部分，则会被封装成数据耦合构件；根据特定计算场景或模型分析的需求，通过组合方程构件与数据耦合构件，定制计算流程。

在电-热耦合模拟中，物理场数据耦合部分包括计算焦耳热、更新材料的电学参数，如图1。对于不同的仿真模拟应用，可以通过定制数据耦合构件，满足不同的耦合需求。

以矩形导体棒中的电-热耦合问题为例，涉及的控制方程有电流连续性方程与稳态热平衡方程，如图2 所示。电流连续性方程构件从数据耦合构件中读取电学参量作为输入，计算电场分布，并作为输出量传递给数值耦合构件；稳态热平衡方程，方程构件从数据耦合构件中读取热源作为输入，计算温度场分布，并作为输出量传递给数值耦合构件。

最终个性化软件定制时，如图3 所示，只需要在主控函数中组合使用方程构件与数据耦合构件。首先调用电磁方程构件求解电流连续性方程或矢量电场方程；然后调用物理场数据耦合构件更新焦耳热，稳态热平衡方程构件求解温度场；物理场数据耦合构件更新电学参数，最后判断计算是否结束，如果未结束开始下一轮循环。

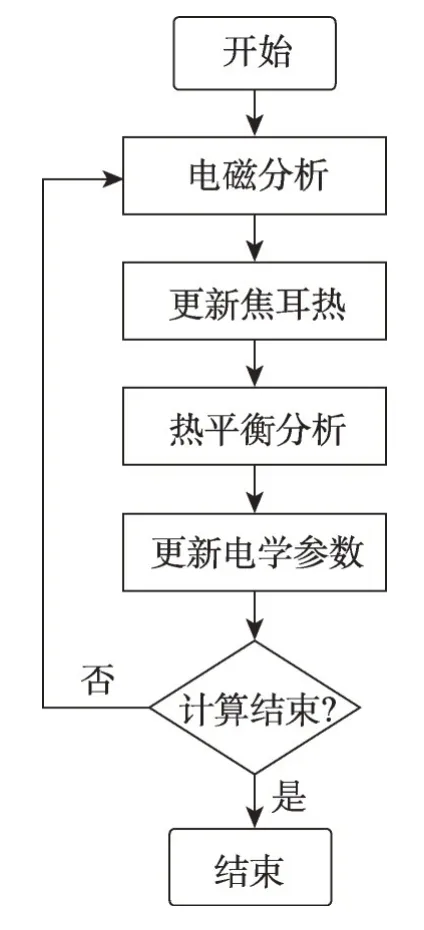
Fig.3 Computation flow图3 计算流程

4 基于JAUMIN的并行实现

并行自适应非结构网格应用支撑软件框架（J parallel adaptive unstructured mesh applications infra-structure，JAUMIN），提供超大规模并行计算和网格自适应加密等功能[15]。

本章将介绍基于JAUMIN 框架如何实现电热耦合并行仿真模拟的快速开发。

4.1 方程构件

根据JAUMIN 框架对软件结构的要求，物理过程计算构件包括网格片层次结构时间积分算法、网格层时间积分算法、网格片计算策略类。在网格层时间积分算法、网格片计算策略类中配置单个物理场的参数和计算，通过网格片层次结构时间积分算法调用网格层时间积分算法、网格片计算策略类，实现自动并行。

以矢量电场波动方程构件为例，图4为方程构件的基本结构。矢量电场波动方程构件包括的功能有读取电学参数，并计算电场E。

4.2 耦合变量的管理

在JAUMIN 框架中，使用变量管理器统一管理物理场数据，通过变量ID索引和访问。因此方程构件的数据输入输出可以通过传递变量ID实现分享数据的目的。

耦合变量的创建和管理由数据耦合构件负责，电流连续性方程构件、矢量电场方程构件和稳态热平衡方程构件通过接口可获得目标数据变量ID。方程构件与耦合构件间交互数据变量的伪代码如下所示。

4.3 定制耦合构件与组合实现计算流程

依照JAUMIN 框架要求，耦合构件接口和结构设计如图5所示。与方程构件相同，耦合构件包括网格片层次结构时间积分算法、网格层时间积分算法、网格片计算策略类，主要的功能接口包括获取耦合变量ID、计算焦耳热和更新电学参数。

计算流程定制在main函数通过组合方程构件和耦合构件实现，以静电-热稳态耦合分析为例，main函数伪代码形式如下所示。

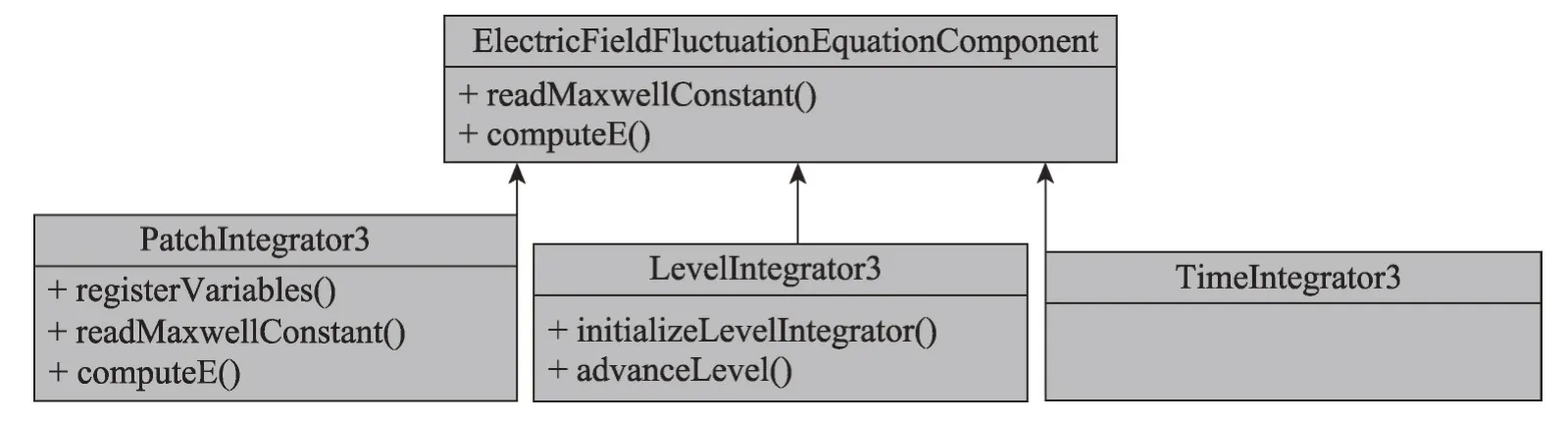
Fig.4 Equation component structure图4 方程构件结构

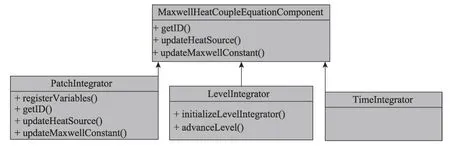
Fig.5 Data coupling component structure图5 数据耦合构件结构

5 实验验证

根据本文提出的快速组装的并行电热耦合模拟软件设计模式，编写静电分析、频域分析以及热稳态分析模块，在计算流程中根据需要组合使用电-热模块和可定制的耦合模块搭建计算流程，就可以快速完成多物理耦合模拟软件开发。

为验证本文提出的软件模式可靠性、复用性，对于电-热耦合问题，开发了以下两款软件。

5.1 静电-热稳态模拟软件

仿真程序的流程图如图6 所示。验证模型为矩形截面的导体棒，模型尺寸长、宽、高为50 mm、25 mm、10 mm，材料为铜，波导两端设为恒温边界，温度为295 K。

在仿真计算过程中调用静电分析以及热稳态分析，与原有的程序温度场分布对比如图7，其中图7（a）是定制程序仿真结果，图7（b）是原有程序仿真结果。从图中可以看出，温度场数值是一致的，定制程序的仿真结果正确。

5.2 频域-热稳态模拟软件

验证模型为滤波器[16]，如图8 所示，内部材料包括空气、硅和铜，问题的求解频率为30 GHz，目标整体尺寸长、宽、高分别为6.88 mm、4.12 mm、1.37 mm，滤波器上下表面与空气的对流系数为30 W/(m2·K)。

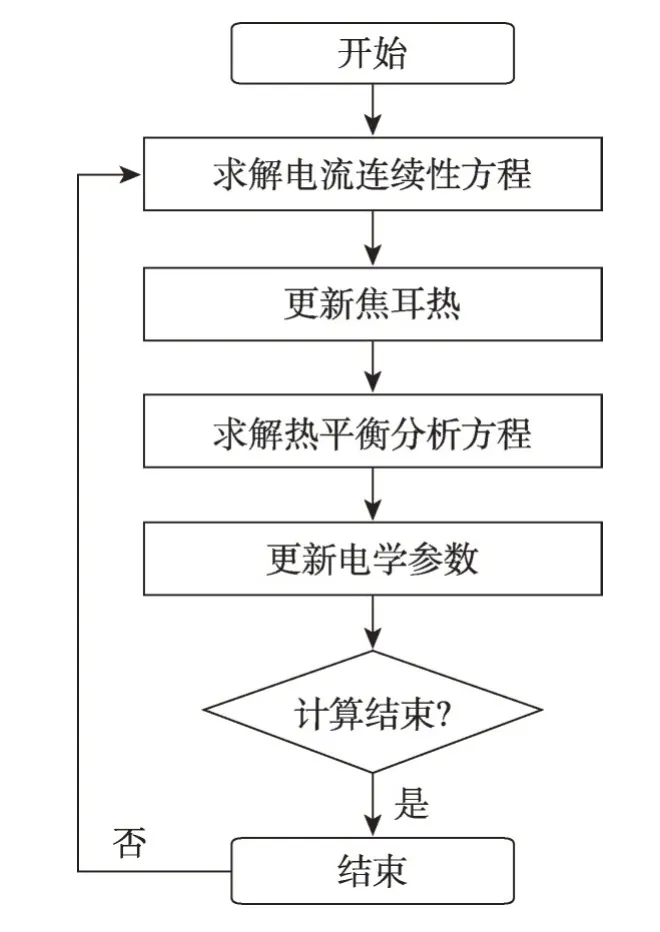
Fig.6 Flow graph for electrostatic and steady-state thermal coupling analysis图6 静电-热稳态耦合分析流程图

仿真程序的流程图如图9所示。

在仿真计算过程中调用频域分析以及热稳态分析，与原有的程序温度场分布对比如图10，其中图10（a）是定制程序仿真结果，图10（b）是原有程序仿真结果，从图中可以看出温度场数值是一致的，定制程序的仿真结果正确。

5.3 可复用的快速组装验证

本文通过对比代码复用率[17]，也就是程序中可复用软件模块与不可复用软件模块代码行数，证实了本文提出的软件设计模式实现代码的快速复用。

可复用软件模块包括上文介绍的电流连续性方程构件、矢量电场方程构件、稳态热平衡方程构件，以及数值离散模块、材料管理器。静电-热稳态分析程序、频域-热稳态分析程序中，各模块的代码行数（去掉空行和注释后）如表2、表3所示。

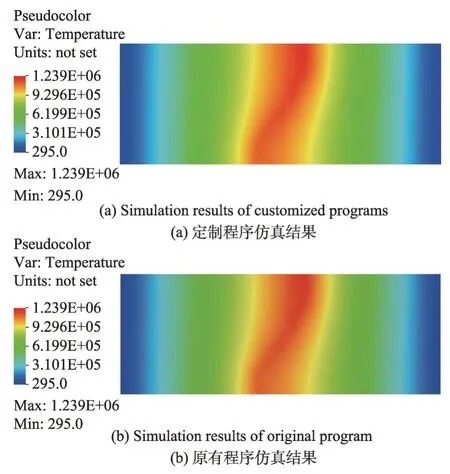
Fig.7 Example of electrostatic,steady-state thermal coupling analysis and comparison of temperature distribution图7 静电-热稳态耦合分析算例及温度场分布对比

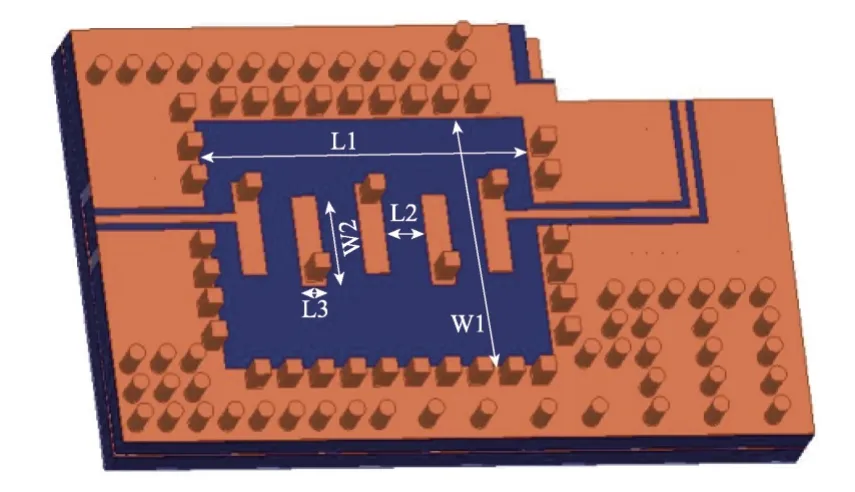
Fig.8 Frequency-domain,steady-state thermal coupling analysis model structure图8 频域-热稳态耦合分析仿真模型结构

静电-热稳态分析程序中，全部程序代码行数为7 219，可复用代码行数占全部代码行数为87.6%；频域-热稳态分析程序中，全部程序代码行数为7 888，可复用代码行数占全部代码行数为88.7%。

两个程序中，数值离散模块的代码行数最多，复用率最高，其次是矢量电场波动方程构件（表中Electric-FieldFluctuation 构件），复用率最低的是稳态热平衡方程构件（表中SteadyStateHeatConduction 构件）；不可复用代码占全部代码比例不足15%，预计后续的其他仿真模拟应用开发的工作量将会有效减少。

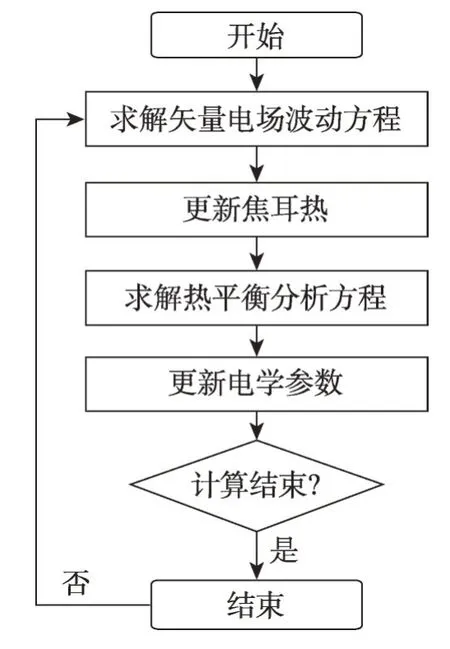
Fig.9 Flow graph for frequency-domain and steady-state thermal coupling analysis图9 频域-热稳态耦合分析流程图

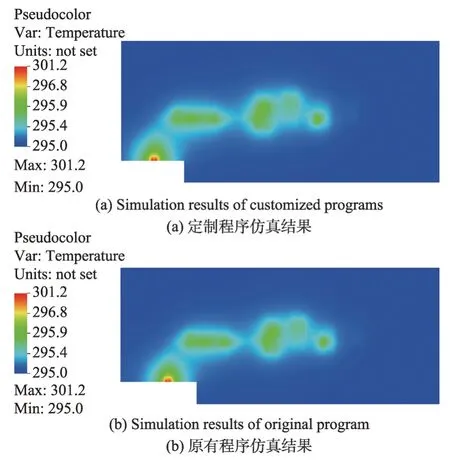
Fig.10 Example of frequency-domain,steady-state thermal coupling analysis and comparison of temperature distribution图10 频域-热稳态耦合分析算例及温度场分布对比

6 结束语

本文研究多物理仿真模拟中，电-热耦合模块的快速组装。实验结果证明该方法在保证计算结果正确的基础上，实现了电子芯片仿真模拟中的电-热耦合模拟的快速组装开发。本文提出的软件复用模式是否适用于更多更复杂的非线性多物理耦合或多尺度多物理耦合应用，还有待进一步研究和验证。

Table 2 Number of code lines of coupled electrostatic,steady-state thermal analysis software表2 静电-热稳态耦合模拟软件代码行数

Table 3 Number of code lines of coupled frequency-domain,steady-state thermal analysis software表3 频域-热稳态耦合模拟软件代码行数