可信第三方的伪名签名方案研究*

陈 虹，陈红霖，黄 洁，肖成龙，郭鹏飞，金海波

辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105

1 引言

随着移动网络不断普及并深入人们的生活，越来越多的人开始注重个人的信息安全，寻求更加可靠的网络访问方式。为了保护用户信息的安全性和匿名性，经过研究者们的长期摸索，逐渐提出了一系列可行方案。

1982 年Chaum[1]第一次提出了盲签名的概念。在盲签名模式下，签名者不能获取签名请求者所请求签名的内容。由于上述特性，使其迅速在数字现金、电子投票等匿名环境中得到广泛应用。但盲签名完全的盲性使签名者失去了对签名内容的控制力。1996 年Abe 等人[2]提出了部分盲签名的概念。该方案允许签名请求者在签名中嵌入与签名者预先协商的、且不能被移除或非法修改的公共信息。例如签名的时间、签名的有效期等。部分盲签名方案为签名的隐私性和可控性找到了新的平衡点，在某些需要保护隐私，但又强调安全性的场景中有着广阔的应用前景。

对部分盲签名的研究已延续了20 多年，在2005年和2013 年，Chow 和Tang 等人[3-4]分别对部分盲签名进行了阐述。2016 年，Liu 等人[5]对基于身份的无可信私钥生成中心的部分盲签名方案进行了改进，解决了其对篡改公共信息攻击安全性不足的问题。2018 年，Ye 等人[6]提出了基于格的部分盲签名，该方案能够有效抵抗未来量子算法的攻击。学术界目前研究的主要方向集中在基于身份的部分盲签名方案上，但是根据Li等人[7]在2012年所述，无证书部分盲签名同样具有巨大的发展前景。

如今，移动网络已经成为日常生活中的一部分，并为人们的生活带来了许多的便利。但是正如浏览器中加入“不追踪”选项的意图，现在的网络访问将用户的个人信息完全暴露在大众的视野之中，公众的个人信息正面临巨大的危机。1990年，Chaum[8]提出了零知识证明的又一途径，无条件不可链接伪名。该方案将用户的个人数据变更为非个人数据，以确保数据不会涉及到某个可识别的具体的人。该方案自提出以来，被广泛应用于车辆路线规划、公共分享等需要用户数据，但也需要保护用户隐私的参与式活动的研究中，国内外专家学者也对其进行了深入研究[9-16]。

2012 年，Bender 等人[17]在德国的个人身份证上对基于域的伪名签名进行了初步尝试，但签名设备可能被认证机构所控制，认证机构可以伪造用户的签名。2013年和2014年，Bringer[18-19]分别提出了防共谋的域伪名签名，以及一个为动态域伪名签名建立的安全模型，确保域伪名在域内是可被链接的，但在域外不可链接。2018年，Kutyłowski等人[20]在Bringer的基础上进行改进，确保了发布者无法伪造用户伪名，加强了获取用户真实身份所需要的权限，保证了即使中央认证机构和域管理机构合谋，也只能链接用户的伪名，而无法获取用户的真实身份，但其获取用户真实身份的过程仍可能存在伪造或重放攻击的风险。

针对Kutyłowski方案存在的问题，本文在其基础上进行了改进，提出了基于可信第三方的双重伪名签名方案，保证了即使认证机构和域管理机构合谋也不能对用户的伪名进行链接，提高了伪名签名方案的安全性。同时，相较于大多数以大量增加运算量为代价的第三方方案，本文方案在一次完整过程中的总时间增加了大约30 ms。但在实际操作中，方案的主要过程，伪名签名和验证过程，所消耗的时间与原始方案基本相同。此外，通过可信第三方的追踪机构获取用户的真实身份，不仅可以识别错误的或被篡改的用户真实身份信息，而且在效率方面具有极大的提升。

2 相关理论

2.1 群

设G是一个非空集合，“∙”是它的一个二元运算，如果满足封闭性、结合律、单位元存在、逆元存在，则称G对∙构成一个群。特别地，当∙写作乘法时，G为乘群；当∙写作加法时，G为加群。

群G的元素个数叫作群G的阶，记为|G|。当|G|为有限数时，G叫作有限群，否则G叫作无限群。如果群G中的二元运算还满足交换律，那么G叫作一个交换群或阿贝尔群。

如果S是群G的子集，则S所生成的子群是包含所有S的元素G的最小子群。等价地说，是可以用S的元素和它们的逆元中的有限多个元素的乘积表达的G的所有元素的子群。如果G=，则称S生成G,S中元素叫作生成元或群生成元。

2.2 离散对数问题

在整数中，离散对数是一种基于同余运算和原根的对数运算。而在实数中对数的定义logba是指对于给定的a和b，有一个数x，使得bx=a。相同地，在任何群G中可为所有整数k定义一个幂数为bk，而离散对数logba是指使得bk=a的整数k。在该问题中，已知x和b求解a是容易的，但已知b和a求解x是困难的。

2.3 决策性Diffie-Hellman问题（DDH问题）

假设一个阶为q的（乘法）循环群G，生成元为g。DDH 假设是指对于统一随机选取的a，b∈Zq，给定ga、gb、gab“看起来像是”群G中的随机元素。这个直观的概念可以描述为以下两个概率分布在计算上是不可分的：

（1）（ga，gb，gab），其中a、b从群Zq中随机独立选择。

（2）（ga，gb，gc），其中a、b、c从群Zq中随机独立选择。

第一个元组被称为DDH元组。

3 Kutyłowski的方案

首先简要介绍Kutyłowski的方案[20]如下：

3.1 系统建立

假定一个素数阶q的群G，G具有DDH 困难问题，且设g为G选定的生成元。Zq表示阶为q的整数群。

认证机构（certification authority，CA）持有随机选择私钥SKICC，SKM，SKL∈Zq和对应的公钥PKICC，PKM，PKL，其中

为了去掉伪名，CA 持有随机选择的私钥δ、γ和对应的公钥Δ、Γ，其中Δ=gδ和Γ=gγ。

3.2 用户的预密钥

CA为签名设备预置了满足式（1）的私钥(x0′，x1′，x2′)和成对的、同样满足上述线性方程的(x0″，x1″，x2″)，其中IDA是用户A的身份令牌，详见3.3节。CA还为签名设备准备了与上述私钥对应的公钥(P0′，P1′，P2′)和(P0″,P1″,P2″)，其 中随机选择x1′∈Zq（同样选择不同的x1″)、x0′、x2′（同样计算不同的x0″、x2″）是基于上述线性方程得出的。

向用户提供包含(x0′，x1′，x2′)，(x0″，x1″，x2″)的签名设备。同时，直接为用户提供公共密钥。

3.3 创建IDA

在注册用户A时，CA 独立地随机选择s∈Zq，令IDA=s，将包含的明文记录存储在CA 的数据库DBID中（IDA值未发布，直接销毁）。

3.4 签名密钥私有化

用户对预密钥进行私有化处理，确保即使CA保留了预密钥，也无法伪造用户签名私钥。

3.5 域的参数

其中，指数d1由CA随机选择，指数d2由目标域管理机构随机选择。

3.6 创建签名

（1）随机选择k0、k1、k2。

（3）计算签名者基于域的伪名：

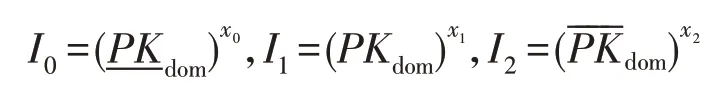
（4）计算随机元素k0、k1、k2的参数：

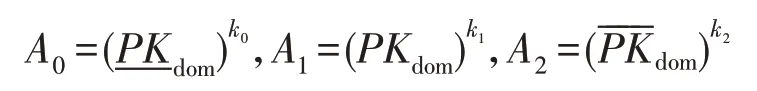
（5）对于要签名的消息m，计算c=Hash(Q,I0,A0,I1,A1,PKdom,I2,A2,Hash(m))。

（6）计算Schnorr签名的第二个参数：s0=k0-c×x0modq,s1=k1-c×x1modq,s2=k2-c×x2modq。

（7）输出签名(c,s0,s1,s2)以及伪名I0、I1、I2和相关域的标识。

3.7 验证签名

3.8 获取用户真实身份

（1）域管理机构（掌握d2）计算：

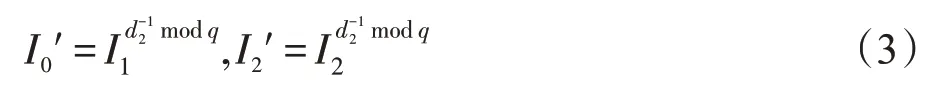
（2）CA（掌握d1）计算：

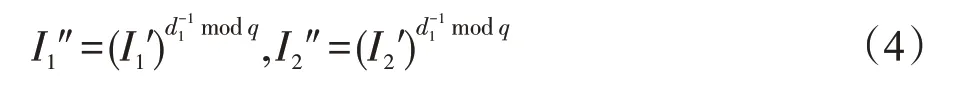
I1″应该等于应该等于

（3）CA计算I=(I1″)γ×I2″，应该等于

（4）CA 在DBID中查找条目I，找到具有不当行为的用户A。

4 本文方案

Kutyłowski方案存在下面主要的安全问题：

（1）如果CA 与域机构合谋，则可以链接用户的不同伪名。

（2）在获取用户真实身份时，域机构可能对CA存在误报，甚至是欺骗。

针对上述安全问题，本文提出了基于可信第三方的双重伪名签名方案，不仅解决了上述问题，而且在获取用户真实身份的响应速度上具有较大的提高。本文方案使用部分盲签名向CA申请伪名许可证书，通过此许可证书向域认证机构（domain certificate authority）申请伪名并在域内进行签名和业务访问。在必要的时候可由可信第三方的追踪中心（认为是系统中不可被攻破的）对用户伪名执行去匿名化。

本文方案的总体交互图如图1所示。

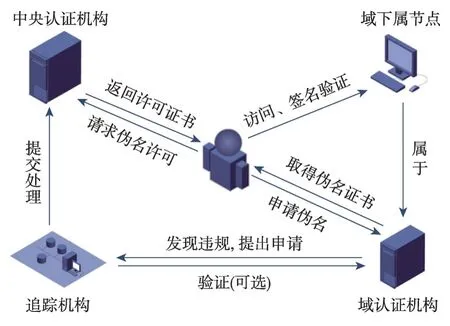
Fig.1 Scheme interaction diagram图1 方案交互图

4.1 系统建立

假定一个素数阶q的群G，G具有DDH 困难问题。设g为G的生成元。

CA持有的密钥：

（1）身份IDCA；

（2）随机选择私钥SKICC，SKM，SKL∈Zq；

（3）相应的公钥PKICC、PKM、PKL，其中

为了去掉伪名，域管理机构和TA共享以下密钥：

（1）随机选择的私钥δ、γ；

（2）域管理机构独立计算Δ=gδ。

域管理机构持有的密钥：

（1）身份IDdom；

（2）私钥SKdom；

TA持有的密钥：

（1）身份IDTA；

（2）随机选择的私钥SKTA∈Zq；

用户持有的密钥：

（1）身份IDUser；

（2）随机选择的私钥SKUser∈Zq；

4.2 用户的签名密钥

域管理机构为用户准备了如下用于签名的密钥：

私钥(x0′,x1′,x2′)满足：

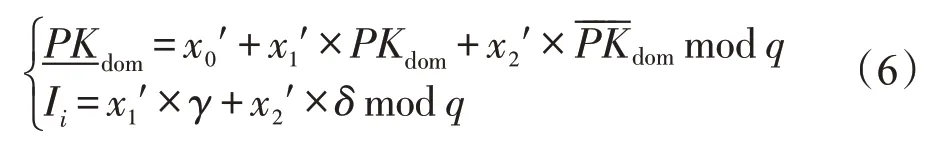
同样满足线性方程组（6）的成对私钥(x0″,x1″,x2″)。

与上述私钥对应的公钥(P0′,P1′,P2′)和(P0″,P1″,P2″)，其 中

随机选择x1′∈Zq（同样选择x1″）、x0′、x2′（同样计算x0″、x2″）是基于上述线性方程得出的。Ii是用户申请的伪名，详见4.3节。

用户在得到上述密钥之后，随机选取r，计算R=1-rmodq。进而得到签名密钥(x0，x1，x2)=r×(x0′,x1′,x2′)+R×（x0″,x1″,x2″)modq。同理可根据Pi=(Pi′)r×(Pi″)R，i=0，1，2 计算公钥(P0，P1，P2)。

4.3 获取伪名

本文方案将伪名的获取分为了两个阶段，分别是用户向CA 申请伪名许可阶段和用户向域管理机构申请伪名阶段。

4.3.1 申请伪名许可

（1）用户发送身份IDUser，申请的伪名数n，当前时间t以及用户使用私钥SKUser对上述参数的签名和公钥PKUser给CA，同时记录时间t。||表示连接操作。

（2）CA 在收到消息后，首先查看用户身份IDUser是否在黑名单中，若是则拒绝此次伪名申请，否则使用公钥PKUser验证签名若验证成功，则同意用户IDUser的注册，返回允许。

（3）对第i个伪名，用户随机选取数αi、βi，计算ai=(αi×βi)modq并将ai和i发送给CA，0 ≤i≤n。

（4）CA验证用户是否注册，若是则取当前时间ti，定义伪名的有效期exp，并计算ai×Qi，其中Qi=IDUser||ti||IDCA||exp，同时使用私钥SKICC对ai×Qi进行签名。最后发送给用户。若用户未注册返回步骤（1）。

（5）用户收到消息后首先去除盲因子αi，得到，然后使用CA 的公钥PKICC验证签名的合法性，判断IDUser||ti||IDCA||exp的真实性。若签名存在问题，则从步骤（1）重新开始。CA 每次发送的时间ti应是不同的，如果用户检测到ti的顺序发生错误或在规定时间内某时刻签名丢失，则从步骤（2）重新开始。同时，将ti与初始时间t进行比较，可以防止不诚实的CA 使用以前的消息进行重放。若验证成功，用户和CA分别计算公共信息info=αi×βi×(IDUser||IDCA||exp)。然后，用户计算伪名

（6）得到伪名后，用户向CA 申请伪名Ii的部分盲签名，公共信息为info，CA比对双方的info是否一致，若不一致则从步骤（1）重新开始，若一致则接受对伪名Ii的申请，并向用户返回签名结果。用户对得到的签名进行去盲，得到允许使用伪名Ii的许可证书PPC(info,Ii)。

4.3.2 申请伪名证书

（1）用户向域管理机构发送PPC(info,Ii)、info、Ii、域管理机构在收到信息后首先从Ii中分离出βi×Qi，并验证签名是否正确，若正确则验证PPC(info,Ii)是否正确。仅当两次验证均正确时，才能够证明CA允许用户使用伪名Ii。此时域管理机构并不知道此用户的真实身份。

（2）验证成功后，域管理机构向用户返回伪名Ii的证书：

（3）用户收到伪名证书后验证其是否有效，若无效，则重新申请伪名；若有效，则可以在签名中使用此伪名。

4.3.3 用户伪名存储

域管理机构在发布用户的伪名Ii时，计算并将存储在自身数据库中。

4.4 创建签名

假设使用伪名Ii的用户持有密钥(x0,x1,x2)，在公钥为的域，对消息m进行签名。签名过程与文献[11]中的过程类似：

（1）随机选择k0、k1、k2。

（3）计算用户对于域的参数：

（4）计算用户对应于域的伪名：

（5）计算对随机元素k0、k1、k2的参数：

（6）对于要签名的消息m，计算c=Hash(Q,D0,A0,D1,A1,D2,A2,Hash(m))。

（7）计算Schnorr 签名的第二个参数s0=k0-c×x0modq，s1=k1-c×x1modq，s2=k2-c×x2modq。

（8）输出签名(c,s0,s1,s2)以及域伪名D0、D1、D2和用户对于域的参数

4.5 签名验证

4.6 获取用户真实身份

如果具有身份IDdom的域管理机构发现具有违规行为的用户，则执行下述步骤：

（1）TA 直接执行D=(D1)γ×D2，结果应为并将所得条目发送给域管理机构。

（2）域管理机构在收到TA 发来的D之后，在自身数据库中查找相关条目，并返回与之对应的Ii。

（3）TA在收到域管理机构发来的伪名Ii之后，可选择使用此伪名与该域公钥PKdom计算以进行验证。若验证成功则继续执行，此过程为可选。

（4）TA从伪名Ii中分离出βi×Qi和使用自己的私钥SKTA解得到βi，进而解出Qi，得到其中的IDUser。

（5）TA将得到的IDUser发送给CA，由CA对用户IDUser进行相应的处理。

在该过程中，CA、域管理机构和TA 之间可以采用任何合适的身份验证方法。

5 方案分析

传统数字签名的提出是为了保证信息的完整性和真实性，以及用户对签名消息的不可抵赖性，即消息是正确的，不能被他人伪造，且消息签名者也不能否认自己的签名。伪名方案除了保证上述安全性之外，还可以更好地保护用户的隐匿性。本文的方案中，只有可信第三方能够获取用户的真实身份，其他任何一方或者多方合谋也无法获取用户真实身份，甚至是将不同的伪名进行链接，具有较高的安全性。

5.1 正确性

本文方案假设追踪机构TA 是不会妥协的权威机构，如政府。对于伪名TA 不需要其他任何机构的帮助就可以确定用户的真实身份。TA 首先分离出再使用自身私钥SKTA解出βi就可以得到Qi，进而得出用户的真实身份IDUser。

对于伪名D0、D1、D2：

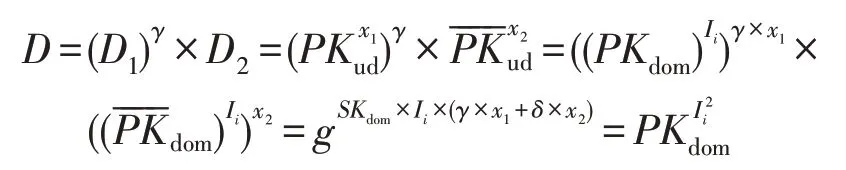
对于伪名签名，证明过程与文献[11]类似：

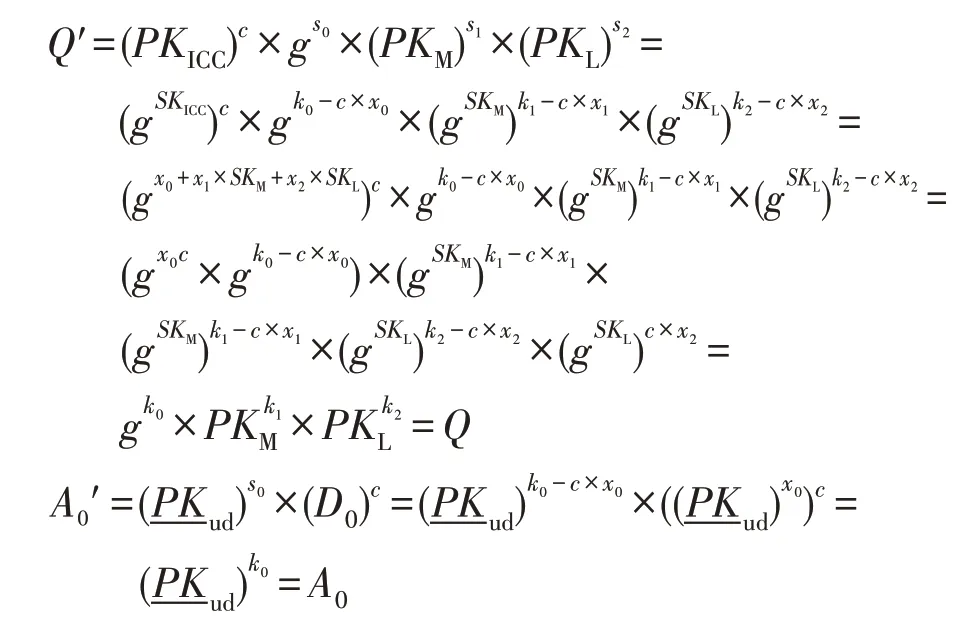
使用同样的方法可以验证A1′、A2′。

5.2 安全性

（1）匿名性：在伪名申请阶段，用户首先与CA进行交互。CA与用户共享用户的真实身份IDUser，部分盲签名的公共信息info=αi×βi×(IDUser||IDCA||exp)。同时，CA还知道ai=(αi×βi)modq。但是，αi、βi由用户独立、随机地选择，故CA不能从中分离出βi，进而获取用户的真实身份。

用户在得到使用伪名Ii的许可后，与域管理机构共享了伪名域管理机构同样知道info=αi×βi×(IDUser||IDCA||exp)，但域管理机构既没有掌握ai=(αi×βi)modq，也没有掌握TA 的私钥SKTA，故不能从共享信息或伪名中得到用户的真实身份IDUser。

由于CA 和域管理机构分别掌握了用户的真实身份IDUser和伪名Ii，故两者均不能将其真实身份和伪名进行链接，因此在伪名申请阶段伪名Ii和用户真实身份IDUser是不可链接的，也就成功保证了用户的匿名性。

在伪名签名阶段，用户使用具有匿名性的伪名Ii构建自身基于域的身份，由于只有TA和域管理机构具有解开域伪名所需的私钥δ，故只有两者能够解出进而得到Ii。

因此本文方案能够保证用户的匿名性。

（2）不可伪造性和不可抵赖性：在伪名申请阶段，如果CA 做出妥协，将用户的身份IDUser替换成IDUser′，则用户可以在下一步的验证中发现。例如，CA 将发送给用户，其中Qi=IDUser||ti||IDCA||exp，若CA 将IDUser替换为IDUser′，或CA将同一用户以前的消息对此次交互进行重放，则用户在收到消息的验证中将会失败，从而拒绝此次验证。若CA 修改info中的信息也会得到相同的结果。

在伪名签名阶段，用户基于伪名Ii与域参数一起生成新的基于域的伪名D0、D1、D2，这三个伪名在域中可以相互链接，即若用户使用D0访问服务器，则该服务器同样可以知道D1、D2，以此来完成对伪名签名的验证。但对于域之外的敌手，由于缺少域参数敌手无法完成对签名的验证，更不能伪造签名。对于强大的敌手，假设其能够得到域中公开的所有信息，甚至能够得到大量的伪名签名，可以通过得到伪名Ii，即敌手能够解决DDH 困难问题，这与方案前提不符，故不成立。即使敌手获得了用户的伪名Ii，敌手也不能通过Ii=x1×γ+x2×δmodq得到x1或x2，说明敌手无法伪造用户的伪名进行签名。

相反，若不诚实的用户想要欺骗CA和域管理机构以此来逃避可能出现的后果，也是不允许的。例如，若用户在伪名申请阶段试图欺骗CA，使用非法身份IDUser′替换原始身份。首先，CA 拒绝接受用户使用IDUser′与其进行交互，故用户得不到使用IDUser′的signSKICC(ai×Qi)。而用户没有构造ti||IDCA||exp))的能力，除非用户能够伪造CA的签名。

对于域管理机构，由于此域管理机构掌握用户签名的预密钥，那么其是否可以通过私有化后的公钥得到私有化后的私钥，进而模仿用户，假设域管理机构可以做到，即域管理机构知道一个α使得xi=α×xi′+(1-α)×xi″，i=0,1,2 成立。这个问题可以化为域管理机构知道一个β使(xi-xi′)=β×(xi″-xi′)成立，这样β应该满足即 域管理机构能够解PKud的离散对数，以得到β×(x0″-x0′)，故假设不成立。

在原始方案中，若域管理机构使用错误的密钥对域伪名进行去匿名化，它可能给CA提供一个不存在的用户，某些情况下还可能指向一个真实存在的用户。在本文方案中去匿名化由TA独立执行，域管理机构仅用于存储此伪名的记录，且TA可以快速地验证域管理机构提交的伪名是否正确。因此本文方案保证了用户伪名签名的不可伪造性和不可抵赖性。

（3）不可链接性：由于目前缺乏对不可链接性的明确定义，本文引用文献[11]中对于不可链接性的定义：给定一个用户在所有域中的伪名和签名，除了参数为的域，不存在能够确定伪名D0、D1、D2是否对应于密钥(x0,x1,x2)的域。在D0、D1、D2的离散对数未知的情况下，敌手选择是或否的概率各为。在域参数未知的前提下，敌手正确选择的概率不会大于假如敌手选择了与之对应的密钥x0、x1、x2，即敌手得到了伪名Ii。但即使是域管理机构也仅仅知道与伪名Ii相关的info，而此info对于每个伪名的信息都是不同的，且缺少ai的敌手也无法从该预共享信息中得到IDUser。

因此本文方案可以有效保护用户伪名签名的不可链接性。

5.3 性能分析

本文使用i5 四代处理器，主频2.6 GHz，4 GB 内存，Win10_64位系统进行仿真。

本文方案在申请伪名阶段使用了标量乘运算，与使用指数运算相比具有更加高效的运算速率。在本文的仿真环境下，进行1 024位的指数模运算需要大约6.4 ms，进行标量乘法运算的时间可以忽略不计，使用扩展欧几里德算法计算乘法逆元大约需要1.0 ms，Hash运算的时间大约为0.01 ms，RSA（Rivest-Shamir-Adleman）签名的时间为6.5 ms，验证的时间为0.11 ms，故着重考虑方案中的指数运算和RSA 签名的时间。在本节中使用P 表示指数模运算，用I 表示求逆运算，用S 表示RSA 签名。方案理论上的时间对比如表1 所示。理论上本文方案与原始方案耗时的对比如图2所示。仿真实验的结果如表2所示。

由于每次仿真时运行时间存在波动，故表2 中的数据为运行10 次求取平均值后的结果。在总时间上，本文方案比原始方案多出了近20 ms，增长量为原始方案的8.7%。但在CA 的运算时间上本文方案仅为原始方案的40%，提升了相同条件下CA 可以同时提供的服务数量。在域管理机构和用户的运算时间上分别有一定程度的增长。同时，本文方案获取用户真实身份仅需要6.3 ms，仅为原始方案的24.2%，可以有效降低因用户违规而带来的潜在损失风险。

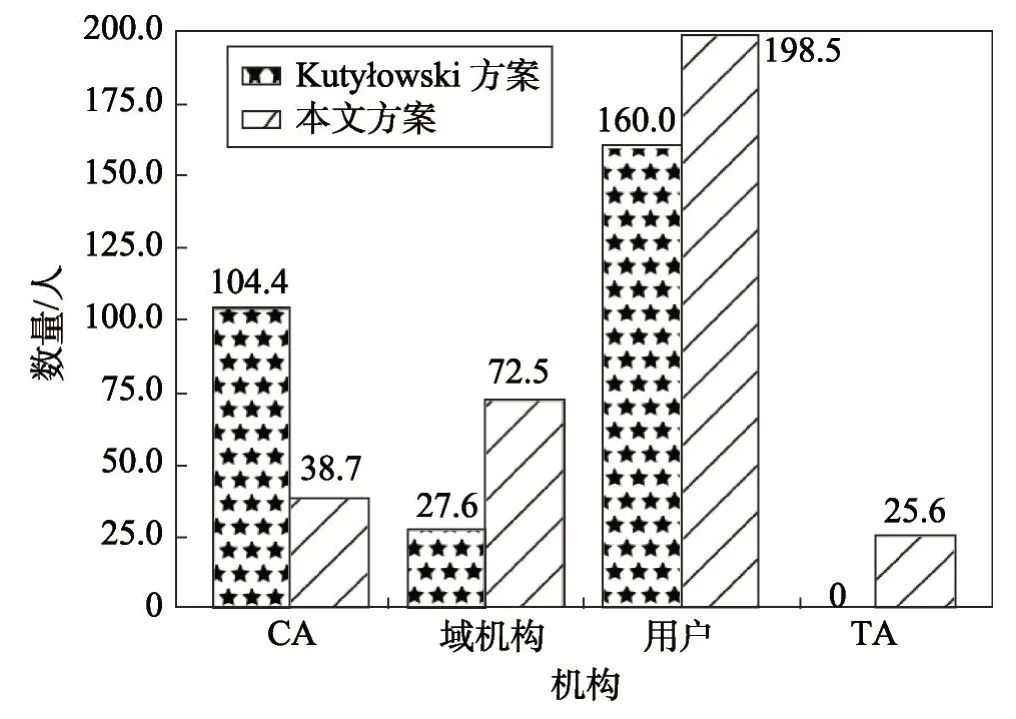
Fig.2 Time-consuming comparison diagram图2 方案耗时对比图

由图2 可知，本文方案大幅度降低了CA 的运算时间，但也增加了域管理机构和用户的计算时间。在本文方案中，CA 将与系统中的所有用户进行交互，降低CA 的耗时，也就提高了整个系统的门限。由于CA 在授予用户伪名许可之后就不再与用户或者域管理机构进行交互，故用户和域管理机构耗时的增加并不会给CA的运行带来影响，域管理机构和用户运算时间的增长也在可接受范围内。CA 耗时的降低意味着系统可以同时服务的用户数量增长了1倍。TA是本文方案对于具有违规操作的用户进行快速响应的保证。从表2可知，在获取用户的真实身份时，本文方案仅需要6.3 ms，在原始方案的基础上缩减了近2/3。

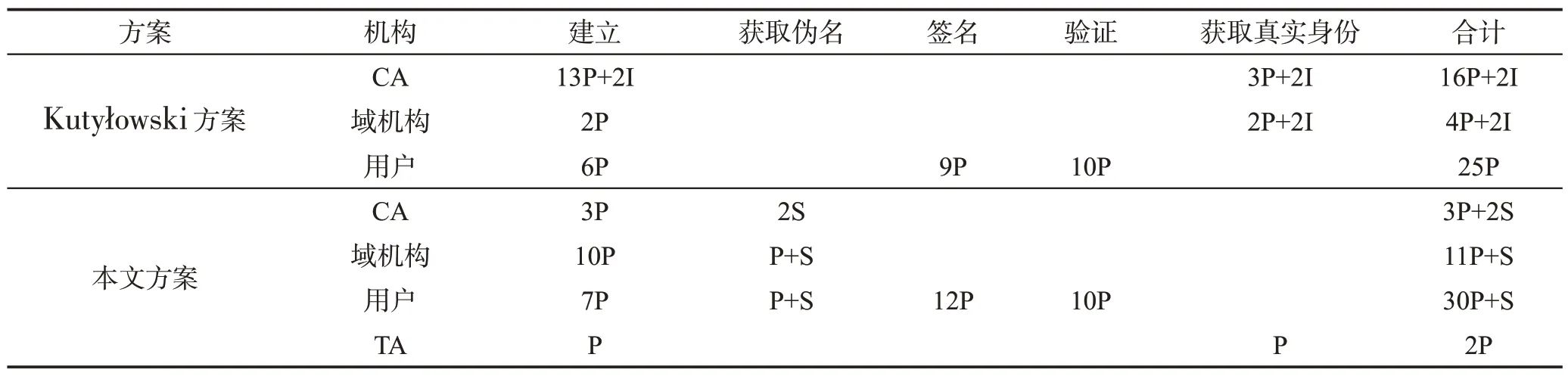
Table 1 Time comparison of scheme in theory表1 方案理论时间对比

Table 2 Comparisons of simulation results表2 仿真结果对比

在实际操作中，用户会一次性向CA请求大量伪名许可证书以满足其在未来一段时间（可能一个月）内的伪名需求，用户向域管理机构发出的伪名申请可能与用户申请伪名许可证书的时间存在一段时间的差距，故CA和域管理机构之间的运算是完全独立的，这更说明了本文方案在降低CA消耗上有比预期更好的表现。

与原始方案相比，本文方案效率提高的同时安全性也略有提高，在保证签名的完整性、真实性（不伪造）、不可抵赖和隐匿性的同时，解决了原始方案中可能存在对同一用户的不同伪名进行链接的问题，在开放的互联网时代更好地保护用户的隐私，也保证了用户信息的安全性。

6 结束语

在网络时代，人们更加强调隐私性和安全性，这两者似乎是无法同时完成的，但伪名系统的出现解决了这个问题。本文介绍了一种使用伪名进行签名的方案，在此基础上提出了一种基于可信第三方的双重伪名签名方案。用户首先从CA 获取大量的伪名许可证书，然后在之后的访问中使用某个许可证书向目标域机构获取伪名，并使用该伪名在域内进行新的伪名签名和验证。通过对比两个方案的各项属性和仿真实验，发现本文方案将原始方案中CA的计算时间降低到40%，提高了系统的门限。同时使用一个第三方的可靠机构进行用户真实身份的追踪，此方案在追踪用户真实身份上具有巨大的优势，且可以防止域管理机构的欺骗。但是本文方案也给用户带来了更多的负担，使得方案仅适用于对安全性要求较高，要求对违规用户快速反应，且具有一定运算能力的场景，例如个人网上银行。

本文还有一些没有解决的问题，例如是否能够构建一个完全不依赖于其他机构的TA 以绝对地掌握追踪用户真实身份的权力，以及能否在第一阶段的伪名获取中使用某个困难问题构造伪名以满足更高的安全性要求。或者如何解决用户在一次性获取大量伪名的情况下，对用户的伪名进行撤销。尽管可以简单地通过让TA 来维护方案中存储用户信息的数据库来解决第一个问题，但这必将给TA带来巨大的成本负担，使得TA 也有成为系统门限的可能。将沿着这个方向继续研究。