声子BTE应用的并行和优化研究*

文敏华，刘永志，鲍 华，胡 跃，沈泳星，韦建文，林新华+

1.上海交通大学 高性能计算中心，上海 200240

2.上海交通大学 密西根学院，上海 200240

1 引言

DGX-2是NVIDIA家族最强大的人工智能系统，基于NVSwitch技术，整合16块完全互联的TeslaV100GPU构建的可扩展框架。整个系统显存达到512 GB，共计拥有40 960个双精度CUDA（compute unified device architecture）核心。除了多块GPU卡带来的强大计算能力，DGX-2中采用的NVSwitch技术提供了GPU之间的高速互联，NVSwitch 拥有18 个51.5 GB/s 的NVLink 端口。基于其强大的计算能力以及GPU 间的高速通信网络，DGX-2 在通用计算领域也拥有着巨大潜力。

声子玻尔兹曼输运方程（Boltzmann transport equa-tion，BTE）能够在亚连续尺度下模拟平衡或非平衡态的热传导现象，并且由于在大范围长尺度上的有效性持续受到欢迎[1]。在最近四十年中，半导体技术快速发展不仅使得芯片计算能力大大加强，也使得功耗越来越高；当前热问题正成为决定芯片性能、可靠性和成本的主要因素。因此通过声子BTE方程模拟计算半导体器件的热传导对了解其基本物理机制和发展散热策略具有重要意义。但是当前最为成熟的有限体积法求解声子BTE方程来模拟工程实际问题时，仍然存在计算量大、计算时间长的困难。

基于将DGX-2强大的计算能力以及高速的通信速率应用于声子BTE 方程求解的初衷，本文做了如下工作：（1）使用CUDA框架对采用有限体积法的声子BTE求解器的迭代部分进行了针对GPU移植与并行优化。在GPU 上实现了迭代计算的主要步骤，如声子散射项的计算、线性方程组的求解、晶格温度平衡态分布的计算等。（2）采用3 种方式，MPI+CUDA，NCCL（NVIDIA collective communications library）函数以及CUDA-AwareMPI，实现了对声子BTE方程的多GPU的并行求解。总而言之，本文有以下两点贡献：

使用CUDA框架首次在GPU上实现了声子BTE求解的迭代过程，并在单块V100 上，较Intel Xeon Gold 6248单核性能提高了5.3倍至31.5倍。

在DGX-2 平台上实现了对声子BTE 的多GPU并行求解，测试了3 种并行方式对程序性能的影响，其中性能最优的NCCL 库函数版本在8 台DGX-2 共128块V100上实现了83%的强扩展并行效率。

2 相关工作

有限体积法等确定性方法求解声子玻尔兹曼输运方程较为困难。因为只有对角度做到足够数量的离散才能够满足网格无关性的验证，而这就使得该方法会产生数量庞大的离散方程，对计算量的需求较为庞大。针对这种情况，Ali 等[2]提出了求解声子BTE的几种大规模并行计算的策略和算法：（1）基于声子模式；（2）基于角方向；（3）混合声子模式和网格单元的并行方式。对三维器件类硅结构进行非平衡态的瞬态模拟，将计算域离散为604 054 个网格单元，使用400 个角度对角方向进行离散，40 个声子模式对声子散射曲线进行离散，使用400个进程计算一个时间步长都需要1 h。Ni等[3]也对有限体积法求解声子BTE 方程进行了并行计算研究，提出了基于空间域和声子模式的并行策略。其中空间域较为适用全反射性的声子BTE模型，能够较好地扩展到128核并行。以上都是对声子BTE 进行CPU 并行求解，可以看出并行的核数为数百核左右，并行规模并不大。

关于使用GPU 进行科学计算方面，在电动力学领域，Priimak[4]在GPU 上实现了描述半导体超晶格中电子传输的基于有限差分法的玻尔兹曼输运方程，在GTX 680上相较于CPU串行版本获得了118倍的加速。在流体力学领域，Calore等[5]在GPU上实现并优化了可求解大规模湍流的格子玻尔兹曼方法，在K80 上，相较Xeon-Phi 获得了4 倍加速比，并且最多扩展到32个GPU并行计算，并行效率约90%，总的性能接近20 Tflops。在科学计算领域，Bell 等[6]基于不同稀疏矩阵存储格式实现其相应的矩阵向量乘，并在结构化网格和非结构化网格上进行测试，相较于4 核CPU 并行，GPU 计算达到了10 倍以上的加速比。Anzt 等[7]研究了预处理的BiCGSTAB（biconjugate gradient stabilized method）、CGS（conjugate gradient squared method）和QMR（quasi-minimal residual）等Krylov求解器在GPU上的效果，证明了在性能方面，相比于ILU预处理器，Jacobi预处理通常会有更高的效率。

从以上工作看出，GPU 在通用计算领域应用较广，但是目前还没有在GPU 上对有限体积法求解声子BTE方程进行相关研究。本文不仅尝试在GPU上对该方程进行求解，且使用角方向的并行策略扩展到128块GPU上进行计算，并取得83%的并行效率。

3 背景介绍

3.1 声子玻尔兹曼输运方程

声子玻尔兹曼输运方程是一个7 维非线性积分微分方程。目前求解该方程的方法基本有3种：（1）随机性方法；（2）格子玻尔兹曼方法；（3）确定性方法。随机性方法如蒙特卡罗法能有效求解这类高维偏微分方程[8]。但它最大的问题在于求解实际工程问题时需要避免结果的统计波动，但这样的代价过高[9]。格子玻尔兹曼方法仅用于在简单的二维结构中求解声子BTE方程[10-11]。同时，格子玻尔兹曼方法角度与空间离散不能相互独立，离散方式不合适会极大影响结果的准确性[12-13]。基于离散的确定性方法，如离散坐标法（discrete ordinate method，DOM）[14]、有限体积法（finite volume method，FVM）[15]和有限单元法（finite element method，FEM）[16]等广泛用于声子BTE的求解。采用离散方法产生的离散方程数目庞大，对求解的计算量需求也非常庞大。

声子是晶格振动的能量量子，其能量与频率有关。频率和波矢之间的关系为色散曲线，在计算中，连续色散曲线难以直接处理，因此采用两种简化的计算模型：灰体模型和非灰模型。灰体模型将所有声子归于一个群体；而非灰模型，将色散曲线离散成若干个声子模式。以下以非灰模型为例介绍声子玻尔兹曼输运方程。通过结合声子散射项和基于能量的声子玻尔兹曼输运方程，可得到如下所示的在弛豫时间近似下的声子能量玻尔兹曼输运方程：

3.2 基于有限体积法的声子BTE求解

采用有限体积法对声子BTE 方程进行离散，将其变成一系列可求解的低维方程。对角度、计算域及色散曲线进行离散，可得到如下形式的离散方程：

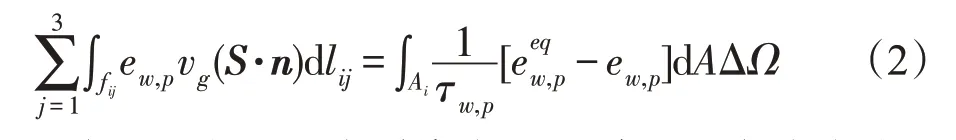
下标i和向量S分别代表空间单元和角度方向，因此对于每一个声子模式的每一个角方向及其每一个空间上的单元来说，采用一阶迎风格式，以方向s1为例，式（2）将会有一个如下形式的离散方程：

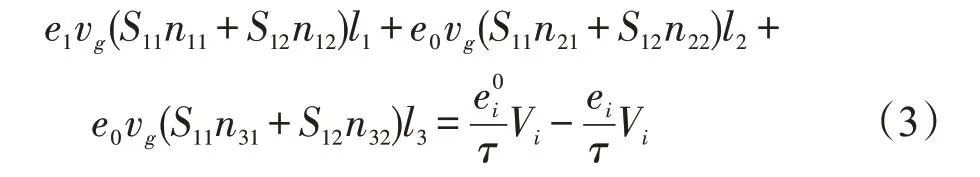
在假定当前的平衡态分布函数后，该离散方程会变成一个线性方程，而对每个角方向以及整体的区域来说，将会有如下线性方程组：

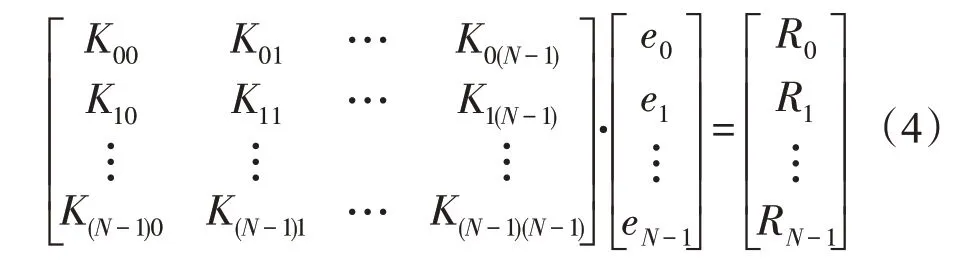
系数矩阵中Kij表示第j个单元对第i个单元的影响系数。对该线性方程的求解可得到该方向下的能量密度分布。关联角度之间及声子模式的能量密度，可以求解温度和平衡能量密度分布函数。

4 声子BTE方程在DGX-2集群的移植优化

在使用有限体积法求解声子BTE 方程中，根据对色散曲线的简化不同分为灰体与非灰模型，本文采用非灰模型来求解声子BTE方程。为求解非灰模型稳态的能量密度分布和温度分布，需要将角度间的能量密度进行关联，不仅需要考虑角度间的影响，还要考虑每个声子模式间的影响。

4.1 声子BTE方程求解过程在GPU上的实现

声子BTE方程在GPU求解流程如图1所示。算法的关键步骤如下：

（1）读入网格文件、边界条件以及参数文件，获取所有声子模式的迁移速度、比热容和弛豫时间。

（2）假定每个声子模式上所有方向的能量密度分布的值，初始化为0；计算离散后的角度控制方向。

（3）根据一阶迎风格式得到式（4）中每个声子模式及其所有角方向上的系数矩阵。

Fig.1 Process of solving non-gray phonon BTE model图1 声子BTE非灰模型求解过程

（4）进行CPU内存与GPU显存之间数据传输，主要数据为每个单元之间的影响系数。

（5）计算声子散射项，使用BiCGSTAB 算法求解线性方程组，求解每个网格单元的能量密度分布。

（6）求解新的温度分布和平衡态分布函数。

（7）计算能量密度分布新旧值之差，验证是否满足收敛条件。若满足收敛条件则停止计算，输出结果，否则继续（5）、（6）步骤。

由于整个迭代过程均在GPU 上实现，因此迭代过程所需数据一次性传入显存中，之后在GPU 上完成迭代过程中数据的更新，这样减少了GPU 与CPU间的数据传输，提高了计算效率。通过上述步骤得到稳态的能量密度的分布和温度分布，之后可以求得热流量，从而可以得到如热导率这样的宏观特性，完成对介观尺度下传热问题的模拟。

4.1.1 线程分配策略

在GPU 上实现的迭代计算部分的函数，如声子散射项函数、声子模式温度函数、晶格温度函数以及平衡态分布函数，不同网格单元间没有数据依赖。因此可使每个CUDA 线程对应一个相应的网格单元，GPU并行计算过程中，每个线程利用上一次迭代计算的结果或者是上一阶段计算函数输出的结果，完成相应网格单元中的数据的计算，进而完成整个迭代过程的计算。

4.1.2 数据存储结构

声子BTE 方程维度较高，迭代计算过程所需的数据，如能量密度值，除空间维度，还额外拥有声子模式以及角方向这两个维度。其中空间维度使用网格编号表示，因此数据一般存储在三维数组当中。由于GPU 函数是以网格单元进行的CUDA 线程分配，因此计算过程中相邻线程间访问的是数组中同一声子模式和角方向下，相邻网格单元间的数据。为了能够利用GPU合并访存特性，简化CPU、GPU端数据传输，数据采用如图2所示的一维数组进行存储。

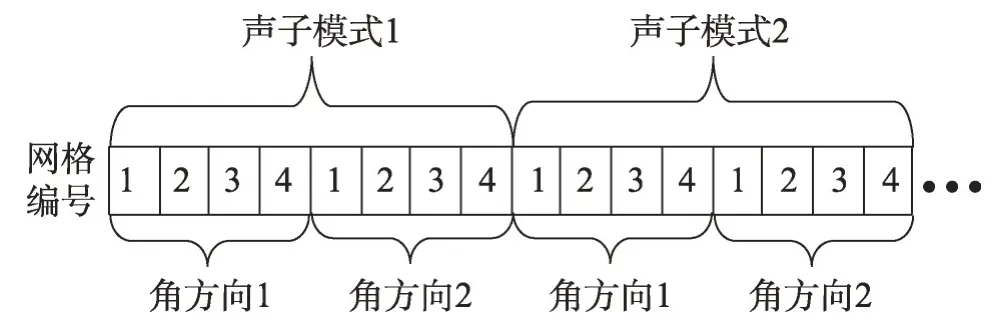
Fig.2 Data storage format图2 数据存储结构

4.2 BiCGSTAB算法实现流程

上一节描述的算法中最关键和耗时的步骤是通过求解离散后的声子BTE线性方程来确定声子能量密度分布（4.1节步骤5）。因为必须针对每个角方向和声子模式求解声子BTE 线性方程组，每一次迭代需进行大量线性方程组求解。在本研究中，使用预处理稳定双共轭梯度法（BiCGSTAB）[17]求解线性方程。该算法如下所示：

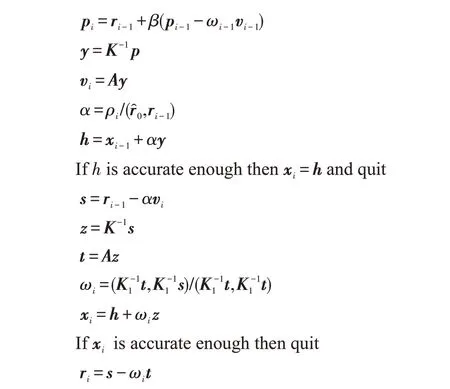
Jacobi预处理方法易于在GPU并行计算，相较于ILU 预处理方法有更好的性能[7,17]，因此本文采用Jacobi 预处理方式，该方式为最简单的预处理形式，其预处理矩阵为原矩阵的对角矩阵。

整个求解过程流程如图3所示。算法的主要部分是稀疏矩阵向量乘（sparse matrix-vector multiplication，SpMV）、点积（Dot）以及标量向量乘和向量加（alpha X plus Y，AXPY）。其中CPU 负责求解过程的流程控制，核心计算部分在GPU 中进行。上述算法在计算过程中，若出现关于r0的点积值为零，需要对x0、r0以及其他参数如ρ、α、ω等重新进行初始化并继续进行迭代计算。因此在计算过程中，需要将一些参数传输到内存，使用CPU 判断是否需要重新初始化以及计算是否收敛。

4.2.1 GPU上稀疏矩阵向量乘的实现

SpMV 在线性方程组求解算法中占有重要的地位，许多学者对其进行了研究。Bell 等[6,11]在GPU 实现了不同稀疏矩阵格式的SpMV计算，发现SpMV的性能主要受稀疏矩阵存储格式以及核函数线程分配方式的影响。

由于本文研究的应用中网格单元的系数，如3.2节式（4）所示，仅受相邻3个网格单元的影响，即每行影响系数最多为3 个，因此整个系数矩阵为稀疏矩阵。由于ELL（Ellpack）格式适用于分布较为均衡的稀疏矩阵，且SpMV 实现方式简单，因此本文采用ELL格式稀疏矩阵。

Fig.3 Implementation of BiCGSTAB on GPU图3 BiCGSTAB算法在GPU上的实现流程

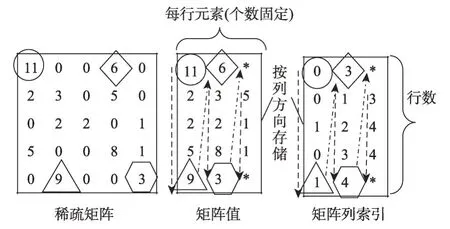
Fig.4 ELL sparse matrix storage format图4 ELL稀疏矩阵存储格式

ELL格式存储方式如图4所示，采用两个二维数组来存储一个n×k的矩阵（k为包含非零元素最多行的非零元素数目）。在实际使用中，使用两个一维向量按列方向对矩阵进行存储。使用ELL 格式的SpMV 算法在GPU 内易于并行实现，计算过程中每个CUDA 线程计算矩阵的一行，由ELL 存储方式可知，CUDA线程对矩阵值以及列索引的访问均是连续的，能够充分利用GPU合并访存特性。

4.2.2 GPU上点积计算的实现

点积计算需要进行GPU规约计算。为了规约的方便，划分块时，块内线程数为2的指数倍。该方式可使每个线程访问共享内存时不会发生bankconflict。考虑到GPU 中warp 内线程是同步的，不必进行显式线程同步。因此当活动线程均在同一warp 时，可直接进行warp 内规约计算，进而减少了线程同步的次数，提高了计算效率。

由于采用多个块（Block）进行点积计算，因此整个规约的过程分为两个阶段：第一阶段采用多个Block，首先计算出向量中每个值的乘积，之后进行块内规约计算，并将当前块内规约结果顺序存入中间数组中；第二阶段仅使用1个Block，对中间数组进行规约求和，规约方式同上，最终可求得向量点积的值。

4.2.3 GPU上AXPY实现

在GPU 上并行计算AXPY 较为简单，为向量中每个数据分配一个线程即可。同时可将前后步骤间有数据依赖且并行方式相同的函数合并到一个CUDA 内核中，这样就可避免双倍的数据加载，减少了内核数量，节约内核调用开销。例如在求解线性方程组中，会有如下所示的相邻计算。

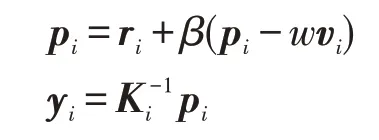
其中，K为Jacobi 预处理矩阵，实际计算过程为向量乘，并行过程与AXPY 一致，因此可以将两步操作融合成一个CUDA 函数。该方式不仅简化了代码，而且更为重要的是利用了数据的局部性，每一个线程计算的结果可直接应用到下一阶段计算中。

4.3 基于角方向的大规模并行策略

声子玻尔兹曼输运方程通常有3 种并行策略：（1）计算域分解，该方式能做到较大规模扩展，但是本文应用针对的是二维计算域，网格规模较小，若将其分解成更小的网格，则难以发挥GPU 多线程的优势；（2）基于声子模式的并行，该方式虽然较为容易实现，但是声子模式的数量一般为数十个，不能做到较大规模的并行；（3）基于角方向的并行，角方向的数量比声子模式大一个数量级，采用角方向并行能够进行数百个进程并行计算。因此为了做到较大规模的并行计算，本研究采用基于角方向的并行策略。本文使用3种不同方法实现了该并行策略，其中第一种实现方式如图5所示。

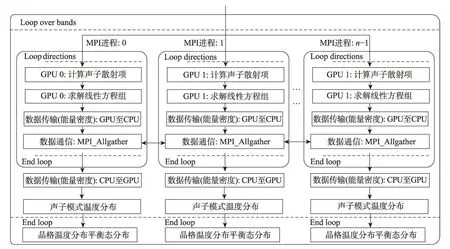
Fig.5 Parallel strategy based on angle directions图5 基于角方向的并行策略

4.3.1 MPI+CUDA

如图5 所示使用的是MPI+CUDA 的并行策略，即一个MPI 进程控制一个GPU 设备。在初始化阶段，获取MPI进程号rank，以及节点上GPU设备数量gpu_count，并将MPI进程映射到GPU设备上gpu_id=rank%gpu_count。在DGX-2 节点上，一个节点有16个V100，因此一个节点分配16 个MPI 进程，每个进程对应一个GPU设备。

求解声子BTE 方程的迭代过程中，不同角方向的声子散射所需数据为上一次迭代计算结果，与本次迭代计算无关。因此不同角方向可以并行执行。不同MPI 进程计算不同角方向，并在GPU 上完成该角方向线性方程组求解。由于在计算声子模式的温度分布中，每个网格单元需要对其所有角方向的能量密度进行求和。因此每个进程求得该角方向的能量密度后，需将结果数据从设备端传输到主机端，然后通过MPI_Allgather函数使得每个进程均可获得所有角方向的能量密度；最后将所有角方向能量密度传输到GPU中完成对声子模式温度的计算。然后继续计算其他声子模式下角方向的相关数据，最终求得当前迭代过程中的晶格温度和平衡态分布。

4.3.2 CUDA-AwareMPI

如4.3.1 小节所述的常规的MPI 实现，需首先将数据传输至CPU内存中，之后使用MPI函数；而使用CUA-AwareMPI 实现，可直接传输GPU 中的数据。从图6、图7 两种实现方式可以看出，使用CUDA-AwareMPI的实现，其代码更简洁，编程更容易。

Fig.6 Traditional MPI send and receive scheme图6 传统MPI send receive模式

Fig.7 CUDA-AwareMPI implementation图7 CUDA-AwareMPI实现方式

除此之外，使用CUDA-AwareMPI 能够使数据传输的操作都会被流水化且能够透明化地使用GPUDirect-RDMA的加速技术。该技术使得GPU中的数据可以直接被送到网卡进行传输，从而消除了GPU到CPU设备的时间消耗。这样也就显著增大了GPU和其他节点的通信效率。

使用CUDA-AwareMPI 与4.3.1 小节所述的并行方式类似，仅需进行两点改动即可，一是省略CPU和GPU 间数据通信的过程，二是将MPI 函数传输的数据改为GPU缓冲区数据。

4.3.3 NCCL函数

NCCL[18]是NVIDIA提供的GPU间的集合通信函数库，实现了all-reduce、all-gather 和reduce-scatter 等集合通信函数。可以在使用PCIe、NVLink 和NVSwitch的平台上实现高通信速率。其中2.0 版本可以进行跨节点间的GPU 通信，并可进行网络拓扑检测以及自动使用GPU DirectRDMA。为了在原并行程序的基础上使用NCCL函数，采用一个进程分配一个GPU的方式。

NCCL库的使用方式为，首先完成对MPI的初始化，之后在0 号进程上创建unique ID 并广播到其他进程，最后创建NCCL 的通信子。上述步骤完成后，即可使用NCCL中的集合通信函数。

使用NCCL 函数对声子BTE 进行并行求解，仅需在4.3.1小节所述方式上进行如下3点修改：（1）增加NCCL相关初始化函数；（2）略去CPU与GPU数据传输过程；（3）使用ncclAllGather函数进行集合通信。

5 实验结果及分析

5.1 实验环境

本研究实验所采用硬件配置如下，CPU 为Intel Xeon Gold 6248,架构为Cascade Lake，主频为2.5 GHz，核心数为20，双精度浮点性能为1.6 Tflops。节点内存大小为192 GB；GPU版本测试使用的是NVIDIA的DGX-2平台，其中该平台采用的GPU为V100，5 120个单精度CUDA核心，2 560个双精度CUDA核心，双精度浮点性能达到7.5 Tflops，显存带宽可达900 GB/s；DGX-2 内部通过NVSwtich 桥接器支持16 个全互联的V100 GPU卡。

性能测试对比采用CPU-GPU 并行计算和仅采用CPU 串行计算的加速效果。其中GPU 计算采用的CUDA 框架版本为9.2，串行CPU版本中进行线性方程求解采用的是PETSc（portable，extensible toolkit for scientific computation）[19]中函数，其中PETSc版本为3.10。对4个算例进行了GPU加速性能的测试，其中每个测试算例均为二维计算域，且计算域大小、边界条件、迁移速度和弛豫时间等参数均相同，网格及网格数量不同。算例网格数量分别为6 282、11 974、18 060及24 912。其中网格数量为24 912的算例，在实际二维问题的研究中属于规模较大的算例。串行版本中不同网格算例内存使用量分别为0.90 GB、1.85 GB、3.68GB、6.70GB，GPU显存使用量约为0.30GB、0.81GB、1.00 GB、1.24 GB。内存数据量较大主要是因为CPU计算过程中需要使用二维矩阵，并将其压缩为ELL格式稀疏矩阵，而GPU显存中仅存储压缩后的ELL稀疏矩阵。声子BTE方程求解过程中，离散声子色散曲线的声子模式个数为1，离散的角方向的个数为256。

5.2 GPU加速性能测试

图8 所示为使用单卡V100 相较于Intel Xeon Gold 6248串行版本的迭代过程的加速效果。纵坐标为单次迭代计算的时间，横坐标为不同网格大小的算例。由于本文旨在在GPU上实现BTE迭代求解过程，因此仅比较了GPU 版本与CPU 串行版本间的加速性能，未与CPU并行进行对比。

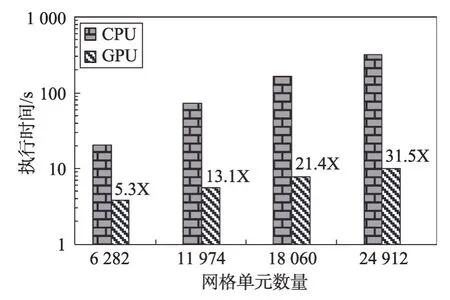
Fig.8 Speedup of GPU for different mesh counts图8 不同网格数目的GPU加速比

图8中显示的加速比针对的是迭代部分的时间，这是因为整个迭代的步数在103至104量级之间，迭代过程之外部分的耗时相对较少，对加速比的影响较小，因此仅比较迭代过程的加速比。迭代过程的CPU-GPU 混合计算需考虑数据传输的开销，本文的实现方式是在迭代计算前将GPU迭代所需数据全部传入显存中，迭代过程中的数据在GPU 显存中获取并计算更新。因此迭代过程中，GPU 仅需将与计算流程有关的系数传入内存。迭代过程中主机端与设备端数据传输为迭代时间的1.1%～1.2%。这是由于迭代过程中传输的数据多为单个参数，即单个浮点数，数据量小。

从图8 中可以看出，随着测试算例网格数量增加，GPU加速效果越来越明显。算例1中网格数量为6 282，算例4为24 912，算例4网格数量约为算例1的4 倍，其串行CPU 版本迭代时间为算例1 的15.6 倍，而其GPU 版本迭代时间仅为算例1 的2.6 倍。这是由于GPU 并行过程中，多数函数中CUDA 线程数与网格数有关，而当网格数量较小时，其使用的CUDA线程（thread）数也较少，未能充分利用GPU 的性能。同时GPU可以通过线程块的切换掩盖数据的访存延迟，因此当网格数量较大，线程块数量较多时，可以充分利用该特性，提高并行效率，因而在本例中GPU对越大规模数据进行并行加速，其效果越明显。

5.3 多GPU并行性能测试

采用4.3节基于角方向的并行策略，对多GPU并行强扩展性能进行测试。由于本文旨在实现声子BTE 程序的GPU 加速以及实现多GPU 版本的声子BTE 程序，因此多GPU 并行的加速比是以单GPU 迭代时间为基准，并未与CPU 并行进行对比。测试使用算例为上述网格大小为24 912 的算例。每个DGX-2 节点有16 块V100GPU，共有8 个节点。最多扩展到128个进程，其强扩展性能如图9所示。

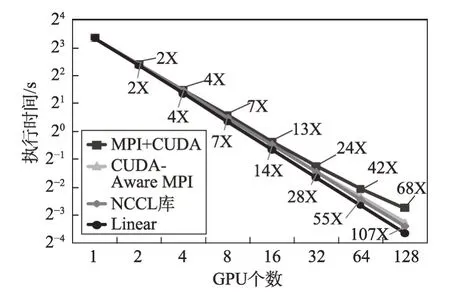
Fig.9 Strong scalability for different parallel methods图9 不同并行方式的强可扩展性

图9 中横坐标为GPU 个数，一个MPI 进程对应一个GPU设备，图中标注出了并行效率最好的NCCL库函数方式，以及并行效率最差MPI+CUDA 方式的加速比。其中使用MPI+CUDA 的版本，扩展到128卡上，相较于1 块GPU 卡，其加速比为68，其并行效率为53%；使用CUDA-AwareMPI 技术的并行版本，128卡上加速比为97，并行效率为76%；使用NVIDIA的NCCL库实现并行的版本，128卡上加速比为107，其并行效率为83%。采用NCCL 库以及CUDA-AwareMPI的方式，在同一节点可利用NVSwitch实现GPU间直接高效通信，节点间通信则利用了GPUDirect-RDMA技术。而MPI+CUDA方式，首先需要通过PCIe（peripheral component interconnect express）将GPU 中的数据传输至CPU，之后进行节点内通信以及将数据传入IB（infiniBand）网卡进行节点间通信。由于通信方式的不同，使得使用NCCL函数相比MPI+CUDA实现方式性能提升57%。由此可以看出，基于NVLink和NVSwitch 技术的GPU 间通信相比传统方式更快速和高效。

6 结束语

本文提出了采用非结构化网格的有限体积法求解声子玻尔兹曼输运方程（BTE）的GPU并行加速方法，并在8台DGX-2集群上进行了移植和并行优化。在GPU上实现了整个迭代过程，减少了主机端与设备端的数据传输，同时在求解线性方程组时，通过规约过程的循环展开以及内核融合等优化方法，在单块V100GPU上，网格单元为2.4万的算例，相较于Intel Xeon Gold 6248上的串行版本获得了31.5倍的性能提升。

同时，本文实现和评估了3 种多节点多GPU 并行的方法。采用MPI+CUDA的并行方式并行效率最低，而采用CUDA-AwareMPI以及使用NCCL函数均能充分利用NVSwitch和GPUDirectRDMA带来的通信性能增益。其中使用NCCL 库函数的并行方法最为高效，在8 台DGX-2（128 块NVIDIAV100）上获得83%的并行效率，比纯MPI版本提升达57%。

目前仅实现了基于角方向的并行策略，该方法需对网格能量密度进行集合通信，由于当前网格规模并不大，因此对性能影响较小。若对三维问题并行求解，网格规模会提升一个数量级，则其对性能的影响会较为明显。因此未来会考虑实现基于声子模式的并行，该方式通信频率较少，但是会有负载不均衡问题，因此需采取相应策略进行优化。此外本研究中仅采用Jacobi 预处理方式，虽然其较容易并行，但是收敛较差，因此接下来考虑测试不同的预处理矩阵的性能。同时将会测试更多的算例并且尝试使用不同的矩阵格式与线性方程求解器来优化单块GPU上的性能。

致谢感谢上海交通大学高性能计算中心程盛淦老师在DGX-2设备的使用上提供的帮助。