具有动态子空间的随机单维变异粒子群算法*
邓志诚,孙 辉,3+,赵 嘉,3,王 晖,3
1.南昌工程学院 信息工程学院,南昌 330099
2.江西省水信息协同感知与智能处理重点实验室,南昌 330099
3.鄱阳湖流域水工程安全与资源高效利用国家地方联合工程实验室,南昌 330099
1 引言
为解决传统优化算法无法解决的复杂优化问题,研究者们受萤火虫闪烁吸引其他萤火虫的行为启发,提出萤火虫算法(firefly algorithm,FA);受蜜蜂采蜜行为启发,提出人工蜂群算法(artificial bee colony,ABC);受鸟群觅食行为启发,提出粒子群优化算法(particle swarm optimization,PSO)。
粒子群优化算法是由Kennedy和Eberhart在1995年提出的群智能优化算法[1-2]。该算法具备计算快速和易实现等优点,作为群体智能算法的重要分支,得到了众多学者广泛深入的研究。且已应用于图像处理[3-4]、工程设计[5]、无线传感网络[6-7]、经济和模式识别等众多领域。
粒子群优化算法具有高效、实现简单等特点,已成功应用于许多现实优化任务[8],但存在多样性差、易早熟收敛等问题,制约了粒子群优化算法的发展。为克服上述问题,众多学者进行了大量研究。文献[9]通过检测粒子健康度,自适应过滤懒惰粒子,并引入引导因子过滤异常粒子。文献[10]在分析粒子群算法进化方程的基础上,通过在振荡环节采用互不相同的参数值调节算法的勘探与开发能力。文献[11]在粒子只受全局最优解影响的情况下,加入锁定因子使粒子所受影响呈规律性,并与惯性权重配合,进一步提升算法性能。文献[12]对种群粒子的运动轨迹进行分析,在标准PSO 速度更新公式上添加限制因子,确保种群收敛并提高收敛速度。文献[13]按照当前全局最优更新的次数是否达到预设门限值,将种群分为正常和早熟两种状态,当种群在正常状态,采用固定惯性权重的标准PSO公式进化;在早熟状态则引入矢量高斯学习策略,为精英粒子增加服从高斯分布的随机步长,且精英粒子进行矢量高斯学习的维度随种群的进化而减少,以增强种群多样性。文献[14]中采用列维飞行作为随机扰动步长,算法首先为种群各粒子预设一个阀值,当粒子未能自我更新的次数达到预设的阀值时,则使粒子绕当前全局最优做列维飞行,探索更多新区域;否则,按标准更新公式更新种群。
文献[15]根据种群历史最差和最好粒子的适应值,将当前每个粒子根据其适应值划分不同等级,并分配对应的理想速度以更新粒子位置。算法给每个粒子分配专属的惯性权重和加速因子,并把此三个参数作为问题的三个维度处理,将粒子当前位置到下一代位置的欧式距离绝对值定义为粒子的绝对速度,再根据粒子绝对速度和理想速度的关系更新三个参数。文献[16]将标准PSO 位置更新公式中的速度项去除,以高斯变异项替代,并在种群中随机选择一定数量的粒子采用上述更新公式进化,以提高多样性。文献[17]结合随机学习和列维飞行策略,在标准速度更新公式中增加一项,让种群粒子以列维随机步长向随机选择的粒子学习,在种群初始化后,当产生的随机数小于预设阀值时,使用标准PSO 公式更新种群,否则使用改进的公式更新种群。文献[18]在种群初始化阶段,采用反向学习策略随机初始化种群,取最优粒子作为初始种群,并对位置更新公式进行改进,在先前位置、速度项增加惯性权重,并让粒子向当前全局最优学习,惯性权重、加速因子服从正余弦函数变化,以提高收敛速度。
上述算法采用整体维度更新策略,同时更新粒子每一维,可加快种群收敛速度。但是,在粒子的进化过程中,全局最优值与普通粒子每一维的进化方向不总是一致,可能出现整体适应度值改善而粒子某一维退化,或粒子某一维改善而整体适应度值变差等问题。
针对上面所述问题,本文提出具有动态子空间的随机单维变异粒子群优化算法(stochastic single-dimensional mutated particle swarm optimization with dynamic subspace,SDMPSO)。为解决全局最优与普通粒子进化方向不一致问题,提出具有动态子空间的随机单维变异策略:从粒子的自身维度中随机不重复地挑选若干维度组成子空间,子空间随迭代次数的增加而减小,每次只随机选择异于子空间的一维进行变异,待变异的维度等于子空间内各维度的平均值。同时,提出Pareto 速度分配策略:在算法设定的前20%迭代次数内,增强种群的勘探能力,探索更多的新解空间区域,为后期的平衡搜索做准备;后80%迭代次数内,保持种群的勘探能力与开发能力平衡,使种群进行有效的平衡搜索。
2 标准PSO
粒子群优化算法将所求解空间位置,类比鸟群运动时栖息地。鸟群抽象为粒子群,鸟群间信息传递类比各粒子相互学习和信息共享的过程。运动过程中的状态信息对种群运动速度产生影响,实质为个体最优(pbest)和全局最优(gbest)控制粒子运动速度和方向,用数学形式实现该算法的过程如下。
设粒子数为N的种群,在维度为D的空间中搜索,粒子在解空间所处的位置可表示为xi=(xi1,xi2,…,xiD),i=1,2,…,N,代表第i个粒子的位置,每个xi都可由目标函数求得函数值f(xi)。vi=(vi1,vi2,…,viD),i=1,2,…,N,代表第i个粒子的速度。pbesti=(pbesti1,pbesti2,…,pbestiD),i=1,2,…,N,代表第i个粒子所经历的历史最优位置。gbest=(gbest1,gbest2,…,gbestD),代表整个种群的历史最优位置。粒子速度和位置可按照以下公式更新:
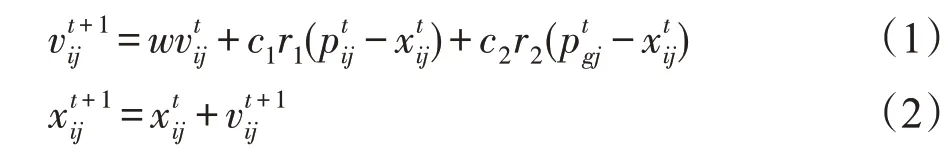
式中,惯性权重w控制粒子先前速度,平衡粒子局部和全局搜索能力,当w较大时,粒子的全局搜索能力较强,反之粒子的局部搜索能力较强。公式中c1、c2为学习因子(也叫加速因子),可使粒子具有自我学习和向其他优秀粒子学习的能力,快速向最优解靠近。r1、r2为(0,1)内的随机数为粒子i在第t次迭代时历史最优位置的第j维为第t次迭代时整个种群历史最优位置的第j维。
3 提出的新算法
3.1 Pareto速度分配策略
意大利经济学家Pareto 认为,在任何一组事件中,最重要的占其中一小部分,约20%,其余80%尽管是多数,却是次要的,这就是Pareto定律[19]。这种统计的不平衡性在社会、经济及生活中无处不在。由Pareto定律可知,分析或处理问题时不平均用力,要把80%的资源或精力用于求解占问题约20%的重要部分。
勘探与开发是种群进化的两个重要搜索能力。勘探能力强,种群能探索到更多解空间区域,提高寻得最优解的概率;开发能力强,种群可对最优解所在区域进行精细搜索,提高寻得最优解的精度。然而,当算法勘探能力强的阶段持续时间过长,易导致种群收敛速度缓慢或错过最优解;算法开发能力强的阶段持续时间过长,则易导致种群早熟收敛而陷入局部最优。因此,保持算法勘探与开发能力相等的平衡搜索,是算法优化性能提升的关键。而且,算法在未经过充分勘探,未获得更多新解空间区域的情况下,将降低平衡搜索的效率。
针对上述问题,根据Pareto定律指导算法在整个迭代过程的搜索状态。Pareto 定律的关键是明确问题的主要任务。从种群的搜索状态看,主要任务是保持勘探搜索与开发搜索的平衡。因此,依据Pareto定律,在算法设定的前20%迭代次数内,增强种群的勘探能力,探索更多的新解空间区域,为后期的平衡搜索做准备;后80%迭代次数内,保持种群的勘探能力与开发能力平衡,使种群进行有效的平衡搜索。上述过程可用如下公式实现:

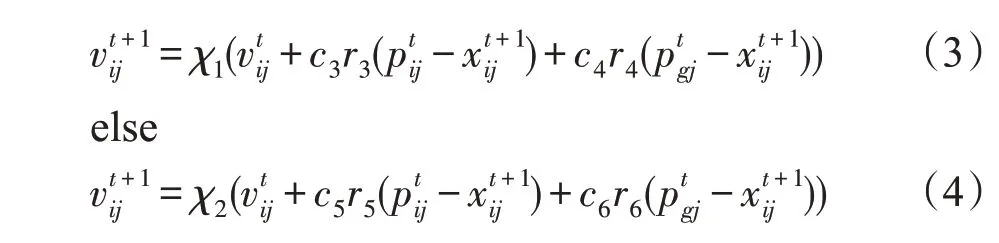
式中,t表示当前迭代次数,Max_t表示最大迭代次数。c3=2+exp(-t/Max_t)+0.5,c4=0.5-exp(-t/Max_t)+2.0为加速因子。为收缩因子。c5=c6=2,χ2=0.6,r3、r4、r5、r6为(0,1)间的随机数。
传统PSO 算法具有一些不良的动力学特性,特别需要限制粒子的速度以控制它们的轨迹[20]。因此,式(3)、式(4)引入收缩因子限制粒子的速度。文献[21]指出,自我认知项大于社会认知项,将导致搜索空间中的粒子过度徘徊。式(3)利用这一特性,使加速因子c3大于c4,增大自我认知项,使粒子能探索更广的解空间区域。为使粒子保持自我认知项等于社会认知项的平衡搜索,设置式(4)中加速因子c5等于c6。
3.2 具有动态子空间的随机单维变异策略
传统PSO 算法采用整体维度更新策略,粒子每一维的值同时更新。但是,全局最优值的进化方向与普通粒子每一维的进化方向不总是一致,将出现整体适应度值改善而粒子某一维退化,或粒子某一维改善而整体适应度值变差等问题。
为不失一般性,仍以最小为最优,当D=5 时,该函数的最优解为(0,0,0,0,0)。当在解空间中存在某个粒子的位置为xt(1,0,2,4,3)时,f(xt)=30,根据PSO 算法公式更新后,若粒子维度变为xt+1(0,4,0,4,0),此时f(xt+1)=32。由于f(xt+1)>f(xt),xt+1(0,4,0,4,0)将不会作为最优解保留。相比xt的维度值,xt+1的第1、3 和5 维都有较大改善,但仅因第2 维退化而使整个粒子的适应值变差。
针对此问题,提出具有动态子空间的随机单维变异策略:从粒子的自身维度中,随机不重复地挑选若干维度组成子空间,子空间的大小随迭代次数的增加而逐渐减小,每次只随机选择异于子空间的一维进行变异,其值等于子空间内各维度的平均值。具体可用下式表示:
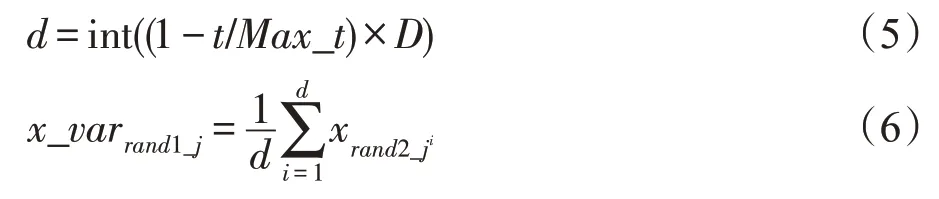
式(5)中,int 表示取整函数,t表示算法当前迭代次数,Max_t表示最大迭代次数,d∈(1,2,…,D-1)为子空间内的总维度数。式(5)表示子空间内的总维度数d随迭代次数的增加而减少。式(6)中,rand1_j∈D为维度D内随机选择的一维。rand2_ji为进行第i次随机不重复的挑选时,从粒子维度D内挑选的第rand2_j维,rand1_j≠rand2_ji。式(6)表示只随机选择粒子异于子空间的一维进行变异,其值等于子空间内各维度的平均值。
通过单维变异的方式,使某一维的进化不影响其他维。同时,单维变异没有破坏粒子群的整体结构,不影响粒子群正在进行的局部精细搜索。粒子进化到后期,只有某一维或某几维未达到最优解,单维变异可针对某一较差维度进行变异,能有效地提升收敛速度并得到更高质量解。
3.3 新算法原理
种群粒子在进化过程中,追随个体最优(pbest)和全局最优(gbest)运动,个体最优代表种群进化到当前代时最优的位置群体,全局最优从个体最优中产生。本文提出的具有动态子空间的随机单维变异策略,从粒子自身维度中,随机选取若干维度组成子空间,粒子拥有优质的维度值,对变异产生高质量解至关重要。
因此,为保证进行变异粒子的维度质量,本文选择所有个体最优和全局最优粒子进行变异。具体可用下式表示:
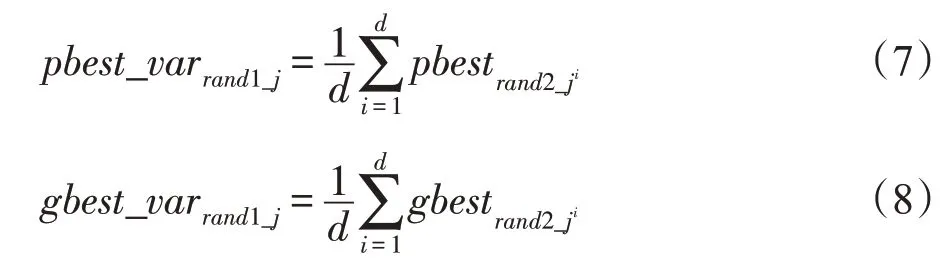
在算法求得个体最优和全局最优后,分别对这两类优质粒子进行变异,增强种群的多样性。该策略随机选择pbest和gbest的某一维进行变异,“随机”的不确定性,可能导致原优质维度值被舍弃,替换成变异后的低质量维度值。pbest和gbest变异后,直接通过自我认知项和社会认知项影响粒子速度。因此,本文的速度更新公式,选择具有收缩因子的式(3)和式(4),作为新速度更新模型,收缩因子同时控制先前速度项、自我认知项和社会认知项。文献[12]指出,当随机性被引入具有收缩因子的完整模型时,随机性带来的有害影响将被控制。新算法运行步骤可用如下伪代码表示。

4 算法分析
4.1 Pareto速度分配策略分析
算法依据Pareto定律,在算法设定的前20%的迭代次数内,增强种群的勘探能力,探索更多的新解空间区域,为后期的平衡搜索做准备;后80%的迭代次数内,保持种群的勘探能力与开发能力平衡,使种群进行有效的平衡搜索。
为验证采用Pareto速度分配策略,能更有效地提高算法的优化性能,记该速度分配策略为2/8,将其与速度分配策略分别为1/9、3/7、4/6、5/5、9/1、8/2、7/3、6/4、1/0 和0/1 的策略进行比较,实验选取12 个常用的测试函数Sphere(f1)、Schwefel's P2.22(f2)、Schwefel's P1.2(f3)、Schwefel's P2.21(f4)、Rosenbrock(f5)、Step(f6)、Quartic(f7)、Schwefel's P2.26(f8)、Rastrigin(f9)、Ackley(f10)、Griewank(f11)、Penalized1(f12),在维度D=30,评估次数为20万次的条件下进行比较,算法独立运行30 次,Mean 表示30 次运行的最优解平均值,Std表示标准差,所得结果见表1所示。
表1 中,本文采取的2/8 策略在5 个函数上取得最优解,在另两个函数上取得的Mean比其他策略更优,将各策略最优解平均值进行Friedman检验,所得表2 中2/8 策略下秩均值最小(4.33),验证了该策略能更有效提高算法的优化性能。
4.2 动态子空间策略分析
粒子进化前期,多数维度未到达最优解位置,存在少数离最优解较近的维度;在进化后期,若粒子陷入局部最优,其多数维度已到达最优解位置,只存在少数未到达最优解位置的维度。为证明此现象,对标准PSO 算法在10 维条件下,对Shifted and Rotated Schwefel’s Function 进行测试,迭代次数为2 500 代,可行域[-100,100]。选种群当前最优粒子(gbest)为研究对象,记录其在100和2 400代的维度信息,绘制成图1和图2。
图中横坐标D_1~D_10 表示gbest的10 个维度,纵坐标表示各维度的维度值,柱状图为gbest所得各维度的具体数值,折线为函数在各维度的最优值(optimum)。由图1和图2可知,gbest在100代时,第1、4、5 和第7 维离最优解位置相对较近,其他维度相对较远;gbest在2 400 代时,第1、2、3、4、5、7、8 和第10维离最优解位置相对较近。
因此,本文采取的策略中,子空间大小动态变化,在粒子进化前期选取多数维度组成子空间,增大变异维度的多样性,使粒子探索更多新区域;后期选取少数维度组成子空间,使维度变异不过于激进,增强粒子精细搜索的能力。
为验证动态子空间策略能更有效平衡勘探与开发能力,将其与子空间大小固定的策略进行比较,在维度D=10 的条件下,分别固定1,2,…,10 维作为子空间大小,与动态子空间策略在12 个常用测试函数上进行比较,评估次数设为10万次。为方便书写,记动态子空间策略为Dyn_D,子空间大小固定的策略分别记为D_1~D_10,各策略独立运行30 次,结果见表3所示。
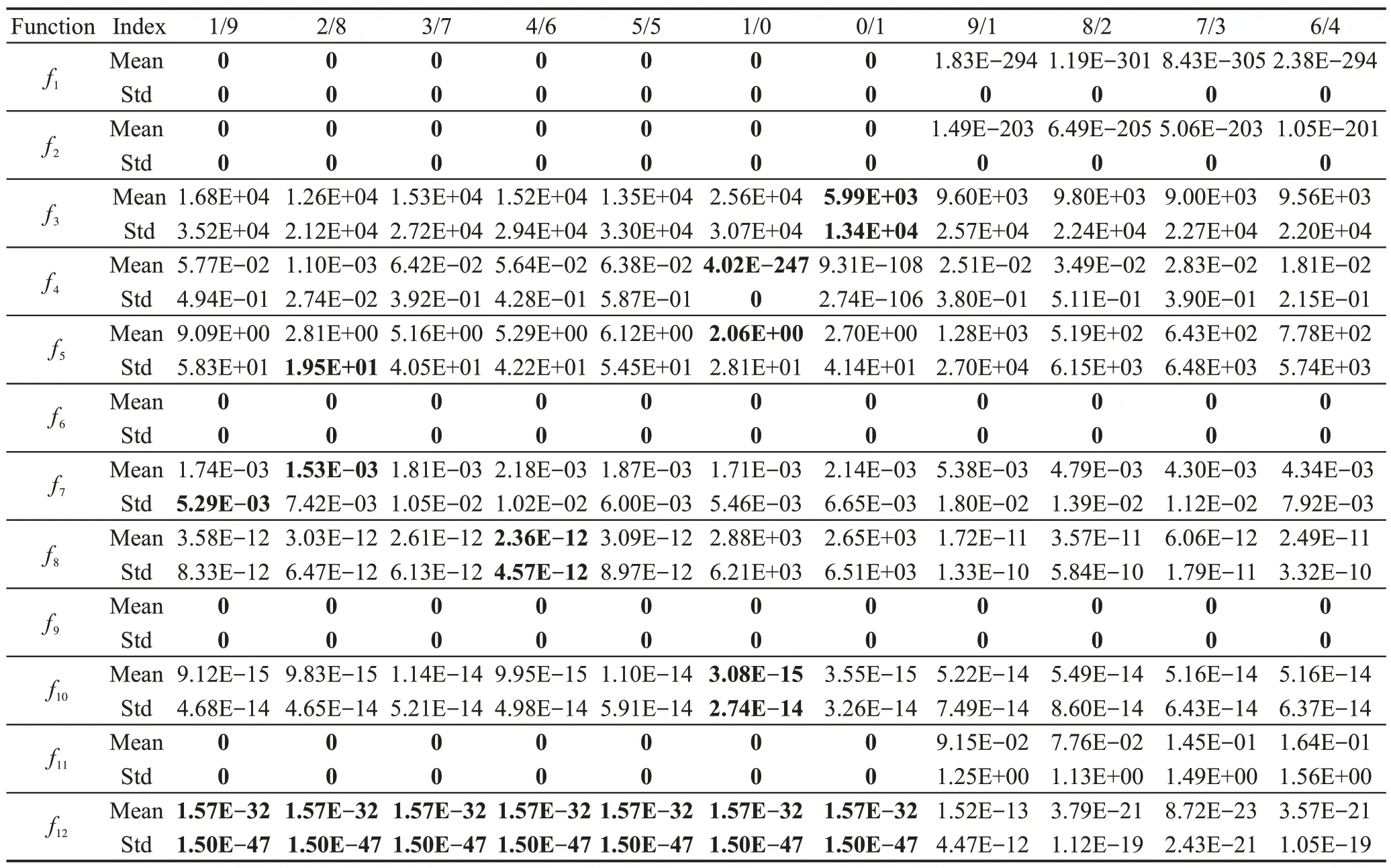
Table 1 Speed allocation strategy test results表1 各速度分配策略测试结果
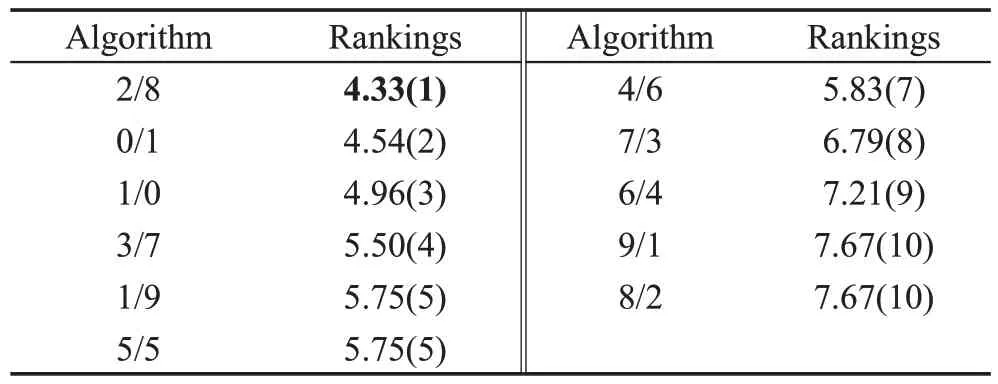
Table 2 Friedman test result表2 Friedman 检验结果
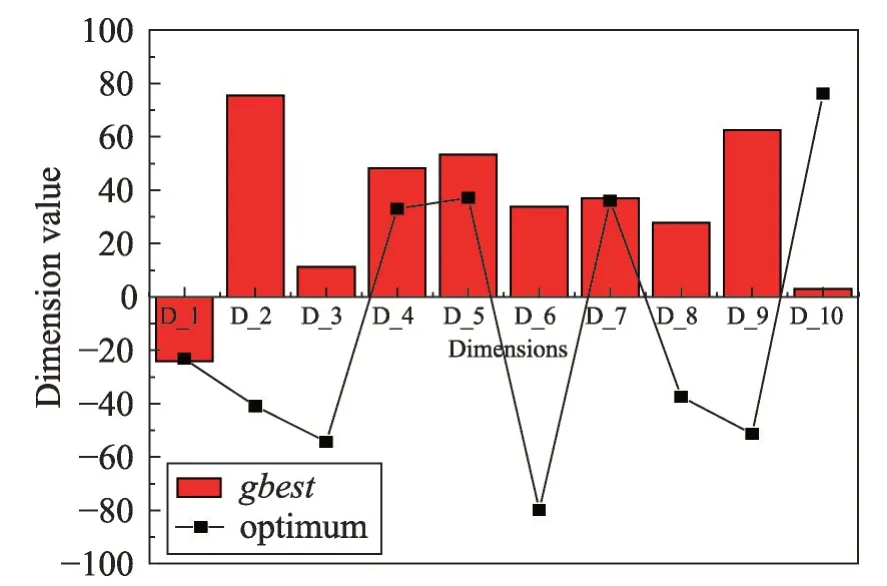
Fig.1 Dimension value in 100 generations图1 100代时维度值
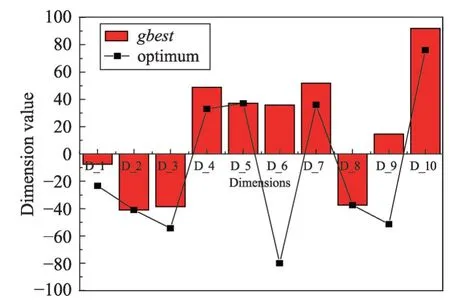
Fig.2 Dimension value in 2400 generations图2 2 400代时维度值
动态子空间策略与其他10种子空间大小固定的策略相比,在7 个函数上取得的最优解更优,将表4中所得平均值进行Friedman 检验,动态子空间策略所得秩均值最小(5.21),验证了本文采用动态子空间策略的综合优化性能更强。
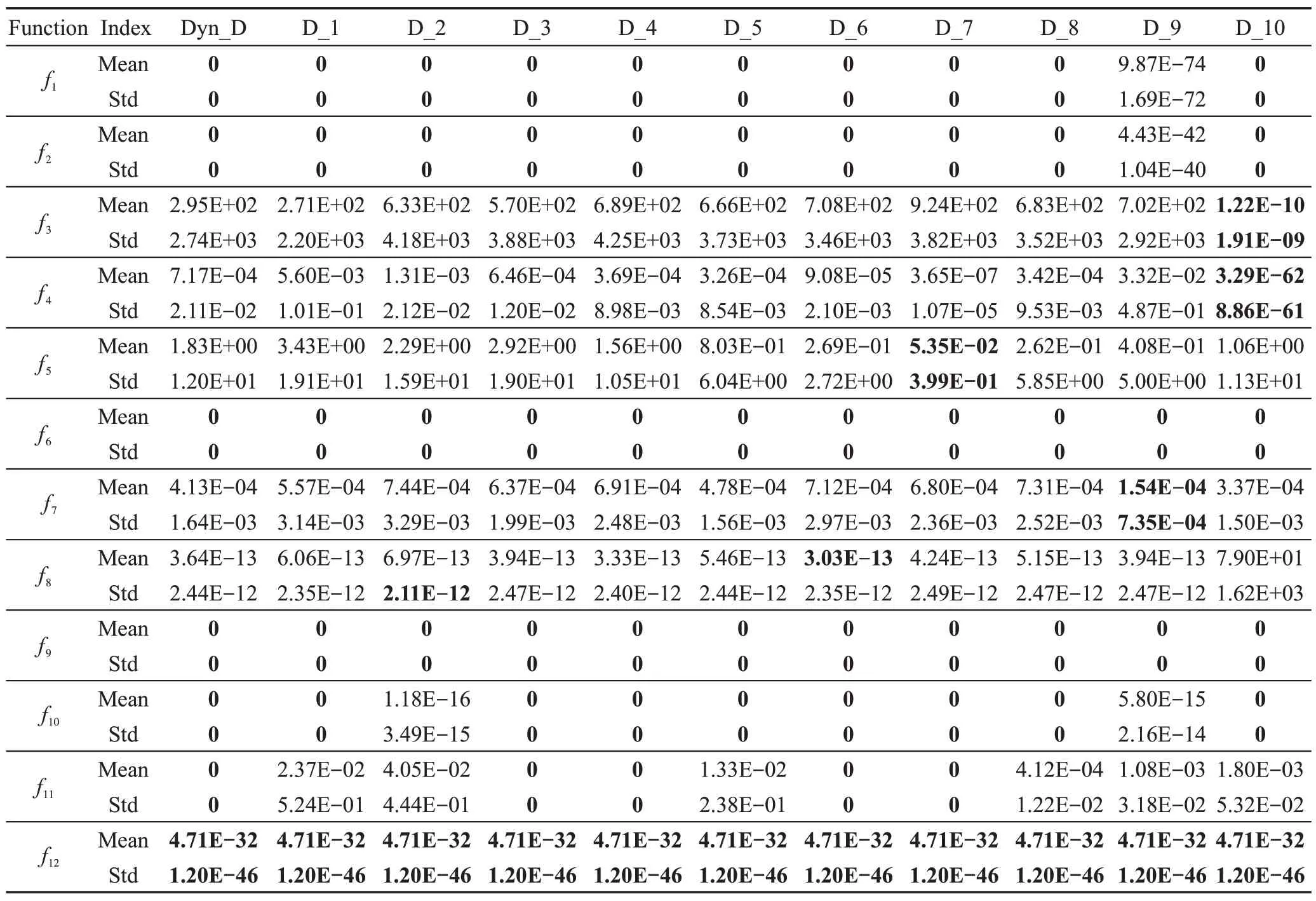
Table 3 Comparison results between dynamic subspace and fixed subspace strategy表3 动态子空间与固定子空间策略比较结果
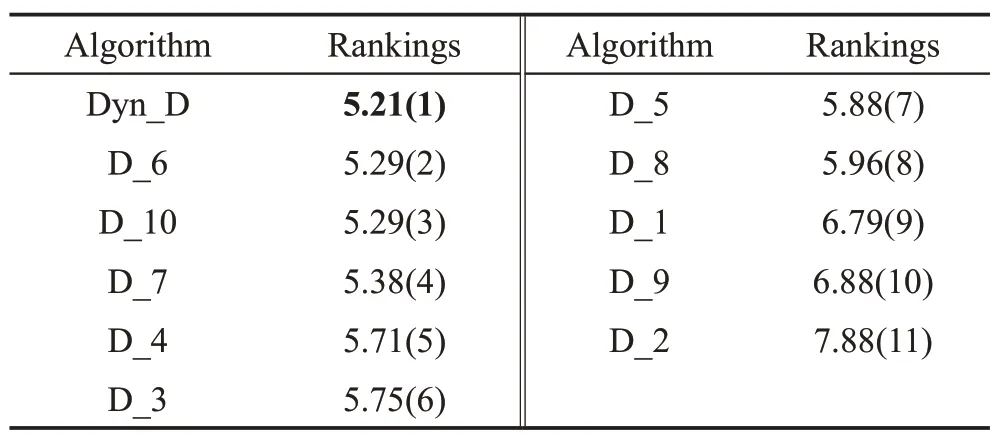
Table 4 Friedman test result表4 Friedman 检验结果
5 仿真实验
5.1 测试函数与参数设置
引入26 个基准函数进行仿真实验,函数分为4类:f1、f2、f4、f15、f16、f17、f18、f19和f20为单模函数,f3在低维时为单模函数,高维时为多模函数;f5、f6、f7、f8、f9、f10、f21、f22、f23、f24、f25和f26为多模函数;f11、f12、f13和f14为旋转函数。表5中列出了26个测试函数的基本信息。本文算法(SDMPSO)的参数设置如下:种群规模N设置为20,Max_t表示最大迭代次数,t表示当前迭代次数。在种群进化的前20%×Max_t的迭代次数内,加速因子c3=2+exp(-t/Max_t)+0.5,c4=0.5-exp(-t/Max_t)+2.0,收缩因子在后80%×Max_t的迭代次数内,加速因子c1=c2,收缩因子χ3=0.6。各对比算法的参数设置参照文献[20]。
5.2 数值仿真实验
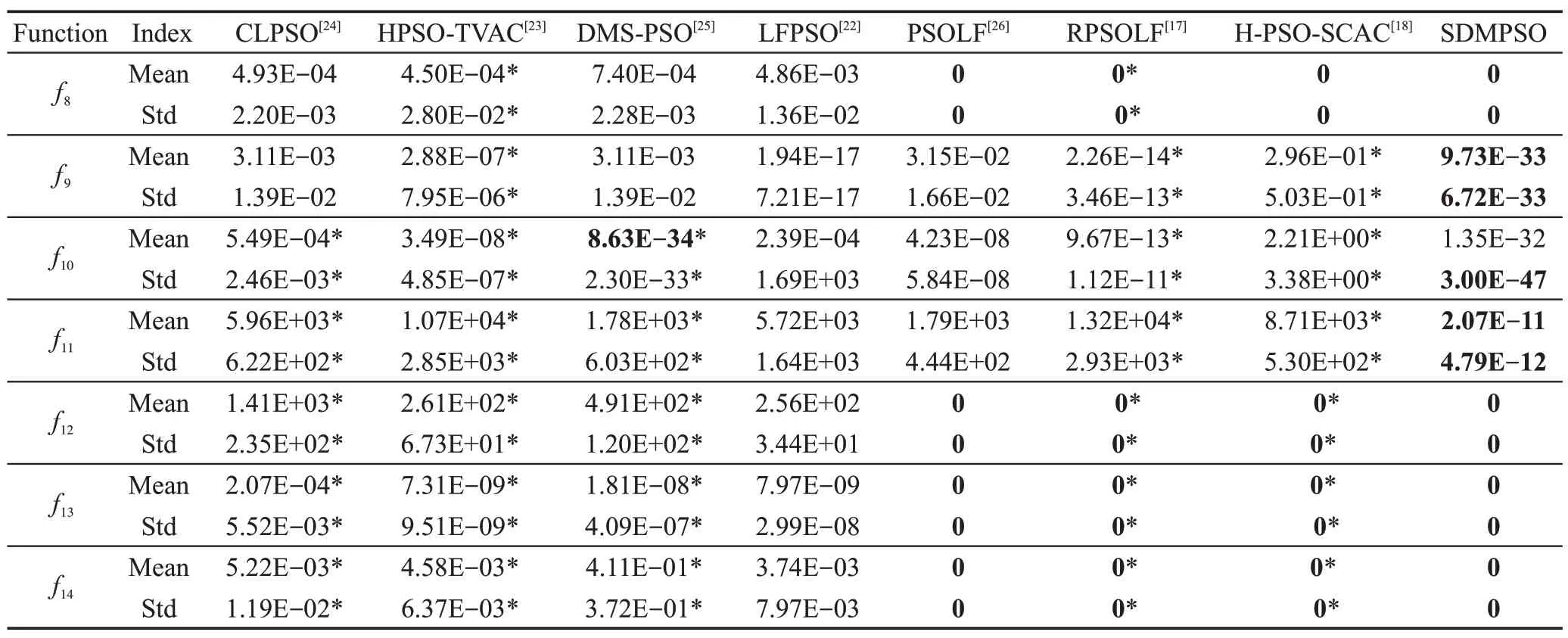
将SDMPSO 再与7 种知名PSO 改进算法分别在维度D=30,50,100 的条件下对比,这7 种算法分别为LFPSO(particle swarm optimization algorithm with Levy flight)[14]、RPSOLF(particle swarm optimization algorithm with random learning mechanism and Levy flight)[17]、H-PSO-SCAC(hybrid particle swarm optimizer with sine cosine acceleration coefficients)[18]、HPSO-TVAC(self- organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients)[21]、CLPSO(comprehensive learning particle swarm optimizer)[22]、DMS-PSO(dynamic multi-swarm particle swarm opt-imizer)[23]、PSOLF(particle swarm optimization with Levy flight)[24]。各算法的参数都按照原文献设置,当D=30 时,评估次数设为20 万次;D=50 时,评估次数设为25 万次;D=100 时,评估次数设为50 万次。所有算法独立运行30 次,最终结果取30 次的平均值,具体实验数据见表6~表8所示,表中Mean表示平均最优适应值,标准差用Std 表示,最好值在表中用粗体标示。

Table 5 Benchmark function表5 测试函数

续表
表6~表8 中实验数据来源如下:CLPSO、DMS-PSO 在维度为30、50、100 时,所测试函数f1、f2、f3、f4、f6、f7、f8、f9和f10的数据引自文献[25];f5、f11、f12、f13和f14在30、50 维的数据引自文献[17]和文献[26]。HPSO-TVAC 在30 维的数据引自文献[17]。LFPSO、PSOLF 在30、50 维的数据引自文献[24];PSOLF 在100 维时,f1、f2、f3、f4、f6和f8的数据引自文献[24]。RPSOLF 在30 维时数据引自文献[17]。H-PSO-SCAC在30和50维时,f3、f4、f6、f7、f8的数据引自文献[18]。表中剩余未提及的函数数据,原文献未进行测试,为笔者按文献的思路实现所得,并在表中用“*”在数据右上角标示。
分析表6~表8数据,得出以下结论:
(1)SDMPSO算法性能分析
在相同评估次数下,SDMPSO算法在D=30、50、100 维时,所测函数f1、f2、f6、f8、f12、f13和f14全部求得最优解,所测函数f9和f10同样求得比其他算法更高质量的解,测试f3、f4和f5函数所得最优解相比其他算法优势明显。虽测试维度升高,算法仍能保持较好优化性能。
(2)其他算法优化性能分析
CLPSO 在测试函数f5时优势明显,测试其余函数时,在30 维能够取得较好质量解,但在50、100 维时算法性能有待加强。CLPSO主要借助不同的个体最优(pbest)优势信息产生最优解,但因其在搜索过程中种群常更新停滞,早熟收敛仍是CLPSO 需解决的问题。
HPSO-TVAC算法引入时变的加速因子控制“社会认知”和“自我认知项”,但当进化后期粒子聚集时,难以逃离局部最优。DMS-PSO 算法将种群中粒子分为多个子种群,通过各子种群的信息交流以平衡算法勘探与开发能力,但各子种群的协作能力仍有待提高。HPSO-TVAC 和DMS-PSO 在测试函数f9、f10时优势明显,测试其余函数时,上述算法在低维时能求得较好质量的解,在高维搜索时算法易陷入局部最优。
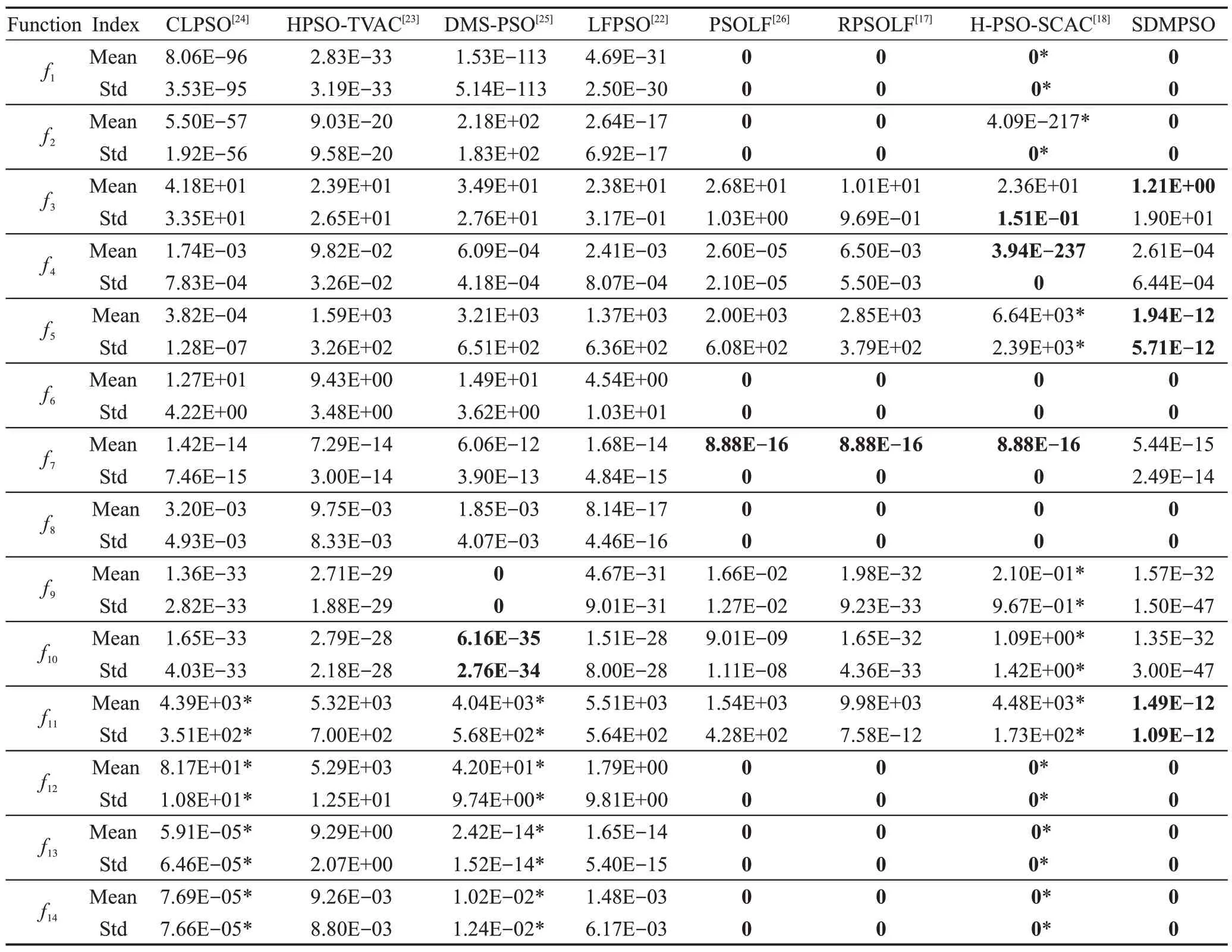
Table 6 30-dimensional test results表6 30维的测试结果
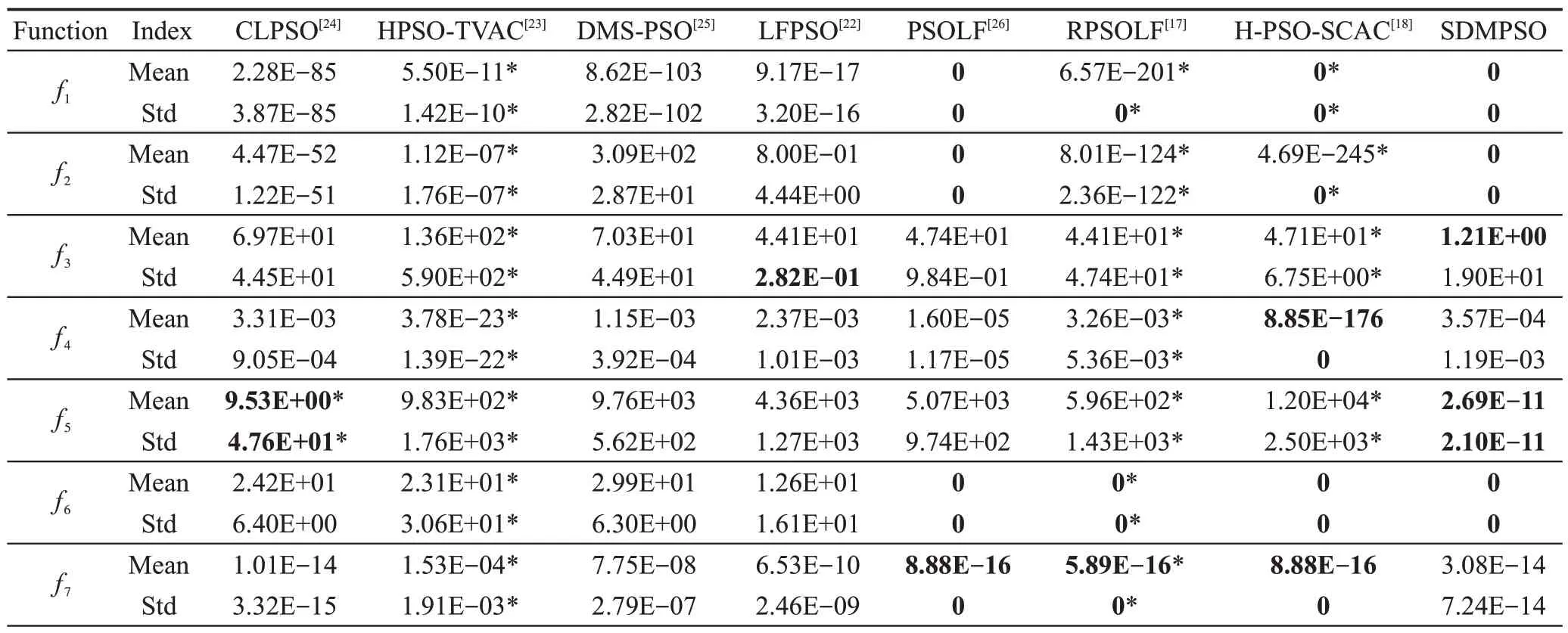
Table 7 50-dimensional test results表7 50维的测试结果
续表
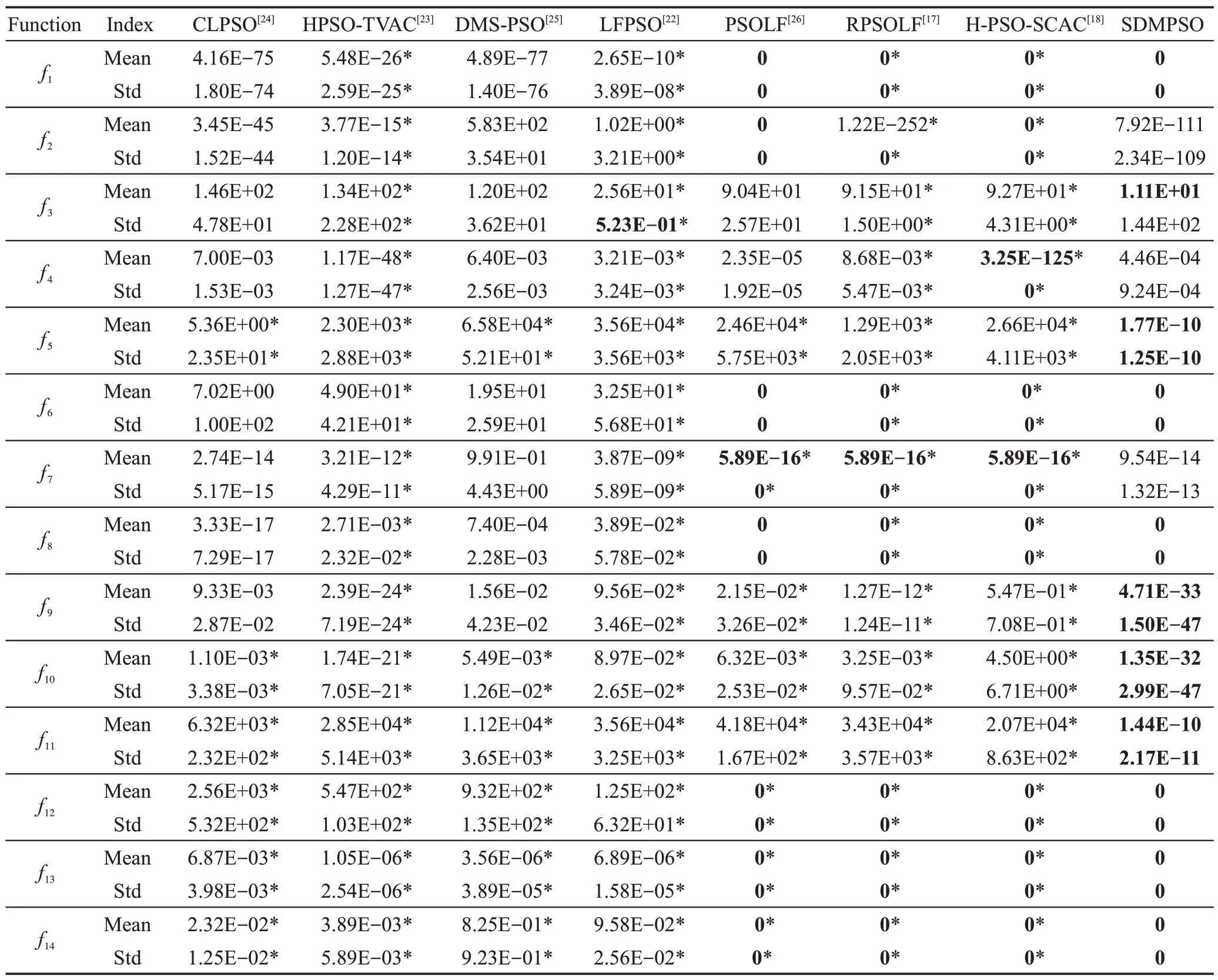
Table 8 100-dimensional test results表8 100维的测试结果
LFPSO、PSOLF、RPSOLF都采用列维飞行策略,使种群增加随机步长,其中LFPSO 使种群粒子绕着最优解做列维飞行,在算法后期种群易更新停滞,故LFPSO 在低维时测试单模和多模函数,搜索到最优解的质量较高,但在高维仍易陷入局部最优。PSOLF 和RPSOLF 则另增加了随机选择策略,在一定概率范围内使用列维飞行策略,在测试函数f1、f2、f6、f8、f12、f13和f14时求得函数最优解,但在高维条件下测试f9、f10时算法仍陷入局部最优。
H-PSO-SCAC采用sin、cosine函数控制加速因子的变化,并在使用反向学习初始化种群后,采用改进的速度更新公式,其在优化函数f4时,能够取得较高质量的解,在函数f1、f2、f6、f8、f12、f13、f14同样求得函数最优解,但在测试函数f9和f10时,算法仍陷入局部最优。
(3)各算法性能统计分析
为进一步综合评价SDMPSO 算法的性能,引入Friedman 检验分析所得测试数据,秩均值作为Friedman 检验的评价参数,该值越小,表明算法的性能更优。表9 给出各算法数据经Friedman 检验后的秩均值,并在小括号内给出其在所有算法中的排名。表中SDMPSO 算法在维度D=30、50 和100 维时,所得秩均值最小,故该算法性能更优。H-PSO-SCAC、RPSOLF、PSOLF 算法在维度逐渐增高时,其在多数函数上都能保持较好的优化性能,在少数复杂多模函数上,优化性能逐渐下降。CLPSO、HPSO-TVAC、DMS-PSO、LFPSO 算法在维度逐渐增高后,各算法在测试函数上的优化性能逐渐下降。
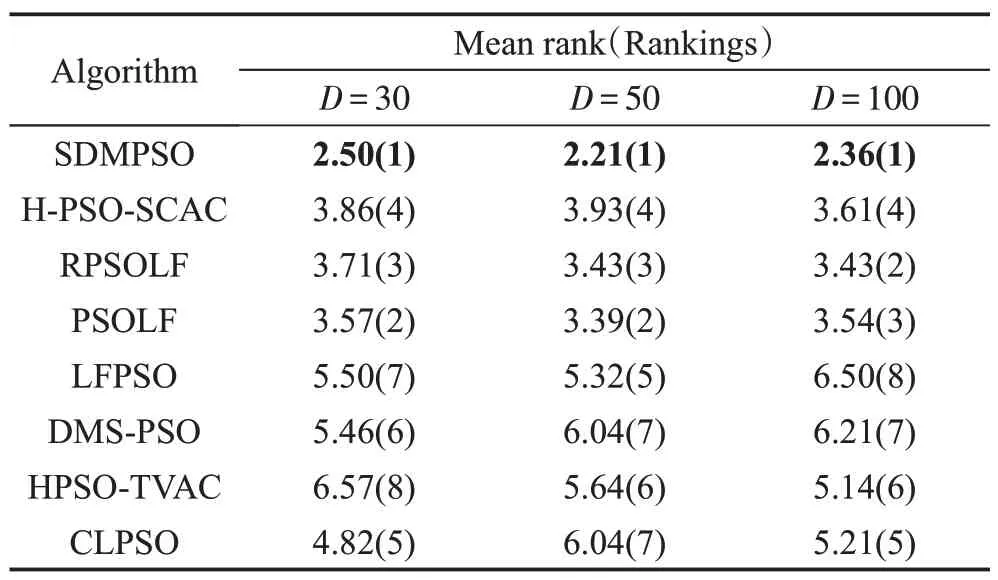
Table 9 Friedman test result表9 Friedman 检验结果
在Wilcoxon检验中,P-values小于0.05则表示两对比算法存在显著差异。表10 显示,SDMPSO 在30、50 和100 维时,显著优于CLPSO、HPSO-TVAC、DMS-PSO和LFPSO。
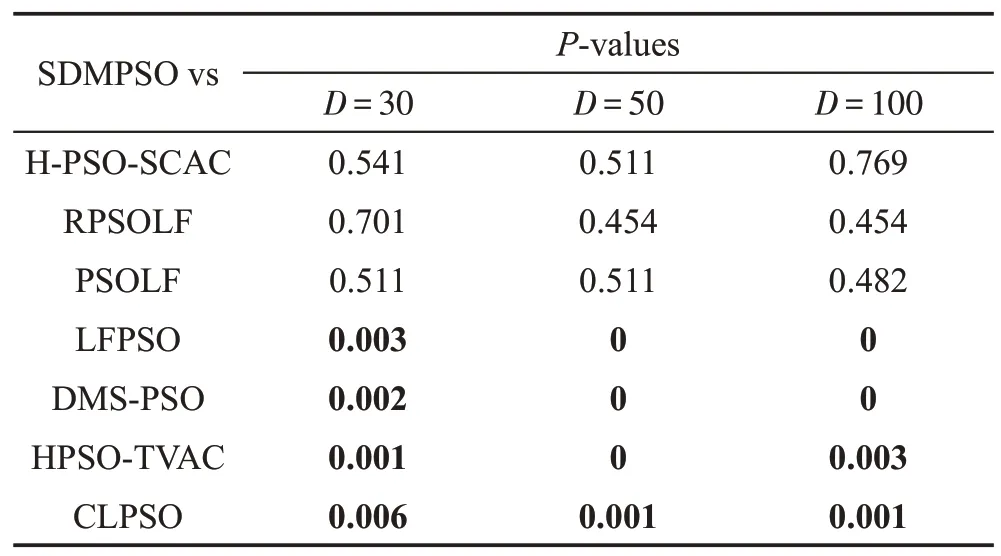
Table 10 Wilcoxon test result表10 Wilcoxon 检验结果
5.3 收敛性分析
图3(a)~图3(n)中,在维度为30,评估次数20万次的条件下,对SDMPSO 算法与CLPSO、HPSO-TVAC、DMS-PSO、LFPSO、PSOLF、RPSOLF 和H-PSO-SCAC算法,在函数f1~f14优化过程中的收敛性能进行分析,图中横坐标FEs 表示评估次数,Fitness 表示算法所得适应值。
在单模函数Sphere、Schwefel2.22 上,所有算法在Sphere 函数上都能够求得较高精度解,但SDMPSO 算法求得最优解所用评估次数更少,收敛速度最快。在Schwefel2.22 上,DMS-PSO 算法未能求得最优解,其余算法能求得较高精度解,但消耗的评估次数比SDMPSO算法多。
在单模函数Rosenbrock、Quartic上,H-PSO-SCAC的优化性能突出,能求得比其他算法更高精度解。SDMPSO 算法相比其他算法,收敛到较有优势的解且收敛速度较快。
在多模函数Schwefel2.26上,CLPSO的优化性能相比其他算法优势明显,所求解的精度最高,收敛速度最快。SDMPSO对此函数的优化能力相比其他函数较有优势。
在多模函数Rastrigin、Ackley、Griewank 上,SDMPSO、PSOLF、RPSOLF 和H-PSO-SCAC 都能求得最优解,SDMPSO相比其他算法在收敛速度上,有较大优势。其余算法收敛速度慢,且收敛精度低。
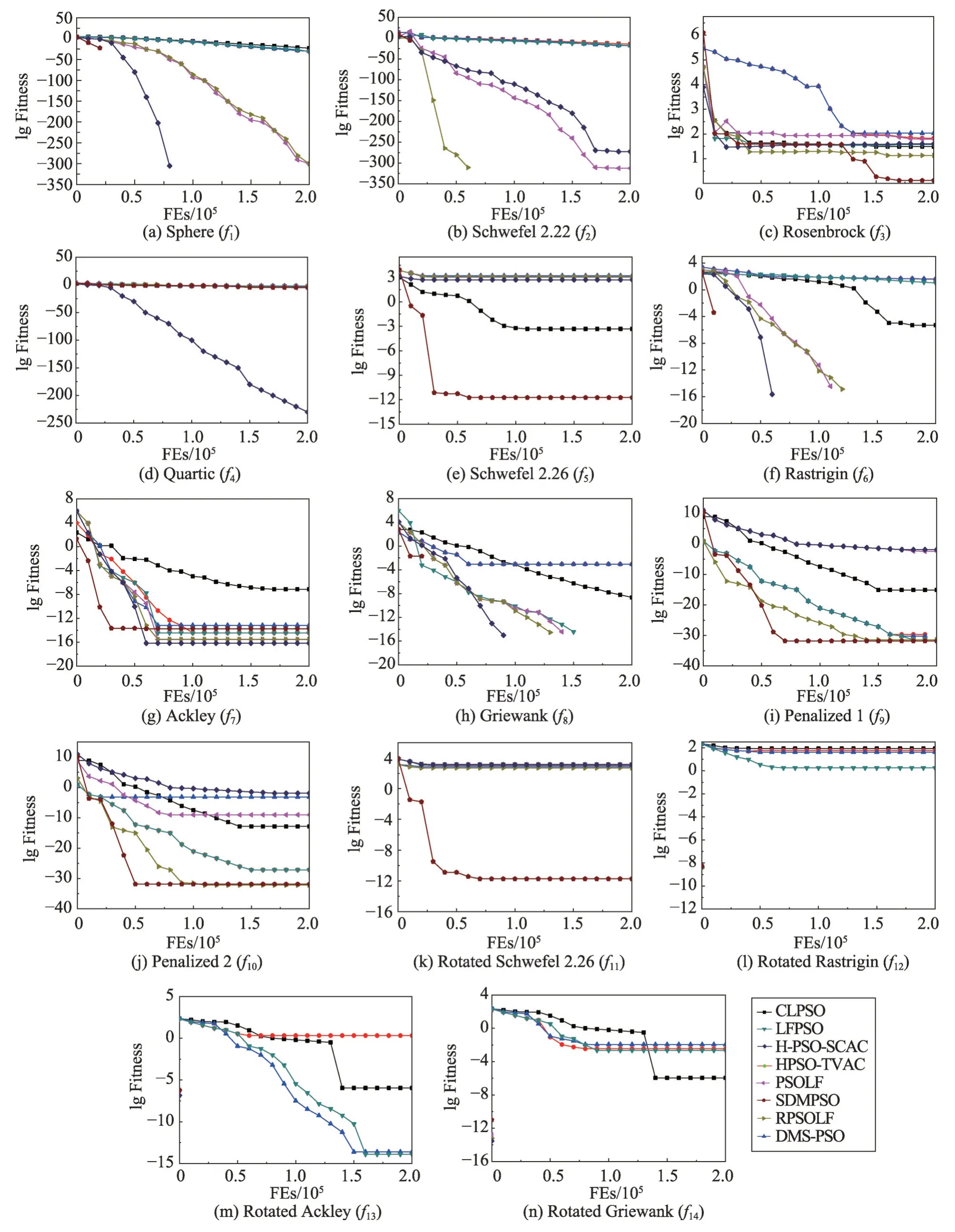
Fig.3 Graph of function convergence图3 函数收敛曲线图
在多模函数Penalized1、Penalized2 上,H-PSO-SCAC 和PSOLF 收敛精度较低,其他算法能够收敛到较高精度的解,SDMPSO算法的收敛速度更快,精度更高。
在旋转函数Rotated Schwefel2.26 上,PSOLF 的收敛精度最高,SDMPSO 相比其他算法收敛速度和精度有较大优势。在旋转函数Rotated Rastrigin、Rotated Ackley、Rotated Griewank 上,SDMPSO、PSOLF、RPSOLF 和H-PSO-SCAC 都能求得最优解,SDMPSO 在收敛速度上优势明显,其余算法未能求得最优解。
5.4 与相关新算法比较
近年来,在智能计算领域,另提出了许多较有优势的算法[27],且已成功应用于工程实践。人工蜂群算法(ABC)是Karaboga受蜜蜂觅食启发,于2005年提出的新智能算法,该算法具有较好的勘探能力,在解决高维和多模问题时优势明显。文献[28-29]在多组不同特性的Benchmark函数上,将ABC算法与主流的智能算法遗传算法(genetic algorithm,GA)、差分进化算法(differential evolution,DE)和PSO 等算法进行比较,结果表明ABC算法在处理复杂多模函数上性能更优。
ABC 算法每次只选择父代的一维进行变异,本文算法同样采用单维变异的策略得出新的粒子位置。因此,为进一步验证算法的优化性能,选取新改进的人工蜂群算法:GABC(gbest-guided artificial bee colony algorithm)[30]、qABC(quick artificial bee colony algorithm)[31]、best-so-far ABC(best-so-far selection in artificial bee colony algorithm)[32]、dABC(directed artif-icial bee colony algorithm)[33]、MABC(modified artificial bee colony algorithm)[34]和MPGABC(modified Gbest-guided artificial bee colony algorithm)[35]算法在22 个基准测试函数上进行比较,测试维度为100 维,评估次数为500 000次。所有算法独立运行25次,最终结果取25次的平均值,具体实验数据见表11所示,表中Mean为平均最优适应值,标准差用Std 表示,最好值在表中用粗体标示。表中数据来源和参数设置参考文献[35]。
分析表11数据,得出以下结论:
(1)SDMPSO算法性能分析
在D=100 维时,算法所测函数f1、f6、f8、f19、f21和f20全部求得最优解,在f2、f4、f9、f15、f16、f18、f20、f23、f24和f25函数上同样求得高质量解,其余函数相比其他算法也有较大优势。
(2)其他算法优化性能分析
在D=100 维时,GABC在函数f6、f19、f21、f25和f26上全部求得最优解,在f5和f20函数求得高质量解,其余函数上优化性能较好。qABC、best-so-far ABC 和dABC 在函数f19、f25和f26上全部求得最优解,在f20函数上求得解质量较高,对其余函数的优化性能有待加强。MABC 在函数f19、f6、f21、f24、f25和f26上取得最优解,在f7、f9、f10、f20和f23函数上取得高质量解,其余函数上求得解优势较大。MPGABC 在函数f6、f19、f21、f25和f26上求得最优解,在f3、f9、f10、f17、f20和f23函数上求得解质量较高,其余函数上求得解优势明显。
(3)各算法性能统计分析
对表11 中所得数据进行Friedman 检验分析,表12 列出各算法数据经Friedman 检验后的秩均值,并在小括号内给出所有算法的排名。表中,SDMPSO算法在维度D=100 维时,所得秩均值最小,故该算法综合优化性能更强。在Wilcoxon检验中,P-values小于0.05则表示两对比算法存在显著差异。表12中显示SDMPSO在100维时,显著优于qABC和dABC算法。
群智能算法经过近几年的大量研究,绝大多数改进算法对较早版本的基准测试函数有较好优化效果。因此,本文采用新近提出的测试函数CEC 2015[36]进一步验证算法的优化性能,其包含的15 个测试函数中,所有函数在各个维度的最优解都不相同。将SDMPSO分别与新近提出的改进萤火虫算法VSSFA(variable step size firefly algorithm)[37]、WSSFA(wise step strategy for firefly algorithm)[38]、萤火虫与粒子群混合优化算法(hybrid firefly and particle swarm optim-ization algorithm,FFPSO)[39]比较,维度D=30,评估次数为1 500。
表13为各算法在CEC 2015测试函数上,独立运行30次后所得平均最优适应值。SDMPSO算法在所测15 个函数中,有6 个函数占较大优势。表14 对各算法进行Friedman 检验,SDMPSO 算法所得秩均值最小,再次验证SDMPSO 对新测试函数同样具有较好优化效果。
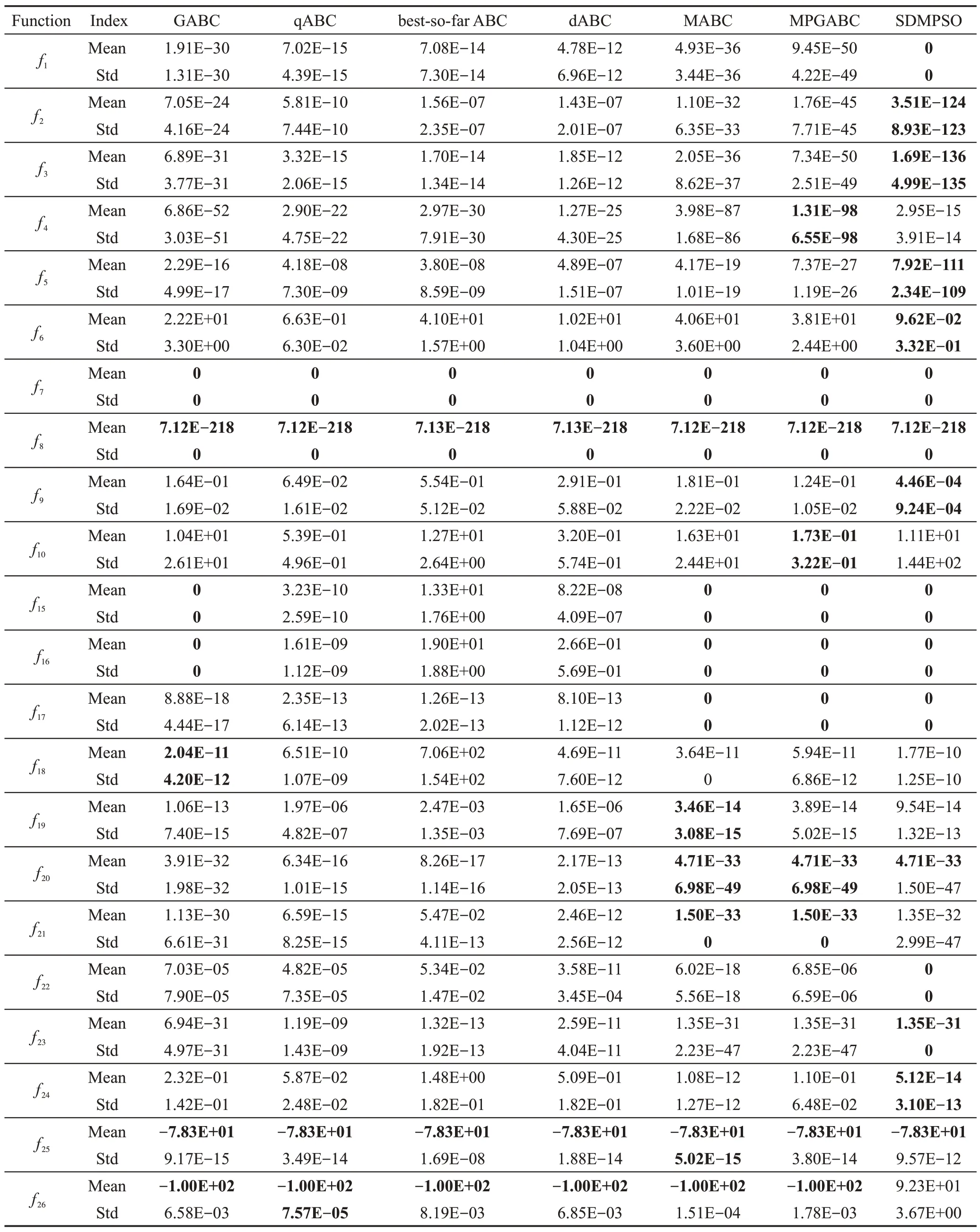
Table 11 100-dimensional data表11 100维数据
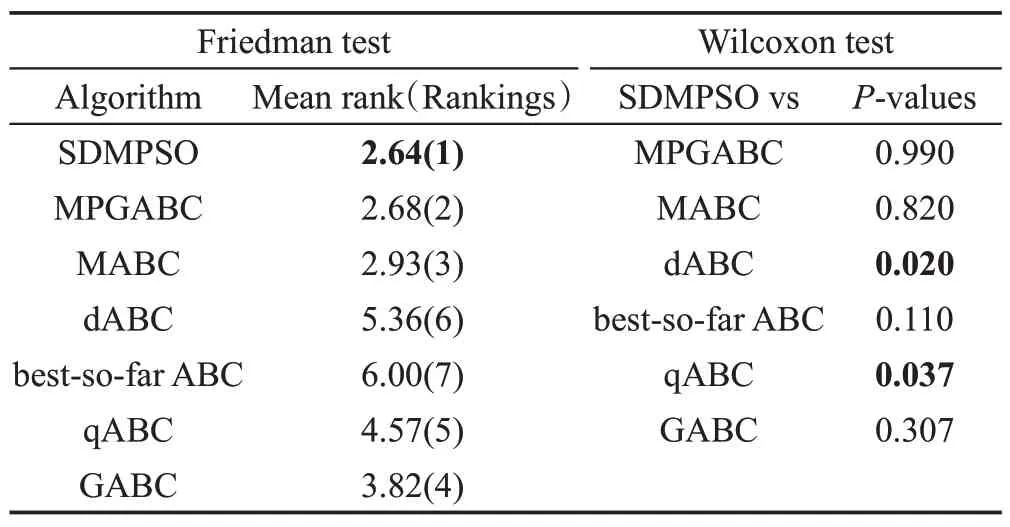
Table 12 Result of Friedman and Wilcoxon test表12 Friedman和Wilcoxon检验结果
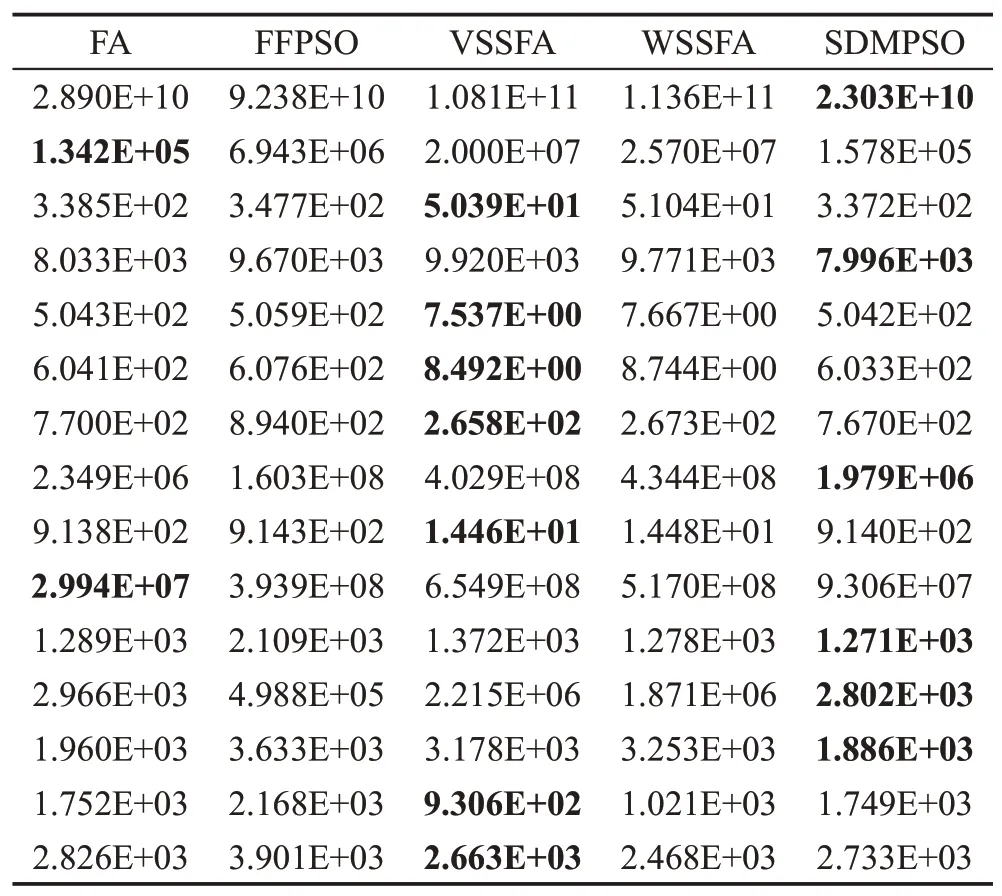
Table 13 Mean optimum of CEC 2015 experiment表13 CEC 2015 平均最优适应值

Table 14 Result of Friedman test表14 Friedman检验结果
6 结束语
针对粒子群算法采用整体维度更新策略,易存在某一维或某几维未达到最优解而导致粒子整体适应值变差等问题。本文主要提出两种改进策略:(1)提出Pareto 速度分配策略控制算法在整个迭代过程的搜索状态,在前20%的迭代次数内,探索新解空间区域,为后80%迭代次数内进行平衡搜索做准备,提高搜索的效率。(2)提出具有动态子空间的随机单维变异策略,每次只随机选择粒子的一维进行变异,其值等于子空间内各维度的平均值。通过子空间的动态调整,得到高质量的变异值,改善粒子的整体维度质量。
将本文算法在30、50 和100 维的条件下,与新近改进的高水平粒子群算法在单模、多模和旋转函数上进行比较。数值实验结果表明,本文算法在收敛精度和收敛速度上高于其他粒子群算法。同时与改进的人工蜂群算法和萤火虫算法进行比较,实验结果同样表明本文算法优化性能更强。但是,算法在处理某些高维复杂函数时仍易陷入局部最优。因此,在下一步的研究工作中,将在挑选变异的维度方面,可提出新的策略替代随机挑选的方式,进一步提高变异的效率。

