一种基于时间戳的简单表缩减算法∗
杨明奇 , 李占山 , 张家晨
1(吉林大学 计算机科学与技术学院,吉林 长春 130012)
2(符号计算与知识工程教育部重点实验室(吉林大学),吉林 长春 130012)
约束传播(或局部相容性)作为一种有限的推理方法[1],被广泛应用于求解约束满足问题.目前比较成功的一种方法是将回溯搜索与约束传播相结合,在预处理以及回溯搜索的每一阶段删除不满足相容性的赋值来降低搜索空间.局部相容性根据用于推理的约束子网的规模可以分为不同强度的相容性,通常,更强的相容性意味着更强的剪枝能力和更高的实现复杂度,而广义弧相容(generalized arc consistency,简称GAC)是研究最多且应用最广泛的局部相容性方法.
近年来,在配置、数据库、偏好建模等领域有着重要应用的表约束求解方法受到了大量学者关注.表约束上的弧相容算法研究诞生了许多成功的技术,其中,simple tubular reduction(STR)[2]是一种可以动态维持元组集有效部分的算法.STR 使用一种简单的数据结构sparse set[3,4]表示元组的序号,具有增量维持元组集的有效部分以及单位时间的回溯代价的性质.STR2[5]对STR 提出两点改进:(1)只对相邻两次调用中元组对应变量论域发生改变的位置检测有效性,实现了增量检测元组有效性;(2)当变量中所有值均找到支持时,停止为该变量查找支持,避免了无用的支持查找.STR3[6]类似GAC4 是路径最优的,通过查询dual table,找到并删除无效值对应的无效元组,再通过被删除的无效元组为其他变量值更新支持.这避免了STR2 中可能存在的对约束表同一区域的重复查找,但dual table 中需要处理的元组数目是原始表中约束元数的倍数,当约束元数较高时,同样会存在较多重复的查找,路径最优方法对于能否提升维持GAC 的效率并不明确.例如,在多数实例上,STR2 的效率优于STR3[7,8].AdaptiveSTR[9]给出了一种自适应的表缩减方法,可以根据当前约束表中有效部分的规模,自适应地选择代价较低的表缩减策略.文献[10]改善了STR2 在有效元组集缩减较慢时的性能.
将元组集压缩表示可以降低待处理的元组集的规模,也是一种有效的提高维持GAC 效率的方法,并受到了深入的研究.其中,MDD 算法[11]将每个约束的元组集建成一个多值决策图,当多值决策图中同构的子图较多时,压缩率较高.在基于STR 的压缩方法中,STR2-C 和STR3-C[12]将多个元组表示为一个c-tuples[13];ShortSTR[14]将多个元组表示为一个短元组;STR-slice[15]将多个元组表示为关联模式的子表;STRbit[16]用和 Compact-Table[17]均采用比特位表示元组序号,一次比特操作可以同时处理多个元组.此类元组集压缩方法维持GAC 的效率受限于压缩率,当压缩率较高时加速显著;当压缩率降低时,加速效果减弱,部分方法会发生退化,例如,MDDc、STR2-C、STR3-C 在压缩率较低的问题上效率低于STR2,STR3.
表约束上的高阶相容性算法[18-21]也受到广泛研究,目前应用较为成功的高阶相容性有pairwise consistency(PWC)[22]以及弱化版PWC,从降低维护代价的角度出发,最新的维持高阶相容性算法,例如FE[8]、FDE[23],均采用对约束问题重构的策略,并证明了采用特定的重构方法,在重构后的问题上维持GAC 等价于对原问题维持PWC 或更高阶段相容性.值得注意的是,这些方法均通过实验证实,使用STR2 对重构后的问题维持GAC 的效率高于MDDc,STR3 在重构问题上维持GAC 的效率.
本文提出的STR2*是一种非基于表压缩的STR 算法,具有直接处理原始表、实现简单等特点.STR2*采用了一种全新的动态维持元组集有效部分的方法,包含效率更高的检测元组有效性以及为变量值更新支持的方法.实验结果表明,STR2*拥有比STR2 和STR3 更高的维持GAC 的效率,在元组集数目极小时,STR2*趋近于STR2;在元组集数目增多时,STR2*相对于STR2 和STR3 提升显著.对于元组集规模缩减较快的问题,STR2*优于现有的基于表压缩的算法.
1 背景知识
一个约束满足问题P=(X,C),其中,X是变量集合{x1,...,xn},C是约束集合{c1,...,ce}.dom(x)是x∈X的当前有效论域.我们使用(x,a)表示x的一个值a(在不引起混淆的情况下,也可直接表示为a),如果a∈dom(x),我们称a是有效的;否则,a是无效的.每个c∈C包括两个部分:scp(c)是X中有序的变量子集,表示c的约束范围,c的元数是|scp(c)|;rel(c)是与scp(c)对应的元组的集合.给定scp(c)={x1,...,xn},rel(c)⊆表示scp(c)包含的变量中所有可满足的值的组合的集合.我们规定,所有元组集都是有序的.给定一个有序变量集合S⊆scp(c)和一个元组t∈rel(c),t关于S的投影t[S]表示t中与S中变量对应的部分.t是(x,a)在c中支持ifft[x]=a.t关于x是有效的 ifft[x]∈dom[x];t是有效的 iff 对于任意x∈scp(c),t关于x是有效的;c关于x∈scp(c)是有效的 iff 对于任意t∈c,t关于x是有效的;c是有效的 iff 对于任意x∈scp(c),c关于x是有效的.显然,c是有效的 iffc中所有元组都是有效的.
定义1(广义弧相容generalized arc consistency(GAC)).对于一个约束满足问题P,(x,a)关于c是GAC 的iffc中存在一个(x,a)的有效支持;x关于c是GAC 的iff 对于任意a∈dom(x),(x,a)关于c是GAC 的;c是GAC 的iff 对于任意x∈scp(c),x关于c是GAC 的;P是GAC 的iff 对于任意c∈C,c是GAC 的.
P的一个解是一个约束范围为X的有效元组,使得所有约束都被满足,P是可满足的iff 存在至少一个解.确定一个约束满足问题是否是可满足的是NP-hard.显然,当一个值(x,a)不是GAC 时,该值不会出现在任何解中,维持GAC 就是通过在回溯搜索的每一个阶段删除所有不满足GAC 的值,产生对搜索树剪枝的效果.
2 STR2*
STR2*基于回溯搜索中动态维持元组集的有效部分的思想,即在搜索的每一阶段变量论域发生删减时,删除所有与被删除的值关联的无效元组;同时,在回溯时恢复因回溯而重新变为有效的元组.STR2*采用如下数据结构.
•table(c)是存储了正表约束c中所有元组的数组,每个元组按在table(c)数组中的位置唯一标识,table(c).length表示约束c中元组的总个数.
•position(c)是存储了约束c中每个元组在table(c)中的位置的数组,c中第i个元组为table(c)[position(c)[i]].在任意时刻,position(c)中的值是{0,1,2,...,table(c).length-1}的排列.
•currentLimit(c)是一个记录position(c)中最后一个有效元组位置的整数,-1≤currentLimit(c)≤position(c).length-1,当currentLimit(c)=-1 时,c中当前有效元组数目为0.
•levelLimit(c)记录回溯搜索中每一次赋值前position(c)中最后一个有效元素的位置,用于对currentLimit(c)的备份和恢复.
table(c)是一个仅用于查询的表,在STR2*中,一个约束c中第n个元组对应变量x位置的取值为a=table(c,x)[t].由于c中元组的个数远大于约束的元数,采用这种表示方法的table(c)可以最大限度地利用连续的存储空间,加速查询速度.position(c)中包含了回溯搜索中c的当前有效元组和无效元组两个部分,其中,position(c)[0]到position(c)[currentLimit(c)]是有效部分,position(c)[currentLimit(c)+1]到position(c)[position(c).length-1]是无效部分.当一个元组position(c)[i]因无效被删除时,我们只需将position(c)[i]与position(c)[currentLimit(c)]交换,然后将currentLimit(c)减1.而回溯时只需恢复currentLimit(c)的值,便实现了对已删元组的恢复.显然,回溯发生后,元组在position(c)中的顺序发生了改变,但这不影响算法的正确性.借助于上述数据结构,STR2*可以动态地维持元组集的有效部分,并且只需要单位时间的恢复代价.STR2*基本沿用了STR2 的数据结构,只是table(c)采用了一种与STR2 中table(c)[5]互补的表示方法.
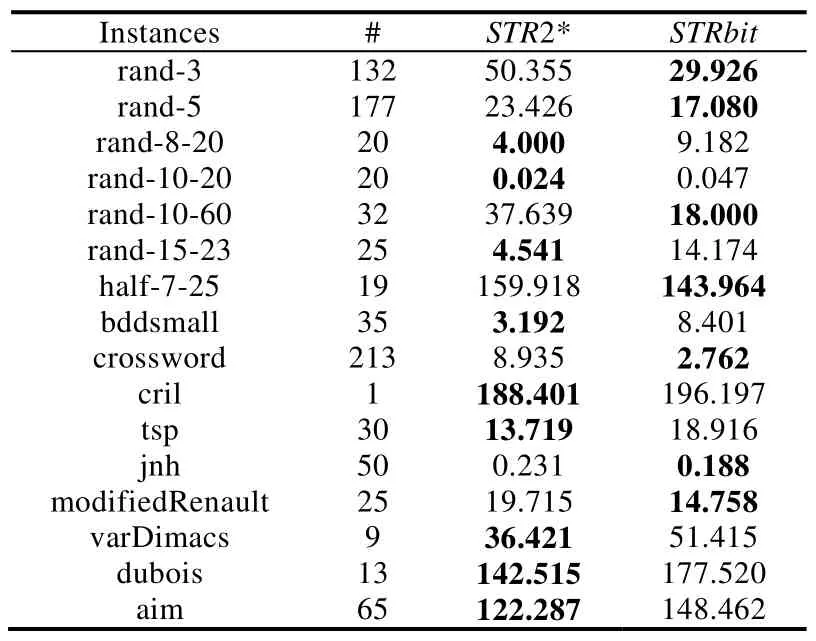
STR2*包含两个部分.第1 部分对应于算法1 的第1 行~第11 行,算法检测约束c中元组有效性并删除无效元组.一个元组是无效的当且仅当存在至少一个(x,a)∈t是无效的.对于任一变量x∈scp(c),如果dom(x)在上次调用STR2*后没有发生改变,则c中所有元组关于x仍然是有效的,无需再次检测.因此,我们仅对c中元组在变量论域发生改变的位置上检测有效性.我们通过变量的时间戳和其所在约束的时间戳大小关系,识别变量论域在上一次调用STR2*后是否发生改变,每一个约束c和每一个变量x在回溯搜索中被赋予一个全局唯一的时间戳.time是一个全局计数器,用于标识不同事件发生的先后次序和更新变量和约束的时间戳,变量x论域发生改变时,stamp[x]被更新为当前的time;在约束c上STR2*时,stamp[c]被更新为当前的time.当stamp[x] 图1 是STR2*在检测阶段动态维持当前有效表的一个例子,scp(c)={x,y,z}. •图1(a)是约束c的table(c),假设初始阶段约束c的状态为currentLimit(c)=10,约束c中满足stamp[x]>stamp[c]的变量集合为{x,y,z},dom(x)={a,b},dom(y)={b},dom(z)={a,c}. •图1(b)是检测c关于x的有效性,即检测position(c)[0]到position(c)[10]中,元组关于x的有效性.8-th~10-th 元组被删除,currentLimit(c)=7. •图1(c)是检测c关于y的有效性,即检测position(c)[0]到position(c)[7]中,元组关于y的有效性.2-th~4-th、7-th 元组被删除,currentLimit(c)=3. •图1(d)是检测c关于z的有效性,即检测position(c)[0]到position(c)[3]中元组关于z的有效性.5-th、0-th元组被删除,currentLimit(c)=3. 最终,c的当前有效元组为6-th、1-th 元组. Fig.1 Demonstration of executing STR2* on the constraint c图1 STR2*在表约束c 上的执行演示 STR2*的第2 部分对应于算法1 的第12 行~第26 行,算法分别为未赋值变量更新支持,并删除没有支持的变量值.外层是对变量的迭代,内层循环是对当前有效元组的迭代.当size=|dom(x)|时,dom(x)中所有值均找到支持,算法跳出当前迭代,对应于算法1 的第21 行、第22 行.所有论域发生删减的变量被更新时间戳,并放入集合Xevt.c中所有变量均被处理后,更新c的时间戳. 算法1.STR2*(c:constraint):set of variables. 算法2.setStamp(m:index of variable or constraint). 性质1.对于包含n个元组的r元约束c,STR2*的时间复杂度为O(r+(Sval+Ssup)×n),其中,Sval表示c中满足stamp[x]>stamp[c]的个数,Ssup表示c中未赋值变量的个数. 证明:算法1 的第2 行和第12 行的时间复杂度为O(r),检测元组集关于一个变量有效性的复杂度为O(n),因此,第1 部分的时间复杂度为O(r+Sval×n).在剩余的有效元组集上,为一个变量查找支持的复杂度为O(n),因此,第2 部分的时间复杂度为O(r+Ssup×n).STR2*的总时间复杂度为O(r+(Sval+Ssup)×n).□ 我们在非二元正表约束上测试STR2*与现有STR 算法的性能.测试所用实例均来自CSP 求解大赛,可在http://www.cril.univ-artois.fr/~lecoutre/#下载.我们测试了正表实例,并将部分包含负表的实例转换成正表测试.程序采用java 编写,运行环境为Intel i5@3.2Ghz 处理器、4GB 内存、windows10 64 位操作系统.回溯搜索采用dom/ddeg的变量启发式、字典序的值启发式和domv的revise启发式[24].每个实例的求解时间上限为600s,T/O表示求解时间超过600s,所有算法均在找到第1 组解或判定无解后结束. 表1 分别给出了STR2*、STR2 和STR3 在多组实例集上的平均运行结果.#表示每组实例集测试的实例的个数;STR2*、STR2 和STR3 分别表示3 种算法的平均运行时间,单位是s;avgTuple是回溯搜索中表约束的平均大小;avgP是avgTuple与初始表约束大小的比值;avgSval是回溯搜索中Sval的平均大小.在图2 的散点图中,每个点表示一个实例. Table 1 Mean results of different algorithms表1 不同算法的平均结果 Fig.2 Comparisons of STR2 and STR2*,STR3 and STR2* in duration for finding a solution图2 STR2 和STR2*、STR3 和STR2*的求解时长的对比 •STR2* VS STR2 STR2*采用全新的动态维持元组集有效部分的方法维持GAC 的效率显著高于STR2.当avgTuple>>avgSval时,STR2*相对于STR2 拥有4 倍以上的效率提升.对于一些表约束规模极小的实例,avgTuple近似等于avgSval,STR2 和STR2*维持元组集有效部分的代价都很低,两种算法的效率近似.表1 和图2 中左图可以看出,STR2*整体优于STR2,在大多数实例上有2 倍~4 倍的效率提升. •STR2* VS STR3 在一些表约束规模极小的问题上,STR2*得益于运用的数据结构简单维护代价较低,求解效率高于STR3.在多数实例上,随着搜索的向下进行,元组集规模缩减较快,avgP<30%,STR2*优于STR3;在少数元组集缩减较慢的实例上,avgP>30%,并且表约束规模足够大时,STR3 优于STR2*.从表1 和图2 中右图可以看出,在绝大多数实例上,STR2*优于STR3;在部分实例上,STR2*的效率是STR3 的20 倍以上. 我们同样将STR2*与基于表压缩的STR 算法进行了对比,基于表压缩的STR 采用分目前公认性能最优的STRbit.表2 中,STR2*和STRbit分别表示3 种算法的平均运行时间,单位是s.图3 是STR2*和STRbit 效率对比的散点图,每个点代表一个问题实例. Table 2 Mean results of STR2* and STRbit表2 STR2*和STRbit 的平均结果 Fig.3 Comparisons of STRbit and STR2* in duration for finding a solution图3 STRbit 和STR2*的求解时长的对比 •STR2* VS STRbit 在一些拓扑结构复杂且表约束规模较小的实例上,例如aim、varDimacs 和dubois,两种算法维持元组集有效部分的代价都比较低,STR2*得益于运用的数据结构简单维护代价较低,求解效率稍优于STRbit.在一些元组集规模缩减较快的实例上,例如rand-15-23、rand-8-20 和bddsmall,STR2*优于STRbit,拥有超过2 倍的效率提升.表2 可以看出,STR2*在所有16 类问题的9 类中优于STRbit.由于不同类问题的实例集中的实例个数差别较大,例如STRbit 效率更高的rand-3、rand-5 和crossword 这3 类问题的实例总个数占到所有测试实例的60%,在图3 的散点图中,才会有STRbit 在多数实例上效率优于STR2*的效果. 我们提出了一种表约束上维持GAC 的算法STR2*,采用了一种新的动态维持元组集有效部分的方法.实验结果证实,STR2*维持GAC 的效率均高于STR2 和STR3,并且在元组集缩减较快的问题以及元组集规模较小的问题上优于最新的采用表压缩的STRbit.今后,我们希望将这种新的动态维持元组集有效部分的方法运用到其他基于STR 的算法中.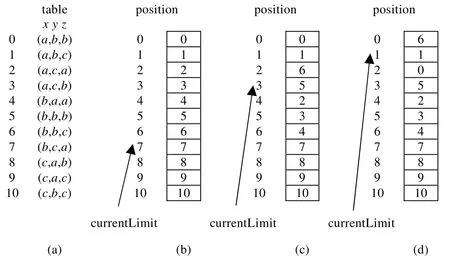


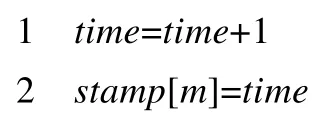
2.1 复杂度分析
3 实验结果及分析



4 总结

