高精度压力机连杆机构的误差分析及精度综合

骞华楠， 陶 璟， 于随然

(上海交通大学 机械与动力工程学院， 上海 200240)

近净成形技术可以使生产的零件接近或者达到最终所需的形状和尺寸[1]，是一种高效、节能的先进制造技术[2].相比发达国家，我国近净成形技术发展水平仍处于起步探索阶段，在整个成形制造生产中所占比重还比较低，其关键困难之一在于我国还缺少近净成形配套的高精度设备.多连杆伺服压力机兼有伺服运动柔性可控和现代并联机构的精度高、承载能力强的优点[3]，因此是高精度压力机发展的主要趋势.Guo[4]、He[5]、Huang[6]等人基于冗余驱动方式对新型并联驱动压力机的构型进行了研究，促进了我国多连杆压力机的开发.精度设计是保障压力机精度的重要环节，然而传统压力机的精度设计中各零部件精度参数的确定大多依赖于设计人员的经验，难以兼顾成本需求，因此开展压力机连杆机构误差分析和精度综合的研究对高精度压力机的设计开发至关重要.

为研究机构各误差源与整体输出精度间的关系，相关学者提出了多种误差建模方法[7].莫志翔等[8]基于直接线性化的方法构建了手术机器人运动中心的误差模型，通过分析各误差因素敏感度确定了影响其定位精度的关键因素.Chaker等[9]以5种不同的非过约束球面并联机构(SPM)为研究对象，分析了连杆制造误差对其输出末端平台位姿的影响，结果表明不同类型的SPM具有不同的位姿精度.白勇军[10]对压力机的典型多连杆机构进行了误差分析，研究了原动件输入误差、杆件长度误差以及安装位置误差等对运动输出的影响，但对于机构对称性假设过于简单，未能充分考虑结构误差存在的多种情况，因此不能准确地反映误差对运动输出的影响.

机构的精度综合是误差分析的逆问题，是指在预定整体精度的要求下优化分配其各组成部件的公差，因而更具有工程实际意义.余治民等[11]基于响应面法建立了大型龙门导轨磨床的加工精度可靠性近似模型，以可靠度的均值和最小值为目标，按照精度均衡原则对磨床主要部件的精度进行了优化.Li等[12]为提高空间并联机构位姿精度，基于实验设计的方法对其进行了公差综合，降低了制造和装配的难度.从现有相关研究来看，由于相对缺乏伺服压力机多连杆精度综合的研究，难以兼顾制造成本等因素的影响.

1 并联多连杆压力机误差建模

1.1 研究对象

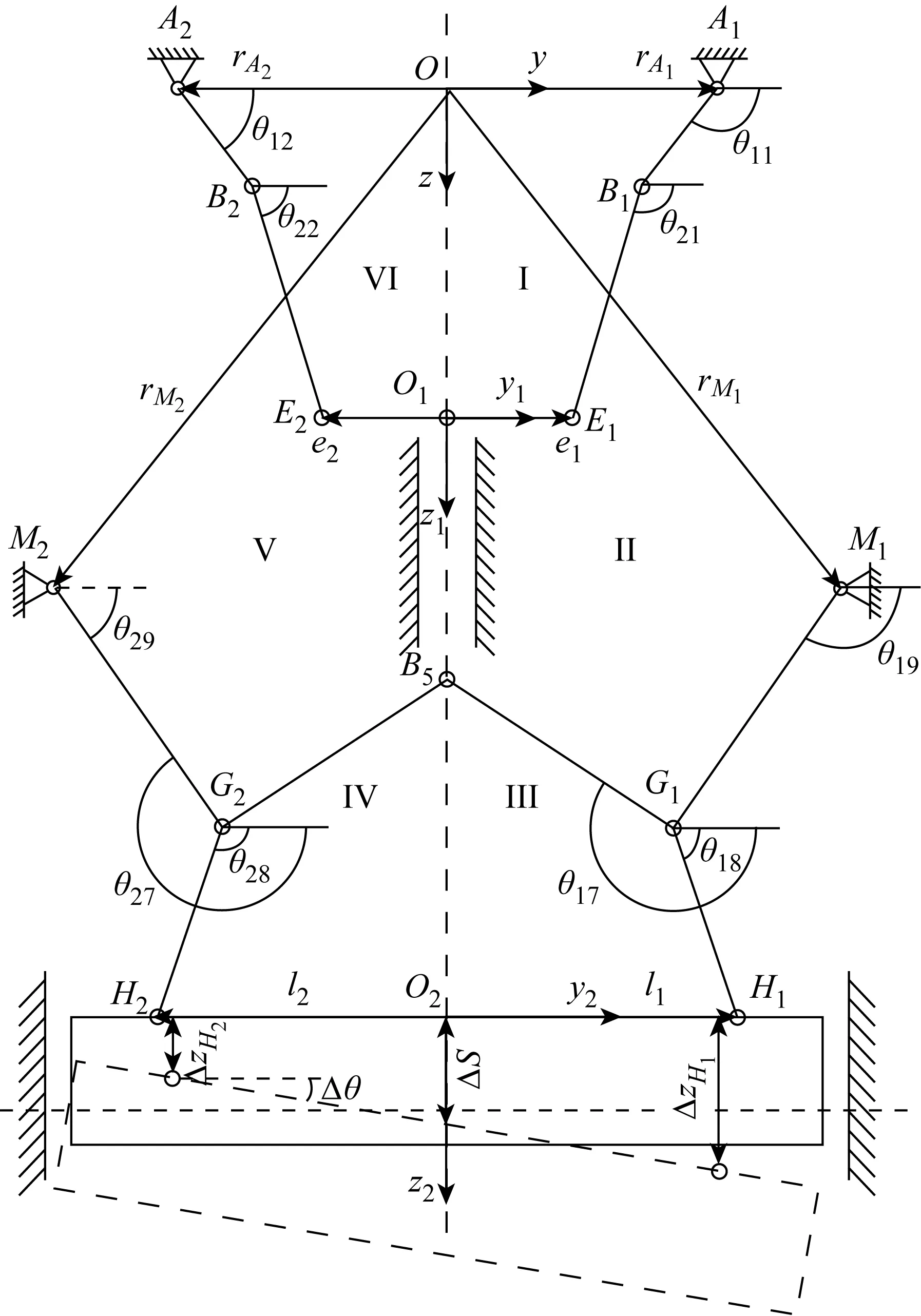
图1 简化后的并联多连杆压力机的机构简图Fig.1 Schematic of simplified parallel driven multi-linkage press mechanism

1.1.2机构构型简化 根据机构构型的特点，做以下简化：① 假设传动系统主动支链中的结构误差不影响滑块倾角，而仅仅影响滑块位置误差；② 假设整个传动系统前后部分对应的误差相同，仅考虑y轴和z轴方向的误差，从而将空间机构简化为平面机构进行分析.

1.2 并联多连杆压力机精度影响因素

滑块的运动精度集中反映了压力机的精度水平，是评价压力机精度主要的性能指标.综合柳乔[13]、牛瑞霞[14]等人的研究，本文中滑块运动精度是指当主动件的位置一致时，滑块输出位置、角度的实际值与理论值间的符合程度，并采用滑块运动输出位置误差ΔS和输出角度误差Δθ两个指标进行表征.

影响机构运动输出误差的因素包括连杆机构本身固有的结构、有限的制造精度、安装的误差、运动副间隙、构件承受载荷后的弹性变形、摩擦磨损、振动以及温度等[7].根据研究对象的特点，并参考相关的研究[10,15]，本文主要分析原动件输入、杆件长度以及各构件安装位置的误差对滑块运动输出误差的影响.

1.3 基于环路增量法的并联多连杆压力机误差建模

如图1所示，将传动系统分为6个环路，即环路I—OO1E1B1A1O、环路 II—OO1B5G1M1O、环路 III—OO2H1G1M1O、环路 IV—OO2H2G2M2O、环路 V—OO1B5G2M2O以及环路 VI—OO1E2B2A2O.已知压力机的结构参数以及相应的误差项如表1和2所示.

表1压力机传动连杆参数及相应的误差项

Tab.1Transmissionlinkparametersandcorrespondingerrorsofservopress

构件杆长与y轴夹角杆长误差A1B1,A2B2a1,a2θ11,θ12δa1,δa1B1E1,B2E2kR1,kR2θ21,θ22δkR1,δkR2O1B5kπ/2δkB5G1,B5G2lg1,lg2θ17,θ27δlg1,δlg2M1G1,M2G2lm1,lm2θ19,θ29δlm1,δlm2G1H1,G2H2lh1,lh2θ18,θ28δlh1,δlh2

表2压力机安装位置参数及相应的误差项

Tab.2Installationlocationparametersandcorrespondingerrorsofservopress

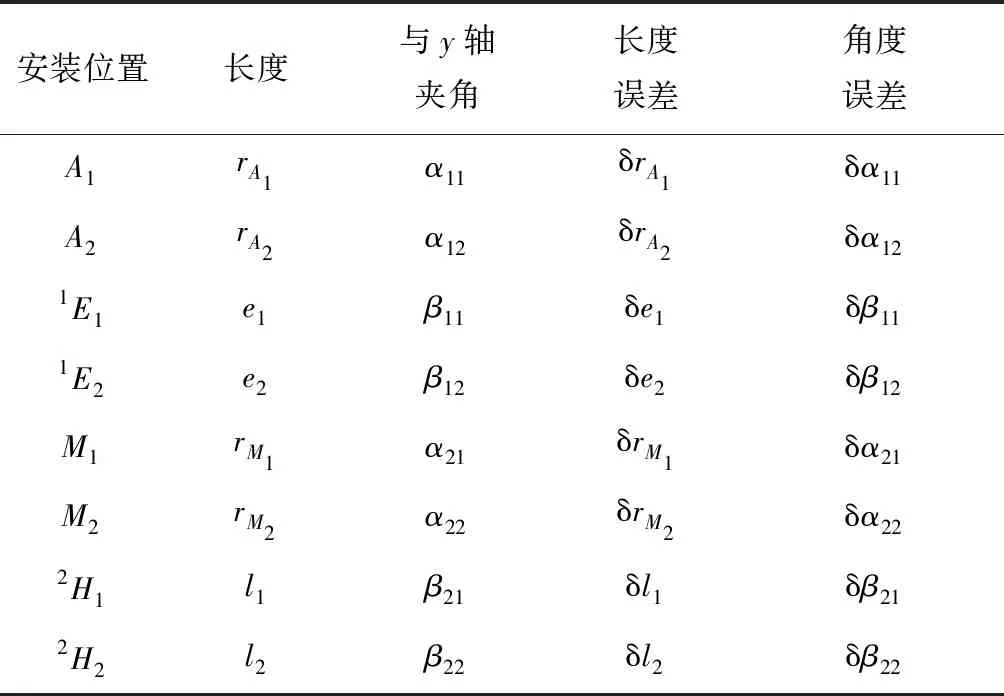
安装位置长度与y轴夹角长度误差角度误差A1rA1α11δrA1δα11A2rA2α12δrA2δα121E1e1β11δe1δβ111E2e2β12δe2δβ12M1rM1α21δrM1δα21M2rM2α22δrM2δα222H1l1β21δl1δβ212H2l2β22δl2δβ22

由图1可得环路 I、II、III、IV、V、VI 的闭环矢量方程为

(1)

以环路Ⅰ为例说明，由闭环矢量方程可得复数形式的运动方程为

z1ej90+e1ejβ11=rA1ejα11+a1ejθ11+kR1ejθ21

(2)

式中：z1为动平台输出位置.

对式(2)求一次导数，将微分形式写为增量形式，并将等式两边同乘以e-jθ，可得单回路机构的位置误差增量方程为

Δz1ej(90-θ)+δe1ej(β11-θ)+δβ11e1ej(β11-θ)j=

δα11rA1ej(α11-θ)j+δrA1ej(α11-θ)+δa1ej(θ11-θ)+

δθ11a1ej(θ11-θ)j+δkR1ej(θ21-θ)+δθ21kR1ej(θ21-θ)j

(3)

令θ=θ21以消去变量δθ11，并对等式两端取实部可得动平台输出误差Δz1为

Δz1=[-δe1cos(β11-θ21)+δβ11e1sin(β11-θ21)+

δrA1cos(α11-θ21)-δα11rA1sin(α11-θ21)+

δa1cos(θ11-θ21)-δθ11a1sin(θ11-θ21)+

(4)

对环路 II、III、IV、V、VI 进行同样的分析，通过令θ为不同的值来消去变量，从而得到各杆件的输出角度误差Δθ17、Δθ27、Δθ18、Δθ19、Δθ28、Δθ29，进而得到滑块运动输出误差ΔzH1、ΔzH2分别为

ΔzH1=δrM1sinα21+rM1δα21cosα21+

δlm1sinθ19+Δθ19lm1cosθ19+δlh1sinθ18+

Δθ18lh1cosθ18+l1δβ21

(5)

ΔzH2=δrM2sinα22+rM2δα22cosα22+

δlm2sinθ29+Δθ29lm2cosθ29+δlh2sinθ28+

Δθ28lh2cosθ28+l2δβ22

(6)

由误差独立作用原理可知，压力机传动系统各误差因素对机构输出的影响相互独立，所以传动连杆与滑块的连点输出误差等于各误差引起的局部输出误差之和.对于对称机构而言，由于各构件原始误差的积累，使得连杆与滑块连点的输出误差存在以下3种情况：

(1) 当ΔzH1=ΔzH2≠0时，只对运动输出位置误差ΔS有影响，对运动输出角度误差Δθ无影响;

(2) 当ΔzH1=-ΔzH2时，只对运动输出的角度误差Δθ有影响，对输出的位置误差ΔS无影响;

(3) 当|ΔzH1|≠|ΔzH2|时，对输出的位置误差ΔS和角度误差Δθ都有影响.

为全面考虑实际误差存在的情况，由误差ΔzH1、ΔzH2可得滑块输出位置误差、角度误差表达式分别为

2 基于灵敏度分析的关键结构误差识别

2.1 各误差因素的灵敏度和显著度

采用误差灵敏度来反映各个误差因素的微小变化对总输出误差的影响情况.误差灵敏度为滑块运动输出误差对各个误差因素偏导数的绝对值.若第m项误差Δm的灵敏度为ξm，则有

(9)

m=1,2,…,n

式中，Eout为滑块输出误差；n为误差因素的个数.

为确定影响机构运动输出的显著误差因素，采用显著度指标来表征滑块在不同位置时受各项误差因素的影响程度.显著度数值越大表明其所对应的误差项对机构末端输出误差的影响越显著.当滑块处于某一位置时，第m项误差的显著度Dm为

(10)

2.2 MATLAB仿真和结果

给定压力机的结构参数如下：a1=a2=0.36 m，kR1=kR2=1.304 m，k=0.6 m，l1=l2=1.6 m，lm1=lm2=1.7 m，lg1=lg2=0.868 m，lh1=lh2=1.6 m，rA1=rA2=1.2 m，e1=e2=0.3 m，rM1=rM2=1.393 m；α11=0，α12=π rad，β11=0，β12=π rad，α21=0.117 rad，α22=3.023 rad，β21=0，β22=π rad[10].借助MATLAB仿真软件可计算出各误差因素对滑块输出误差影响的灵敏度，进而求取各个误差因素的显著度.滑块下死点位置处的输出精度是影响压力机成形质量的关键因素，故本文分析在该位置时各误差因素的影响情况.

2.2.1各参数对滑块输出位置误差的影响 图2所示为传动系统主动支链和被动支链的各结构参数误差对滑块输出位置误差影响的显著度.由图2可知，在下死点位置时，对滑块输出位置误差影响较大的关键误差源有12项，即点H、M的安装位置误差δl1(2)(δl1(2)表示δl1(δl2)，下同)、δβ21(22)、δα11(12)及杆件MG、B5G、GH的制造误差δlm1(2)、δlg1(2)、δlh1(2).这12项误差的显著度之和为 0.876 6，在压力机制造和安装时，要注意限定其误差值.

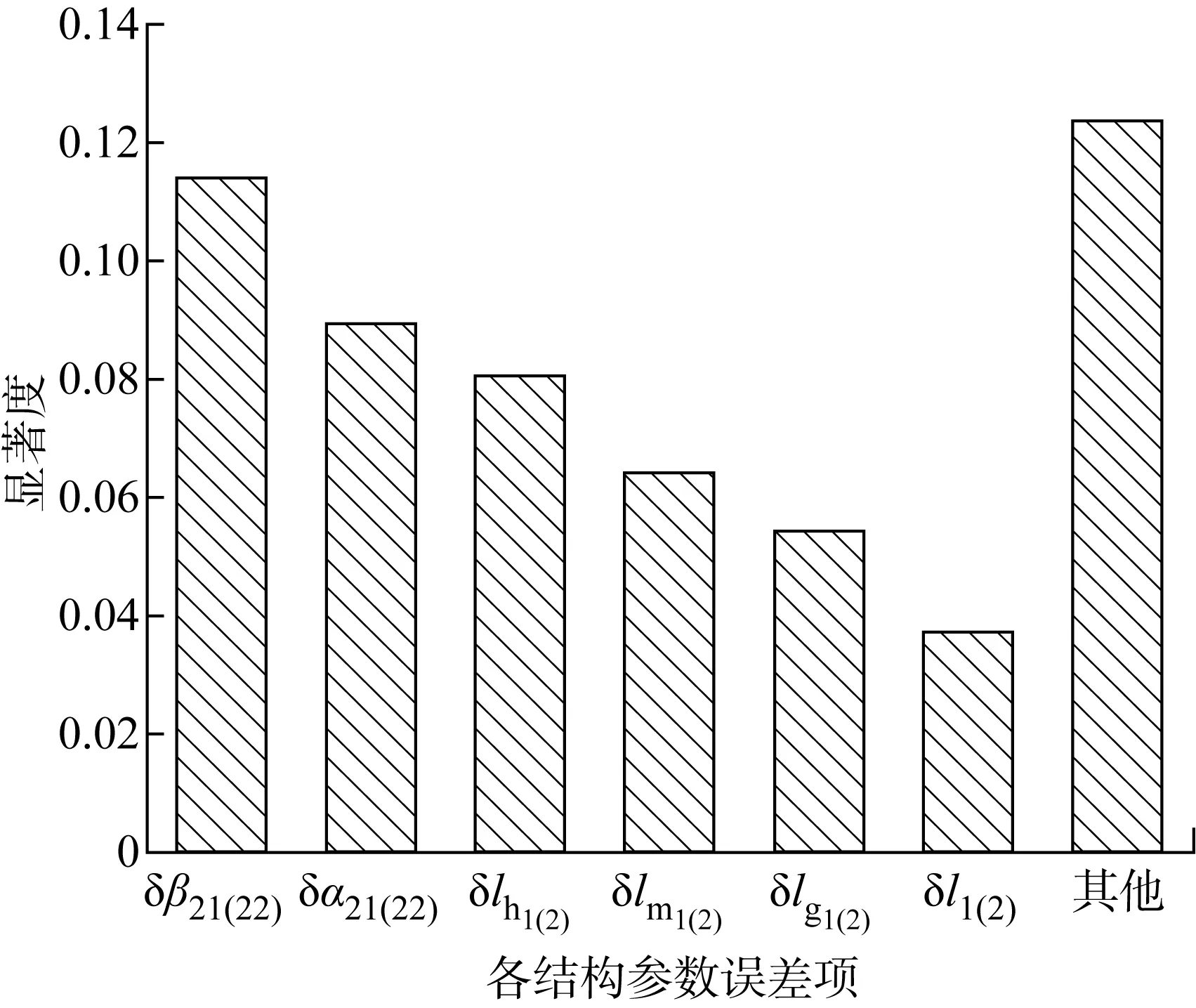
图2 关键结构参数误差对滑块输出位置误差影响的显著度Fig.2 The salience of key errors to output position of the slider

2.2.2各参数对滑块输出角度误差的影响 图3所示为传动系统被动支链的各结构参数误差对滑块输出角度误差影响的显著度.由图3可知，在下死点位置时，对滑块输出角度误差影响的关键误差源有10项，即点H、M的安装位置误差δβ21(22)、δα11(12)及杆件MG、B5G、GH的制造误差δlm1(2)、δlg1(2)、δlh1(2).这10项误差的显著度之和为 0.900 6，是影响滑块输出角度误差的主要因素.

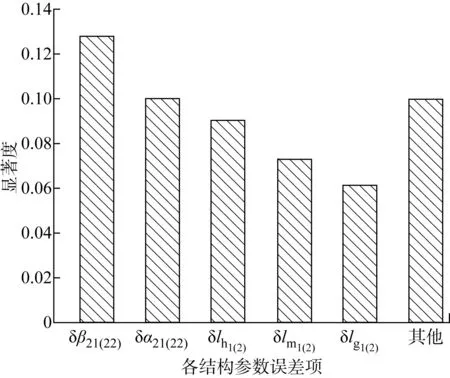
图3 关键结构参数误差对滑块输出角度误差影响的显著度Fig.3 The salience of key errors to output angle of the slider

3 关键部件精度综合

对压力机而言，滑块下死点位置处的精度是影响工件成形质量的主要因素，因此本文将在滑块处于下死点位置时对机构进行精度综合.以提高滑块输出可靠度为目标，综合考虑各误差的灵敏度以及误差控制成本的影响，提出了适用于并联压力机连杆系的精度综合方法，其流程如图4所示.

图4 并联多连杆压力机精度综合流程图Fig.4 Flow chart of accuracy synthesis for parallel driven multi-linkage press

3.1 基于经验初步确定各部件的公差值

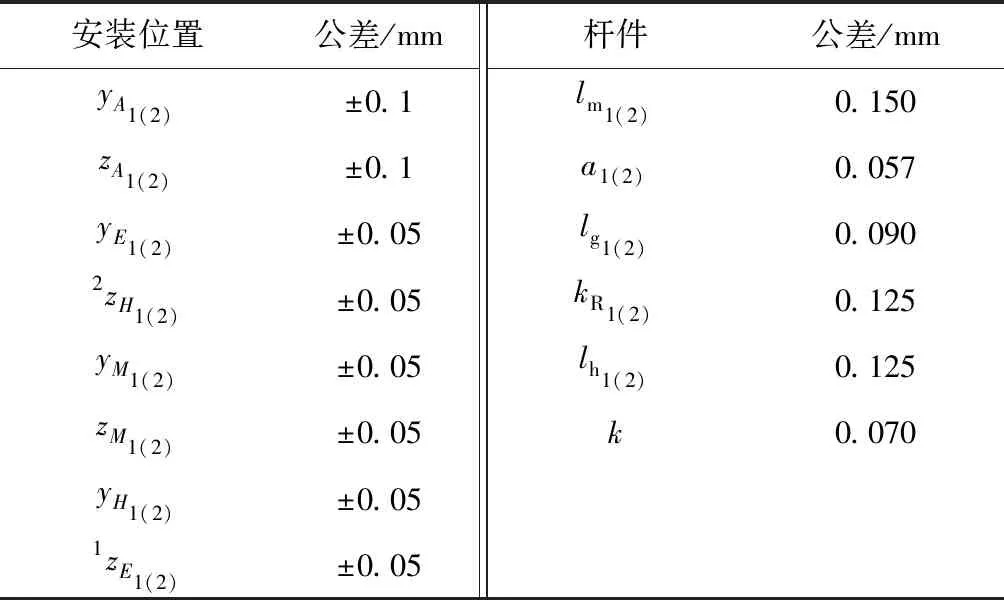
在公差调整前，对压力机传动机构的安装位置误差按照经验进行取值，结果如表3所示.对各杆件的公差，考虑到各加工方法的经济加工精度，初步选择其公差等级为7级，相应的公差值见表3.

表3压力机传动系统安装位置及杆件公差

Tab.3Installationlocationandtransmissionlinkparameterstolerancesofservopress

安装位置公差/mm杆件公差/mmyA1(2)±0.1lm1(2)0.150zA1(2)±0.1a1(2)0.057yE1(2)±0.05lg1(2)0.0902zH1(2)±0.05kR1(2)0.125yM1(2)±0.05lh1(2)0.125zM1(2)±0.05k0.070yH1(2)±0.051zE1(2)±0.05

3.2 滑块输出精度可靠性分析

现代机械精度设计理论表明，零部件的制造误差为随机量，当大批量生产时，其满足正态分布.基于误差独立作用原理以及随机变量方差的计算规则，可知滑块输出位置误差、角度误差的均方差为

(11)

(12)

式中:ξi、ξj分别为影响滑块输出位置误差、角度误差的各因素灵敏度；σi、σj分别为影响滑块输出位置误差、角度误差的各因素均方差.

滑块输出误差的可靠度是指其运动输出落在压力机允许最大误差范围内的概率.为满足精密级压力机的设计要求，本文设定滑块输出位置误差ΔS小于 0.02 mm的可靠度不低于88%，而角度误差Δθ小于 0.001 3 rad的可靠度不低于95%.基于概率统计原理，并运用MATLAB软件编写计算程序，可求得初始公差方案下的可靠度为

由上述滑块输出误差的可靠度可知，初始公差方案不满足设计要求，需要对其进行调整.

3.3 公差调整时各个因素顺序的确定

在对影响机构输出精度的各因素公差进行调整时，往往仅考虑了灵敏度分析的结果，而忽略了加工成本的影响，为此在综合考虑以上两方面影响因素的基础上确定各杆件的调整顺序.

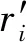
(13)

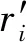
(14)

(15)

考虑滑块输出精度和构件制造成本同等重要，故取权重系数P1=P2=1，则各构件的综合系数如表4所示，较小的ri所对应的因素要优先进行调整.

表4考虑加工成本和灵敏度的各构件综合系数

Tab.4Eachcomponent’scoefficientconsideringprocessingcostsandsensitivity

构件综合系数构件综合系数lg1(2)1.426kR1(2)4.281a1(2)4.876lh1(2)1lm1(2)1.040k5.389

3.4 基于精度均衡原则的关键部件精度综合

由上述分析可知各因素调整顺序为lh1(2)、lm1(2)、lg1(2)、kR1(2)、a1(2)、k，在对压力机各部件的公差进行调整时遵循精度均衡原则，优先调整没有调整过的因素.每次调整的因素、调整量以及调整后的可靠度如表5所示.

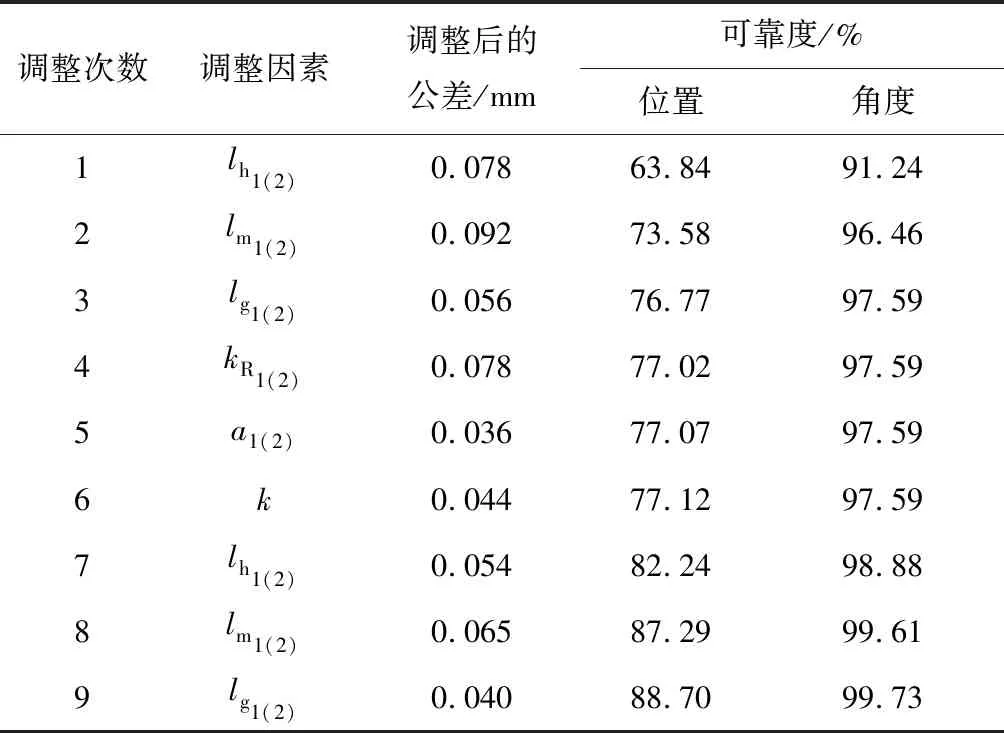
表5 调整因素和调整后的可靠度Tab.5 Adjustment factors and adjusted reliability

3.5 基于Monte Carlo法的可靠度分析

基于零部件制造误差满足正态分布的假设，按照3σ原则取公差带宽的1/6为标准差来进行抽样[12].将抽样产生的随机数代入式(7)和(8)，通过Monte Carlo仿真104次可得到其均方差，进而能够计算出相应的可靠度，如表6所示.由表6可知，采用Monte Carlo法计算得到的滑块位置误差可靠度、角度误差可靠度与理论计算的结果一致，验证了本文所提出方法的有效性.

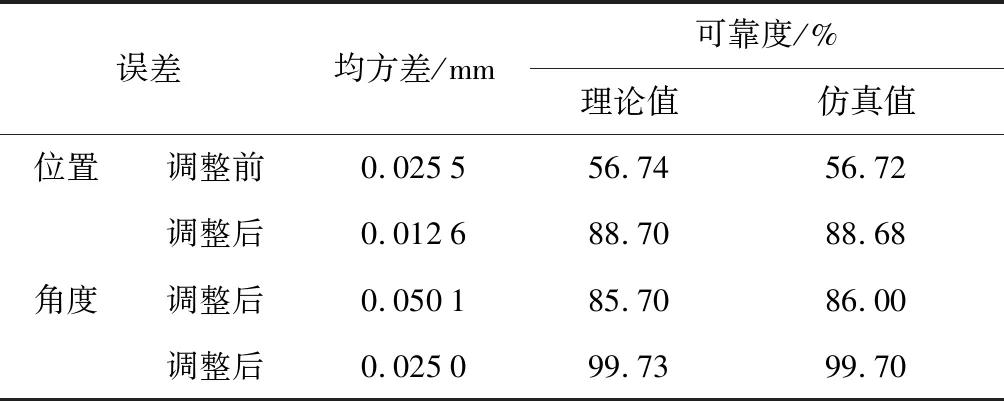
表6 滑块输出误差的可靠度Tab.6 Reliability of slider output error

经过9次调整后，滑块输出位置误差的可靠度由 56.74% 升至 88.70%，滑块输出角度误差的可靠度由 85.70% 升至 99.73%，均满足了设计要求，从而最终确定了压力机关键部件的合理公差.

4 结论

(1) 针对并联多连杆伺服压力机连杆机构结构特性，分析了机构误差类型，提出了基于环路增量法的滑块输出位置误差和角度误差解析模型.通过灵敏度分析，量化了各误差项对滑块关键位置精度的影响程度.以提高滑块输出精度可靠度为目标，综合考虑各误差灵敏度及误差控制成本，提出了适用于并联压力机传动连杆的精度综合方法.