屏蔽式核主泵飞轮裂纹寿命评估

刘昺轶， 张继革， 王德忠， 李 斌

(上海交通大学 核科学与工程学院， 上海 200240)

屏蔽式核主泵飞轮的主要功能是保证主泵在发生断电事故后仍然可以提供一定的惰转流量，将堆芯残余热量带走，是保障反应堆安全运行的重要部件.其结构为双金属飞轮，几何模型较为复杂，在运行时承受装配应力、离心力以及高温载荷引起的热应力的综合影响.在高转速下，飞轮破碎可能对一回路压力边界形成冲击.

美国EMD公司曾制造双金属飞轮模拟件，通过超速旋转实验测试其性能后发现保持环上有一处裂纹[1]，经研究认为该裂纹是在装配和加工过程中产生的.飞轮在启停过程中承受交变应力的作用，其表面的初始裂纹深度随着循环周期的增加而不断增长直至临界值，最终导致飞轮发生断裂失效，从而影响核主泵寿期内的安全运行，所以有必要对飞轮裂纹进行寿命评估.

近年来国内外学者对飞轮裂纹应力强度因子的计算方法以及其寿命的评估开展了一系列相关工作. Park等[2]建立了存在裂纹的三维飞轮模型，利用裂纹上下部的位移差计算其应力强度因子，并使用Paris公式评估其寿命，但忽略了应力强度因子随裂纹深度增加而产生的变化，导致其结果并不保守.在EMD公司出具的双金属飞轮完整性计算报告中只对飞轮材料的断裂韧性及假想裂纹尺寸提出了要求[3]，并无相关分析.文献[4-5]中参考ASME附录G[6]对飞轮裂纹的应力强度因子进行计算，但ASME附录G只适用于诸如压力容器、管道、泵体等承压部件，并且双金属飞轮保持环所使用的材料也超出了其经验系数的适用范围.文献[7-8]中将飞轮简化为半无限大体，使用半经验公式对飞轮裂纹进行应力强度因子的计算及寿命评估，虽然取得了一定的成果，但仍有待深入研究.综上所述，现有的研究方法并不适用于结构、受力复杂的双金属飞轮.

本文以屏蔽式核主泵飞轮为研究对象，建立了存在裂纹的飞轮实际模型，开展了关于飞轮裂纹应力强度因子变化规律的研究，对核主泵寿期内的安全运行而言具有重要意义.

1 计算模型及边界条件

屏蔽式核主泵的结构示意图如图1所示，飞轮的结构及计算模型如图2所示.内轮毂、钨合金块和保持环的材料分别为重钨合金(钨质量分数为97%)、403不锈钢和马氏体时效钢，飞轮材料的力学性能如表1所示.

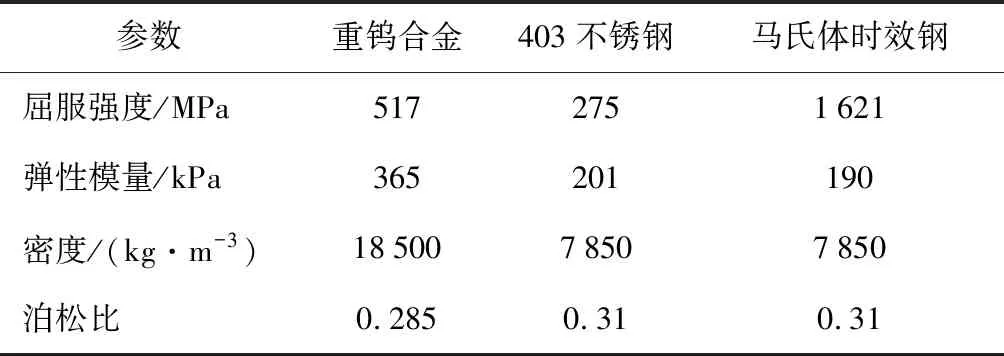
表1 飞轮材料力学性能Tab.1 Mechanical property of flywheel

飞轮为循环对称结构，故采用1/12模型进行计算.因为重钨合金的密度大于马氏体时效钢，钨合金块对称放置，所以即使在高转速工况下，保持环与钨合金块以及钨合金块与钨合金块之间也不会发生相对滑动，又因为钨合金与钨合金及钨合金与钢之间的摩擦系数为 0.2～0.6，所以本文采取了相对保守的设置，即采取摩擦接触设置，摩擦系数取 0.2.

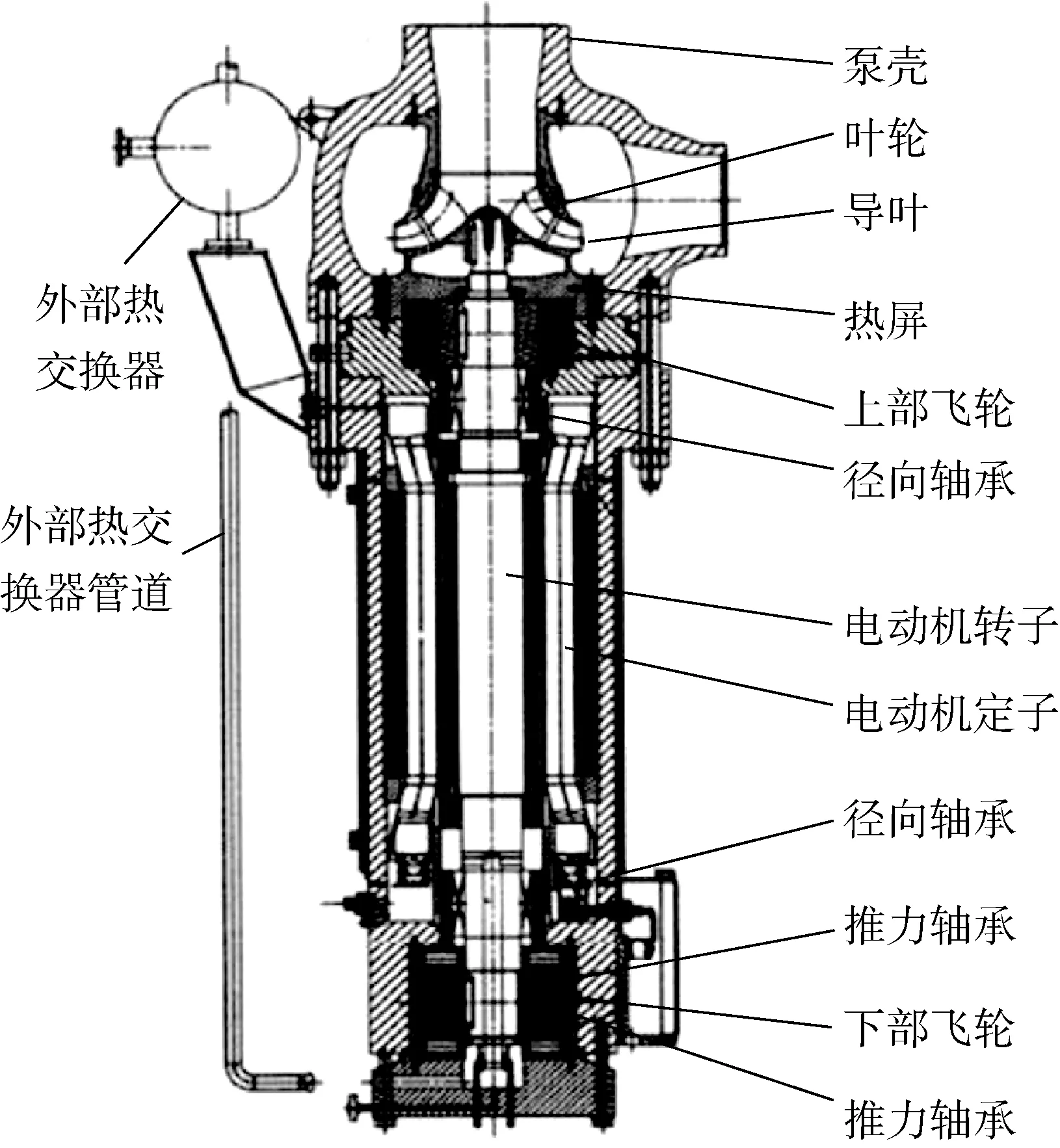
图1 屏蔽式核主泵结构示意图Fig.1 Structure diagram of canned main pump

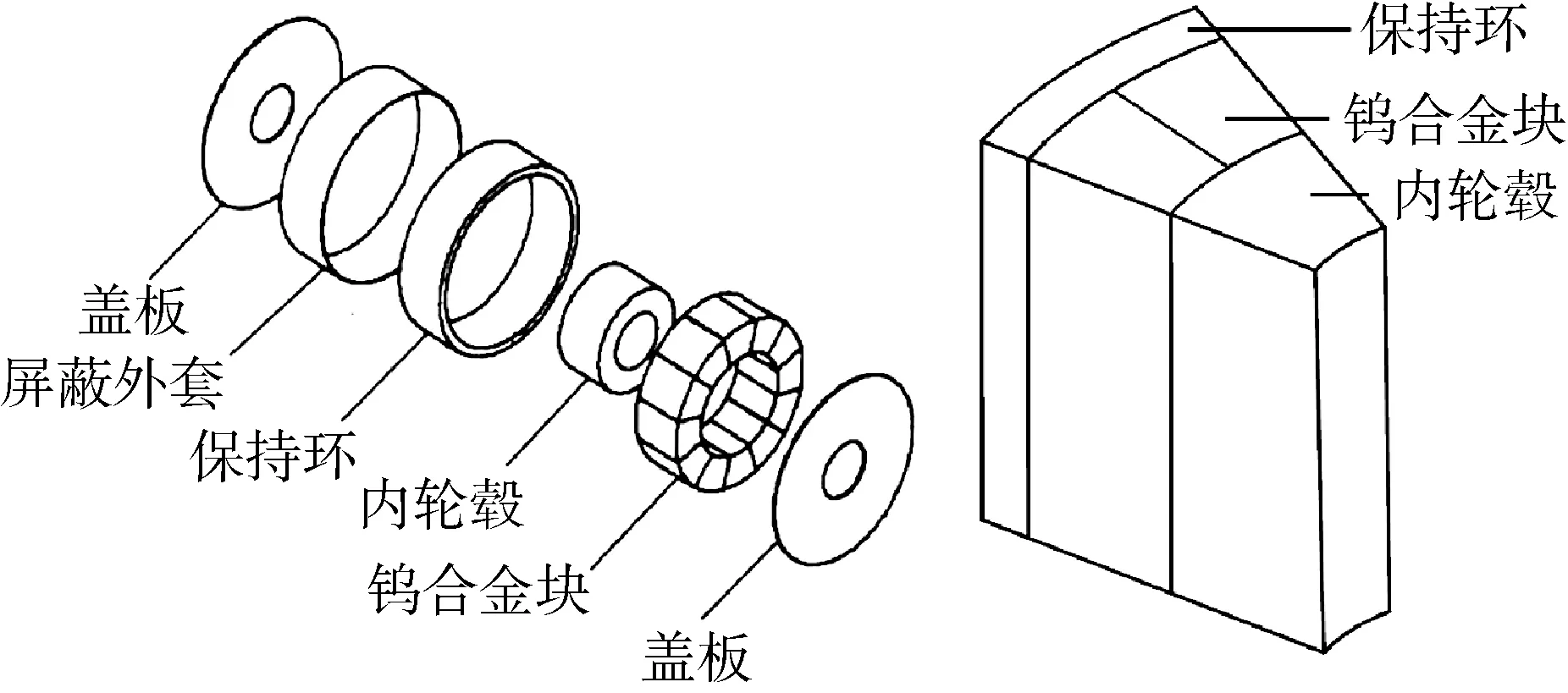
图2 飞轮结构及计算模型Fig.2 Structure and calculation model of flywheel

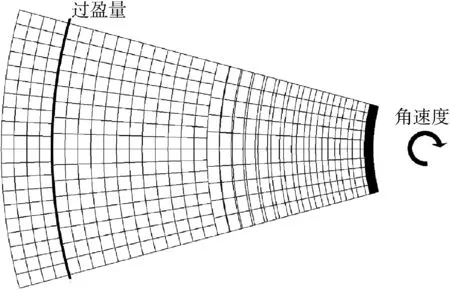
图3 飞轮网格及边界条件Fig.3 Mesh of flywheel and boundary conditions

网格划分方案共10种，网格数为150～45 000，经无关性检验后，最终确定模型网格数为 13 798，如图3所示.计算时综合考虑热应力、装配应力以及离心力的影响，在模型两侧设置无摩擦约束(Frictionless Support)，通过Workbench中的多物理场耦合功能(Import Load)将CFX中计算得到的温度场加载至飞轮整体，在钨合金块与保持环之间通过Connection中的Offset选项设置过盈量，最后利用Rotational Velocity功能对飞轮整体施加各工况下的角速度.

2 应力强度因子计算

结合EMD公司出具的双金属飞轮完整性计算报告[3]及初步的结构强度计算可知，其保持环内表面与钨合金块的接触位置应力较大，为了考虑最危险工况，在该处引入假想裂纹.在力学分析中，表面的裂纹的形状常常用半椭圆来描述[9]，其尺寸及形状参照NUREG-0800[10]以及EMD计算报告，裂纹深度为 6.35 mm (0.25 in)，裂纹长度为 20.2 mm (0.795 in)，该裂纹尺寸综合考虑了飞轮在役期间由于力学性能退化引起的扩展，以及超声波所能检测到的最小裂纹尺寸.裂纹的具体位置及网格划分如图4所示.

马氏体时效钢为高强度钢，故采用线弹性断裂力学模型结合K准则计算其应力强度因子.在设计转速工况下，飞轮裂纹处的应力分布(轴向截面视图)如图5所示.

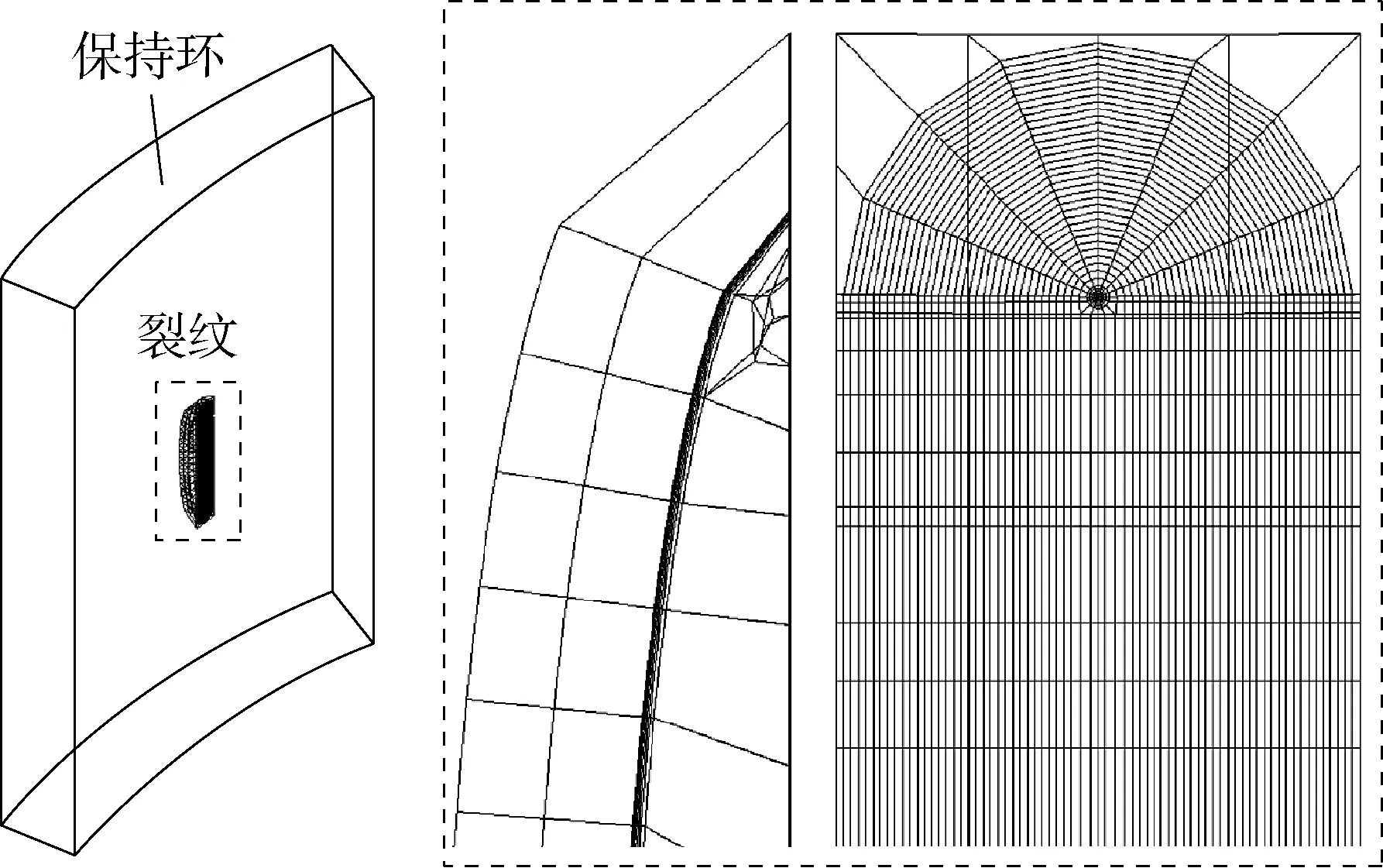
图4 裂纹位置及网格Fig.4 Location and mesh of crack

图5 裂纹处应力分布Fig.5 Stress distribution of crack

由于引入了假想裂纹，飞轮在结构上出现了几何不连续，裂纹前缘以及保持环内表面开裂处存在明显的应力集中.此时基于连续介质理论的弹塑性分析已然失效，所以裂纹周围依照弹塑性模型计算的得到应力大小仅有参考意义，并非后续计算裂纹应力强度因子的输入.

在后处理中插入Fracture Tool模块对裂纹进行绕线积分以提取其应力强度因子，飞轮裂纹的应力强度因子如图6所示.

图6 裂纹处应力强度因子Fig.6 Stress intensity factor of crack

NUREG-0800[10]明确规定，飞轮所用材料的断裂韧性应不小于165 MPa·m1/2，故裂纹处的最大应力强度因子应小于该值.此时裂纹的应力强度因子最大值出现在裂纹前缘的中间位置，其值为106 MPa·m1/2(即 3 338 MPa·mm1/2)，小于165 MPa·m1/2，所以保持环不会发生断裂.

2.1 应力强度因子与飞轮转速的关系

为了揭示飞轮裂纹的应力强度因子随转速、裂纹深度及长度的变化规律，本文采用控制变量法进行研究，其中应力强度因子随转速的变化规律如图7所示.

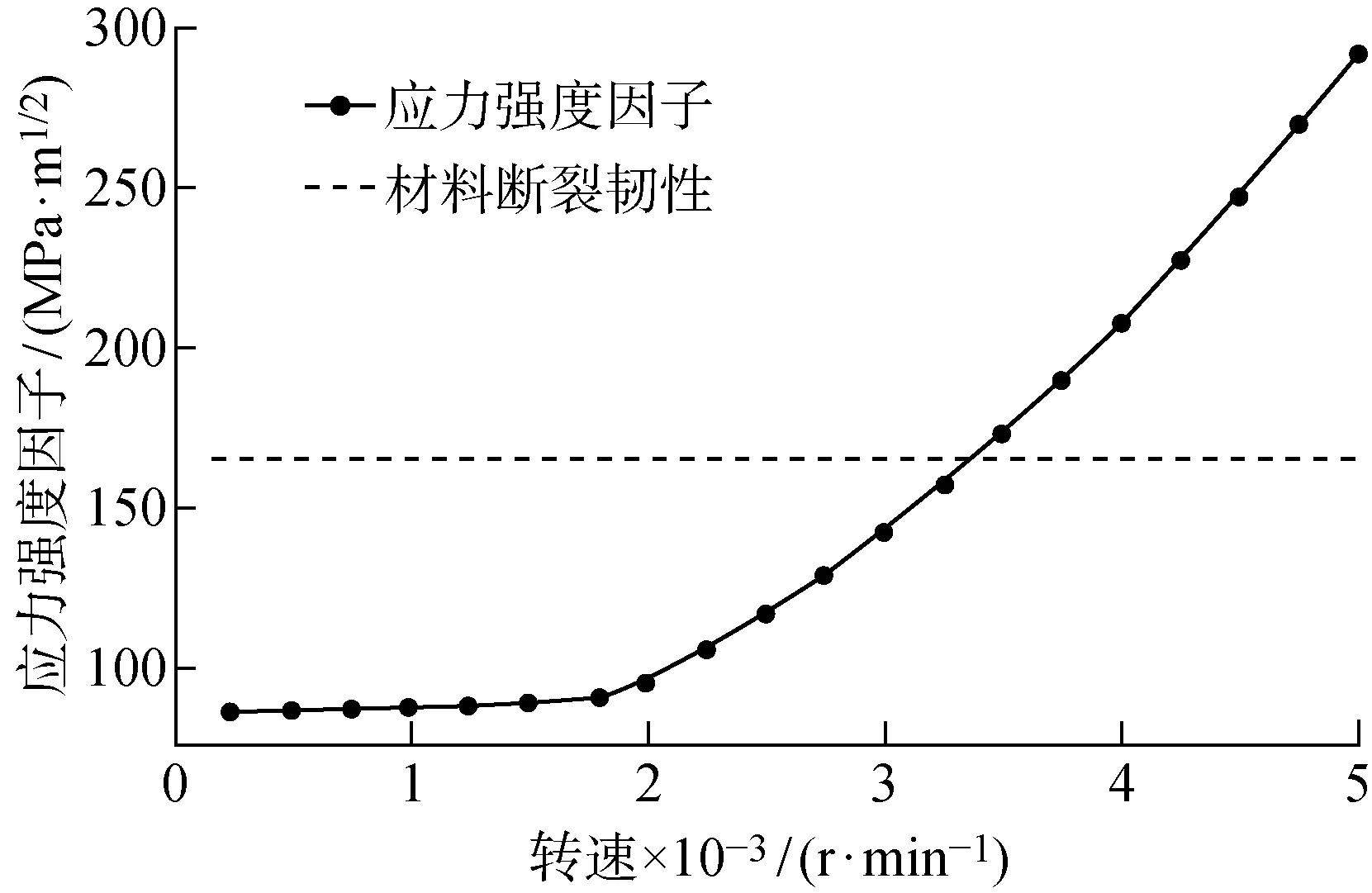
图7 应力强度因子与飞轮转速的关系Fig.7 Relationship between stress intensity factor and speed of crack

从图7中可以发现，当转速低于 1 800 r/min时，应力强度因子的增大较为缓慢，此时装配应力的大小对其起决定性作用.当转速高于 1 800 r/min时，应力强度因子的增大逐渐变快，此时离心力的大小开始占主导作用.与此同时，如果飞轮在达到设计转速(2 250 r/min)后仍可继续加速旋转，那么当转速达到约 3 200 r/min时，应力强度因子将会大于材料断裂韧性165 MPa·m1/2，此时保持环可能发生断裂.

2.2 应力强度因子与裂纹长度的关系

应力强度因子与裂纹长度之间的变化关系如图8所示.从图中可以发现，随着裂纹长度的增加，最大应力强度因子变化很小，因为该最大值出现在裂纹最深处，而非裂纹两端，所以最大应力强度因子的大小与裂纹长度并无明显关系.

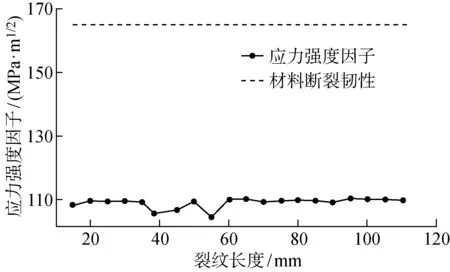
图8 应力强度因子与裂纹长度的关系Fig.8 Relationship between stress intensity factor and length of crack

2.3 应力强度因子与裂纹深度的关系

应力强度因子与裂纹深度之间的变化关系如图9所示.从图中可以发现，随着裂纹深度的增加，最大应力强度因子也随之增大，但逐渐趋于平缓，当裂纹深度达到约16 mm时，应力强度因子将会大于165 MPa·m1/2，此时保持环可能发生断裂.

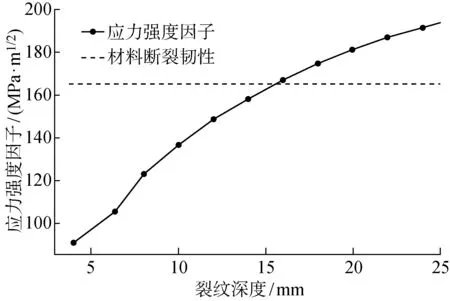
图9 应力强度因子与裂纹深度的关系Fig.9 Relationship between stress intensity factor and depth of crack

3 裂纹寿命评估

工程中广泛应用Paris公式[11]对裂纹进行寿命评估，这一公式能准确地描述中速率裂纹扩展阶段.在实际的工程应用中，这一阶段也是疲劳裂纹扩展寿命的重要研究阶段.其计算公式为

da/dN=C(ΔK)m

(1)

式中：a为裂纹深度；N为应力循环次数；da/dN为裂纹扩展速度；C和m均为材料常数；ΔK为应力强度因子幅，

(2)

式中：f为构件几何与裂纹尺寸函数；Kmax和Kmin分别为最大和最小应力强度因子；Δσ为裂纹处应力幅值.

为了计算裂纹在寿期内的循环次数，还需要知道临界裂纹深度ac，

(3)

式中：Kc为构件许用应力强度因子；σmax为最大循环应力.

式(2)和式(3)中均含有参数f和σ.f为构件几何以及裂纹尺寸的函数，其取值需要查阅应力强度因子手册[12]，但是该手册仅适用于结构以及受力简单的部件，对于屏蔽式核主泵飞轮并不适用.其次，对于结构不连续处的裂纹，σ的提取也存在困难，所以有必要对式(2)和(3)进行修正，重新计算应力强度因子，并结合Paris公式对飞轮的裂纹进行寿命评估.

为了计算ΔK，首先要确定应力循环.由于在稳态运行时，飞轮与一回路主冷却系统被主泵热屏隔开，并不会受到一回路温度扰动的影响，所以只需考虑应力强度因子在启停循环中的变化.结合图7可知，在启停的循环中，最大和最小应力强度因子分别出现在设计转速工况下(2 250 r/min)以及停机工况下(0 r/min).

为了得到Kmax和Kmin与裂纹尺寸a的关系，结合图9以及式(2)，本文对K～a1/2进行线性回归.首先考虑飞轮的设计转速工况(2 250 r/min)，此时Kmax关于a1/2的线性回归结果如图10所示，呈良好的线性关系，其回归方程为

Kmax=23.779+34.891a1/2

(4)

将保持环材料的断裂韧性代入式(4)中，即可计算得出飞轮临界裂纹尺寸ac=16.382 mm.

考虑飞轮的停机工况(0 r/min)，此时Kmin关于a1/2的线性回归结果如图11所示，其回归方程为

Kmin=16.127+27.994a1/2

(5)

结合式(4)和(5)可得ΔK的计算公式为

ΔK=7.652+6.897a1/2

(6)

将其代入式(1)并两边积分可得

(7)

查询文献[13]可得C=1.39×10-7,m=2.25，与初始裂纹尺寸a0=6.35 mm一并代入式(7)中，可得裂纹尺寸与启停循环次数的关系，如图12所示.图中，临界裂纹尺寸ac=16.382 mm，此时飞轮裂纹的循环寿命Nc=33 126 cycle(注：从初始裂纹尺寸6.35 mm开始计数)，大于设计规格书中所规定的 3 000 cycle[3]，说明飞轮在核主泵寿期内不会发生断裂事故.

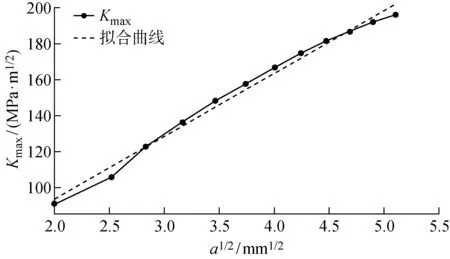
图10 Kmax关于a1/2线性回归Fig.10 Linear regression of Kmax on a1/2

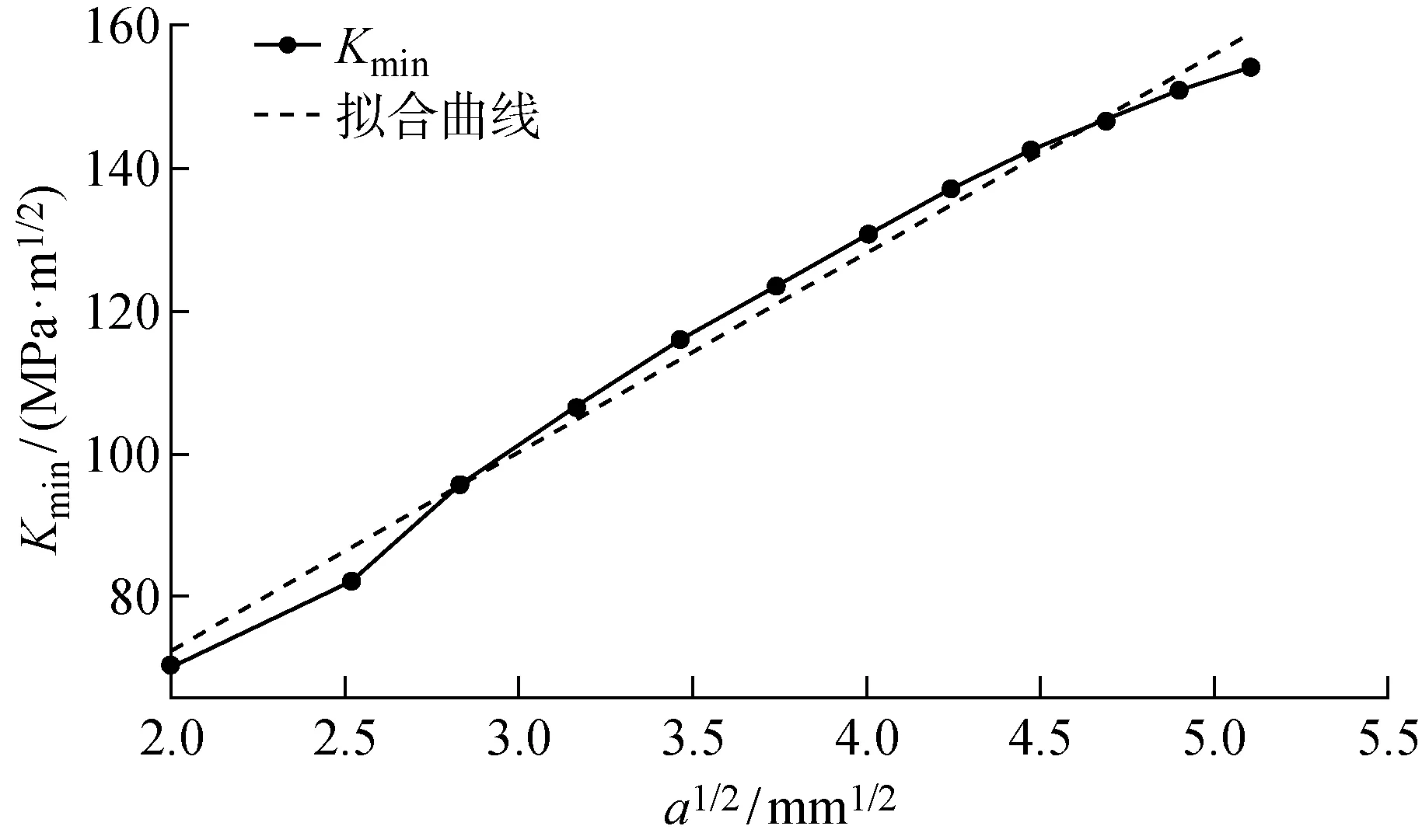
图11 Kmin关于a1/2线性回归Fig.11 Linear regression of Kmin on a1/2

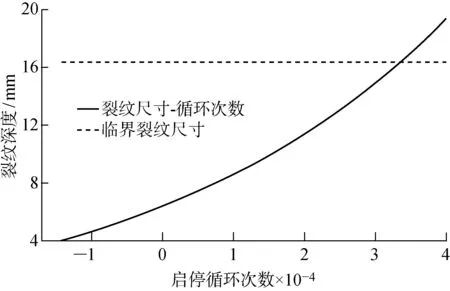
图12 裂纹深度与循环周期的关系Fig.12 Relationship between size and cycle of crack

最后对比式(2)和(6)可以发现，两者形式并不是完全相同，后者存在一常数项，而非完全的正比函数.这进一步说明将飞轮简化为半无限大体进行应力强度因子计算及寿命评估的可行性存在一定问题，计算结果存在一定的误差，本文则针对以上问题对原有计算公式进行修正，使得计算结果更为贴近实际工况.

4 结语

本文计算了飞轮裂纹的应力强度因子，并结合Paris公式对其进行寿命评估，有别于以往将飞轮简化为半无限大体的研究方法.本文在飞轮保持环内表面引入假想裂纹，建立了与实际飞轮结构相同的三维模型.根据传统的应力强度因子计算公式，应力强度因子K与裂纹深度的平方根a1/2之间呈正比关系.但是就结构和受力复杂的双金属飞轮而言，本文发现其应力强度因子K与裂纹深度的平方根a1/2之间呈良好的线性关系，对这一关系进行线性回归，得到应力强度因子K关于裂纹深度平方根a1/2的表达式，替代了只适用于理想构件的应力强度因子计算公式.最终通过Paris公式对飞轮裂纹进行寿命评估，得到了裂纹深度与循环周期之间的关系，同时结合K准则可知飞轮在核主泵寿期内不会发生断裂事故.