未知环境下水下机械手智能抓取的自适应阻抗控制
张建军, 刘卫东, 李 乐, 程瑞锋, 郑海峰
(西北工业大学 航海学院, 西安 710072)
在水下机械手采集水下样本的过程中,会出现操作对象未知以及操作不确定所引起的目标损坏或抓取不牢的问题,而含有力控制的柔顺性抓取方法能够解决机器手操作性不强的问题,其控制核心是自由空间的位置以及抓住过程的力的控制[1],主要控制方法包括阻抗控制、导纳控制与比例-积分-微分(PID)控制.其中,大多采用阻抗控制方法.阻抗控制是通过调节用户设定的目标阻抗模型以使机器人终端达到柔顺性目的的.很多学者利用阻抗控制方法对非水下环境的力、位移控制进行了研究,主要用于果蔬抓取[2]、患肢康复[3]、工件表面打磨[4]、轴孔装配和机器人行走等方面.例如:Hogan[5]提出的阻抗控制的基本思想是调整机器人末端刚度,以使力和位置满足某种理想的动态关系;Seul提出的阻抗控制方法能够实现自由空间的位置跟踪并将力信号控制在一定范围内,但无法保证力的精确控制[6];王学林等[7]将阻抗控制用于果蔬抓取,实现了机械手指端的期望抓取力的跟踪,但无法满足目标抓取的多样性;Dong等[8]建立了基于阻抗控制的模型参考神经自适应控制系统,以适应不同的环境.
为了实现机器手的抓住、抓牢控制并避免目标损伤,本文提出了一种自适应阻抗控制算法,建立了基于位置的阻抗控制模型,对抓取目标的阻抗参数进行在线辨识,利用机械手末端的运动特征与刚度的模糊辨识来调整期望抓取力,并根据期望抓取力与实际抓取力的误差设计自适应PID控制器,以实时调节期望位置,从而实现机械手在跟踪目标位置的同时对期望抓取力的跟踪.
1 数学模型
1.1 水下机械手的运动模型
水下机械手主要用于水下目标的采集.考虑到水下的复杂环境,本文只对1根含2个关节的手指进行研究,2个关节的手指可以简化为1个二连杆旋转机器人.与机器人的动力学模型相同,水下机械手的动力学模型可描述为
τ-JT(q)Fe
(1)
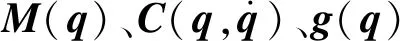
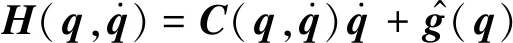
则机械手操作空间与关节空间的位置、速度和加速度可换算为
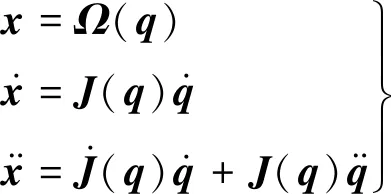
(2)
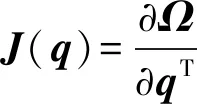
将式(2)代入式(1),所得在笛卡儿坐标系下机械手的动力学方程为
(3)
式中:下标x表示操作空间.将式(2)代入式(1),并与式(3)对比可得
(4)
1.2 环境模型
将抓取目标看成线性弹簧[9],在笛卡儿坐标系下,目标的抓取力为
(5)
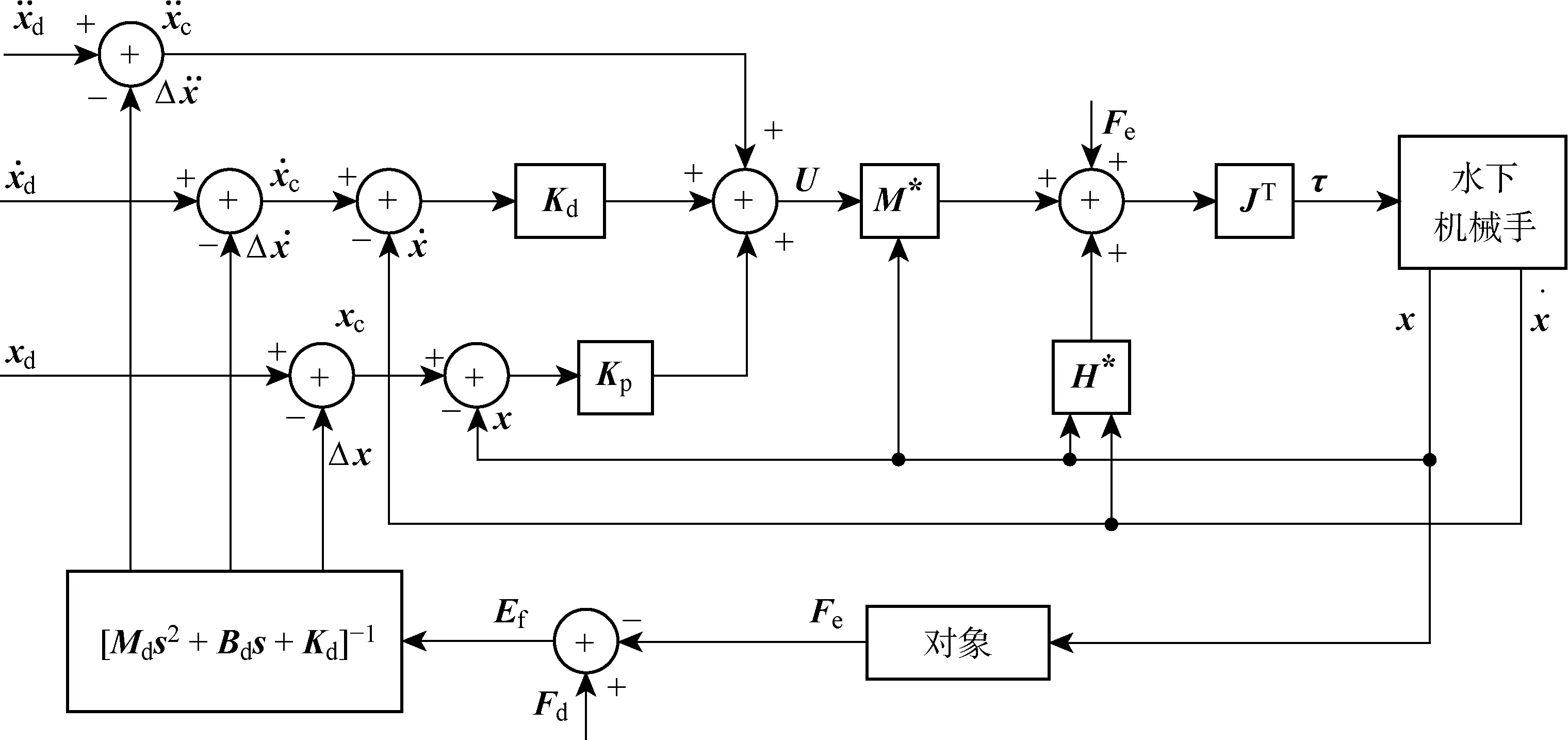
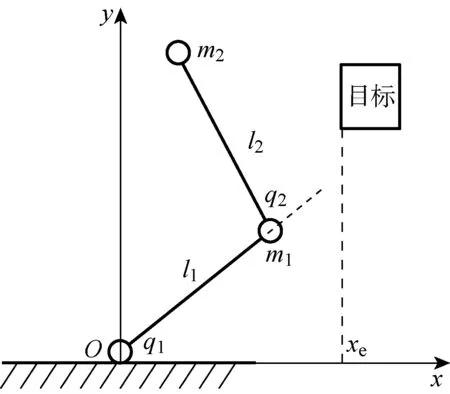
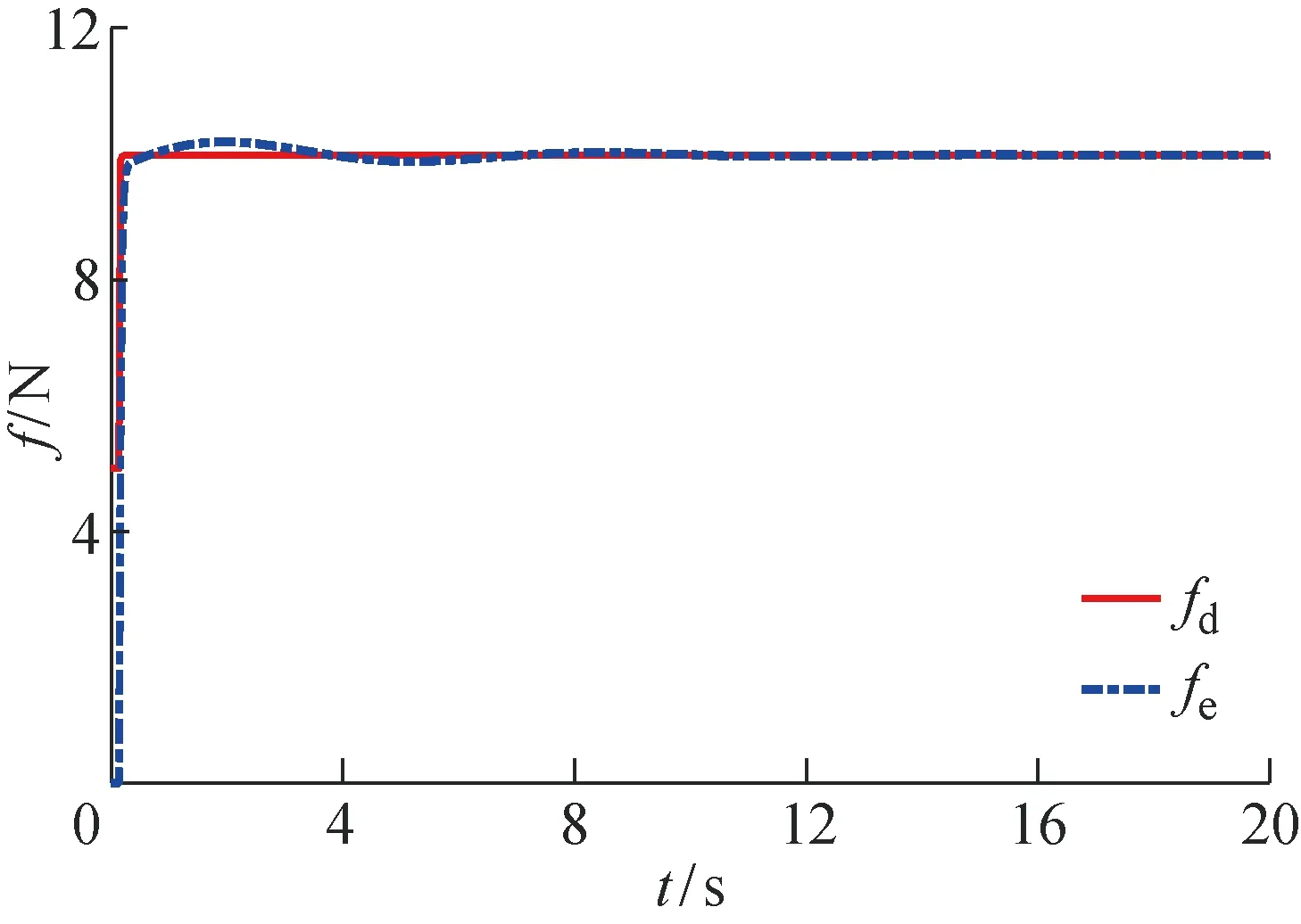
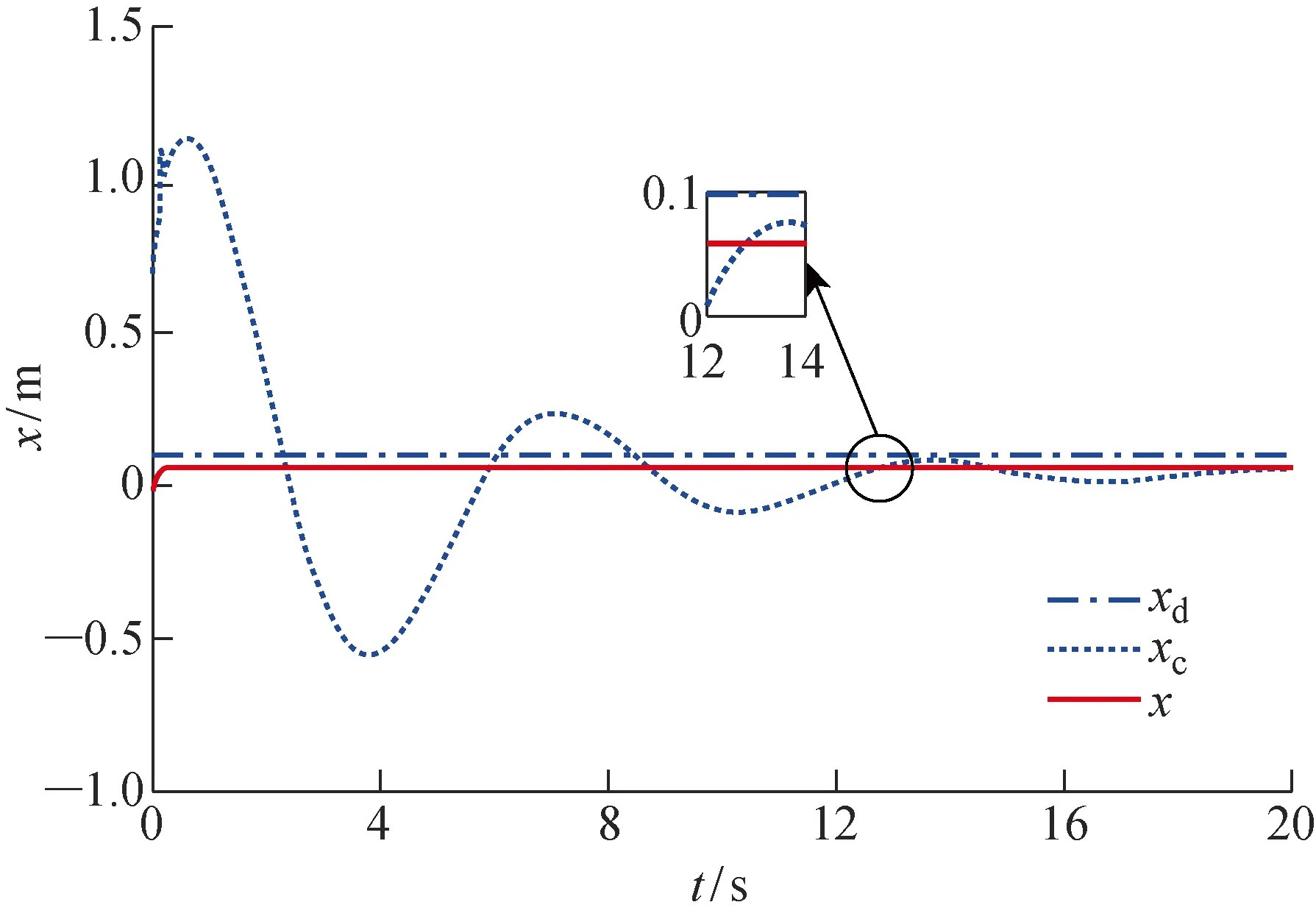
式中:xe为抓取目标的位置;ke为目标刚度系数.当x 在机械手末端执行器与抓取目标的相互作用力、末端位置偏差、速度偏差和加速度偏差之间建立一个2阶系统的控制模型,即描述阻抗控制的目标阻抗模型,其具体形式为 Kd(xd-x)=Fd-Fe (6) (7) 图1 基于位置的阻抗控制系统结构Fig.1 The impedance control system structure diagram based on position (8) 由2阶系统的稳定性可知,随着时间增加,x收敛于xc,以保证机械手对位置的准确跟踪.根据图1和式(7)及(8),所得整体的系统控制律为 (9) 不失一般性,只分析一维空间的情形.采用fd和fe分别表示机械手在x轴方向的期望抓取力与实际抓取力.固定的力和位置的期望值会给抓取力的跟踪带来静态误差,因此,设定机械手位置的期望值xd=xe+fe/ke,以确保力信号与位置信号的准确跟踪[10].其中,xd、xe和ke分别表示期望位置、抓取目标的实际位置及目标刚度系数的值.在实际中,无法获取xe与xd,且易造成跟踪的静态误差,只有实时调整期望位置,才能够实现对期望的抓取力与位置的跟踪.另外,采用固定的fd值无法满足目标抓取的多样性,所以通过辨识抓取目标的性能参数和模糊控制器的控制来在线调整fd值. 不失一般性,只分析一维空间的情形.为了实现期望抓取力的跟踪以及期望位置的控制,对抓取目标的参数进行在线辨识.本文采用递推最小二乘法辨识目标的刚度与阻尼.假设抓取目标具有阻抗特性,即为无源的,抓取目标为弹簧-阻尼模型,其接触时的抓取力可表示为 (10) 根据抓取目标的特征实时调整机械手末端与抓取目标之间的期望抓取力.根据抓取过程和抓取目标的阻抗特点,提出如下期望抓取力的在线模糊调整算法: fd(k)=fd(k-1)+γΔfc (11) 式中:fd(k)、fd(k-1)分别为k时刻以及k-1时刻机械手末端与抓取目标之间期望抓取力的值;γ∈[-1,1],为根据抓取目标阻抗参数调整的期望抓取力的调节系数;Δfc为常数,表示期望抓取力信号每次调节的最大值. 然后,根据以上模糊控制规则建立从输入到输出的模糊规则表. 本文设计了自适应PID算法以实现期望位置信号的自适应调整.在期望抓取力的跟踪位置xd加入调节信号[13],即 xd=xd0+Δxf (12) 式中:xd0为初始设定的期望位置;Δxf为期望位置的修正量,且 式(6)中的二维空间可以解耦成2个一维空间,在一维空间情形下的阻抗控制模型为 kd(xd-x)=fd-fe (13) 式中:md、bd、kd分别为期望惯性量、阻尼和刚度的一维表示形式. (14) 采用模型参考自适应控制方法和Lyapunov稳定性定理设计自适应阻抗控制律,式(14)为模型参考自适应控制中的可调系统.调整d(t)、c(t)和p(t),以缩小实际抓取力误差ef(t)与期望抓取力误差em(t)的差值,使得实际的系统响应跟随参考模型的响应.em(t)的轨迹取决于参考模型,将参考模型设计为理想的2阶系统,即 (15) 利用Lyapunov稳定性定理求解自适应律,令 (16) 则式(14)可简化为 (17) 由式(17)减去式(15),所得参考模型与实际模型误差方程的状态空间为 (18) (19) 式中: ω0、ω1和ω2均为任意的正数,P为任意一个非奇异正定矩阵.显然,V(Ee,t)具有正定性.对V(Ee,t)求导,可得 (20) 式中: (21) 系数χ(t)、d(t)、c(t)和p(t)的自适应调整率为 (22) 式中:λp、λv、η、μ1和μ2均为较小的正数;d0、c0和p0分别为d(t)、c(t)和p(t)在初始时刻的值. 分别根据期望抓取力与实际抓取力的误差对d(t)、c(t)和p(t)进行实时调整,将所得一个位置的较小修正量输入经典阻抗控制器的调整项中,从而达到了间接调整期望位置的目的. 图2 2自由度机械手仿真模型Fig.2 The simulation model of two degrees of freedom manipulator 图3 自适应控制抓取力的跟踪曲线Fig.3 The force tracking curves with adaptive control 图4 自适应控制位置的跟踪曲线Fig.4 The position tracking curves with adaptive control 实验1不加辨识,设定1个变化的力信号进行跟踪实验.假设在x轴方向的力的跟踪信号fd=10+sint,y轴方向的力为0,抓取目标的实际位置xe=0.05 m,期望位置xd=0.10 m,仿真结果如图3和4所示.由仿真结果可见,机械手的抓取满足对变化的力的跟踪要求,从而实现了机械手的抓取以及期望抓取力信号的控制. 图5 自适应控制目标阻抗的刚度辨识曲线Fig.5 The object impedance identification curves with adaptive control 图6 自适应控制抓取力的跟踪曲线Fig.6 The force tracking curves with adaptive control 图7 自适应控制位置的跟踪曲线Fig.7 The position tracking curves with adaptive control 实验2加入在线辨识的抓取目标阻抗,通过自适应调节期望的抓取力来实现机械手抓取力信号的跟踪.只考虑x方向的跟踪.设置xd=0.10 m,抓取力的初始值为5 N,xe=0.05 m,ke=1 kN/m,仿真结果分别如图5~7所示.由图5~7可见,所设计的自适应阻抗控制系统能够很好地辨识目标阻抗,根据阻抗参数模糊推理出需要抓取的目标的期望抓取力,并且能够实现期望的位置调整,保证了位置跟踪.另外,机械手在从自由空间到约束空间的过渡过程中,对抓取力控制的柔顺性很好,虽然在控制位置出现了一个小的抖动,但是不影响对实际位置的跟踪,从而满足了不但能够抓住而且能够控制抓取力的功能. 在传统阻抗控制方法的基础上,提出了自适应阻抗控制方法.以阻抗控制外环、位置控制内环为核心,分别设定期望抓取力与期望位置,利用递推最小二乘法在线辨识抓取目标的阻抗参数,根据辨识的目标阻抗特征与运动属性,通过模糊控制在线调节期望抓取力,采用自适应PID控制器实时调节期望位置,以实现在机械手跟踪期望位置的同时对期望抓取力的跟踪,从而满足对目标的抓住、抓牢并防止损伤目标的智能抓取功能.同时,通过在MATLAB/Simulink软件平台上进行仿真实验,验证了所提自适应阻抗控制方法的有效性.结果表明,所提自适应阻抗控制方法在自由空间和约束空间均具有良好的力、位移的跟踪性能.2 整体控制策略
2.1 阻抗控制模型
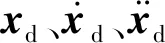
2.2 基于位置的阻抗控制
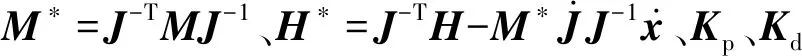
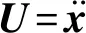
3 自适应阻抗控制的实现
3.1 递推最小二乘法的参数辨识

3.2 期望抓取力的模糊调整




3.3 期望位置的自适应调整
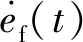
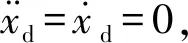

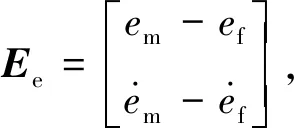
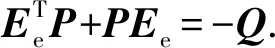
4 仿真实验
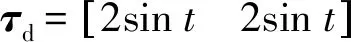



5 结语

