未知声速下长基线系统定位修正算法

黄 健， 严胜刚

(西北工业大学 航海学院， 西安 710072)

近年来，对水下目标的精确定位有着广泛的应用，如海底大地形变测量研究、近海勘探和海洋工程等[1-3].水下目标定位系统按照基线长度划分可分为长基线(LBL)系统, 短基线(SBL)系统和超短基线(USBL)系统3大类.相比之下，长基线系统具有更高的定位精度和更大的定位范围[4].

为了定位目标，LBL系统需要测量声信号在目标与水听器之间传播的到达时间(TOA)或到达时间差(TDOA)，这其中，基于TOA的长基线定位技术具备较高的精度和顽健性.在TOA估计过程之后，可以通过将TOA值和声速相乘来计算目标和水听器之间的距离，然后使用诸如非线性最小二乘法(NLS)、最大似然估计(ML)、线性最小二乘法(LLS)或加权线性最小二乘法(WLLS)等方法对目标进行定位.

不准确的声速是造成LBL系统定位误差的主要原因之一.在之前的研究中，距离的测量是基于声速是一个常数值，并且能被预先测量或准确估计这一前提[5].事实上，水下环境复杂，声速结构存在深度方向上的梯度[6]，这导致遵循Snell定律的声信号传播路径存在折射现象.使用恒定的声速并且假设声信号沿直线传播，必然会对LBL系统定位造成严重的误差.声速随深度的变化情况由声速剖面(SSP)表示，可通过声速分析器(SVP)测量，或由电导率、温度和密度(CTD)的测量值计算获得.然而，目标与水听器之间的平均声速却难以直接测量.因此，声速修正成为提高水下声学定位精度的关键技术之一.在之前的研究中，声速修正通常是在准确测量声速剖面的基础上，通过使用射线声学理论追踪声信号的传播路径来实现[7-12].为减小声速误差造成的影响，需要测量实际的声速剖面.然而，SVP或CTD测量的结果不可避免地存在误差.这导致基于固定声速剖面的声速修正方法性能的退化.在考虑声速未知的定位算法中，文献[13-14]将声速视为未知变量，并在定位的同时计算有效声速(ESS).然而，这类方法通常假设LBL系统中目标到任一水听器之间的声速相等，这也与理论和实际情况不符.

通过分析有效声速与目标和水听器相对位置之间的关系，本文提出一种基于粒子群优化(PSO)算法的LBL系统定位方法.首先，利用LBL系统中的冗余信息建立多参数优化函数来估计有效声速.其次，选择PSO算法来解算优化函数，得到目标与不同水听器之间的有效声速.最后，由所得有效声速对目标进行定位.仿真结果表明，该方法可以在无法准确获得声速剖面的情况下提高LBL系统定位精度.

1 问题描述

1.1 基于TOA的LBL系统定位原理

如图1所示，本文所使用的LBL系统由位于海面的4个浮标组成.每个浮标都配置有水听器和GPS设备，以便实时获取自身的位置.目标为位于海面以下的同步信标.定义坐标系如下：通过选择由4个浮标所围多边形中的某点作为原点O(0,0,0)来建立大地坐标系(NED).4个浮标的坐标分别为A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3)和D(x4,y4,z4).目标坐标为T(x,y,z)，每个浮标和目标之间的相对距离分别定义为R1,R2,R3和R4.

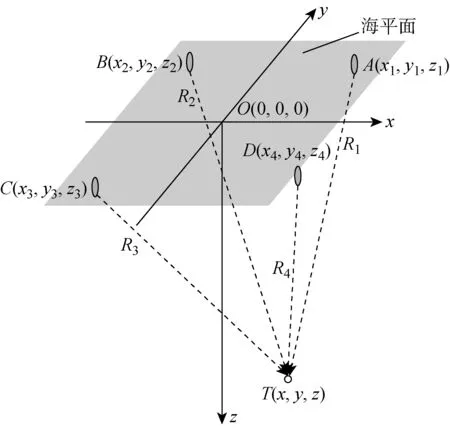
图1 LBL系统定位原理图Fig.1 Positioning principle diagram of LBL system

目标首先发射探测信号.由于目标与各浮标时间同步，浮标接收到该探测信号可以计算声信号的传播时间.将传播时间与平均声速相乘可以获得目标与各浮标之间的相对距离

(1)

在测量目标与浮标之间的相对距离后，它们之间的三维几何关系可以表示为

(2)

在LBL系统中，浮标与目标之间的相对距离通常为数百米到数十公里.因此，可以假设浮标位于相同的水平面，即

z-zi=z-zj,i≠j

(3)

将由2个不同的浮标建立的方程相减可以消除未知变量的二次项，进而获得如下的简化形式：

(4)

在声速已知的前提下，LBL系统的定位模型可以描述为如下函数：

(5)

(6)

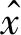
1.2 LBL系统中的有效声速

在传统的定位方法中，式(1)中的平均声速通常被定义为常量(1 500 m/s)，这无疑会导致较大的误差.根据射线声学理论，由声源发出的声信号会沿不同的路径传播到海洋中的任意一点，而这一点所接收到的声信号是全部本征声线的和.两点之间的有效声速则被定义为最先到达的本征声线所对应的等效声速，即声源与接收点之间的斜距与声信号最小传播时间的比值[15].若声速剖面已知，声信号在声源和接收点之间的传播路径可以通过Snell定律进行追踪，并由此计算两点之间的有效声速.通过调整初始入射角，可以迭代计算定位区域内任意两点间的有效声速.在准确获得有效声速之后，使用它们来代替式(1)中的平均声速可以提高LS方法的定位精度.

海洋中的有效声速不仅由声速剖面决定，还取决于两点之间的相对位置关系(水平距离、深度差和俯仰角等).本文设计了一个实验来测试当声源位于海面，目标点位于800 m深处时，海洋中两点之间的有效声速c与水平距离d的关系，实验结果如图2所示.其中，图2(a)为实验区域内的声速剖面，h为水深.选择BELLHOP[16]模型计算声信号传播时间，BELLHOP模型是水声信道仿真中应用最广泛的模型之一，该模型以海洋环境文件(包括声速剖面，海面/海底反射系数等因素)作为输入，通过对声场模型进行计算可得到传播损失、本征声线以及声线到达时间序列等多种实用数据，是声场建模及分析的一种有效手段.计算得到的有效声速如图2(b)所示.可以看出，在深度一定的情况下，不同的水平距离对应不同的有效声速值，且差别较大(在水平距离相差4 km的情况下，有效声速相差接近3 m/s).由此可以看出，若假设长基线系统的定位区域内目标到任一浮标的声信号传播速度相等会造成较大定位误差.

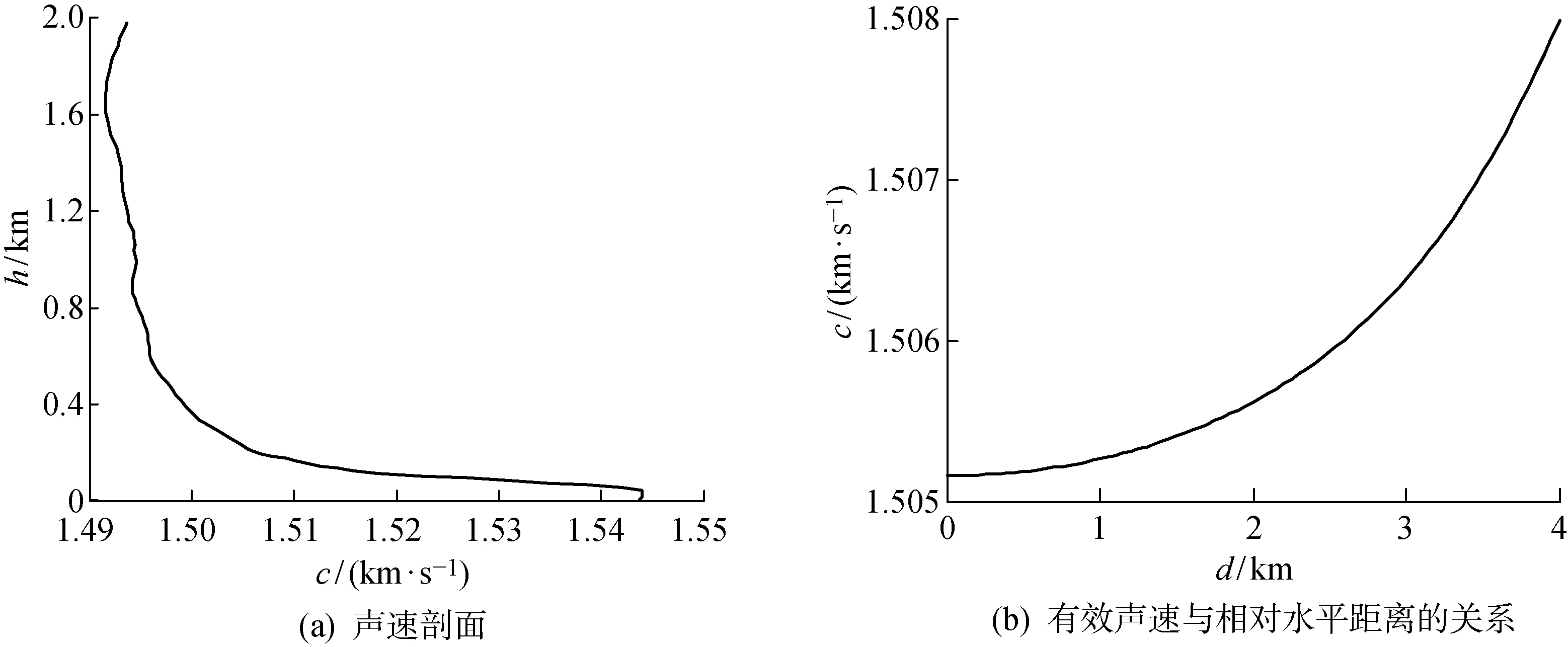
图2 有效声速与相对水平距离的关系Fig.2 The relationship between ESS and horizontal distance

1.3 定位模型

在如图1所示的LBL系统中，虽然目标与每个浮标之间的深度差是相等的，但由于水平距离不同，相应的有效声速也不相等.这导致使用单个有效声速的LS方法会产生较大误差.因此，通过设置声信号在目标和不同浮标之间以不同的有效声速传播来提高LBL系统的定位精度.

如图1所示，4个浮标位于海面，目标位于水下一定深度，其深度值可以通过深度传感器测量，并通过水声通信技术传输至控制中心.通过这种方式，目标的三维定位可以转换为二维定位问题.本文仅考虑目标位于LBL系统定位区域内的情况.

图3所示为LBL定位系统的二维原理图，其中4个浮标的坐标分别为：B1=(0,0,0)、B2=(L,0,0)、B3=(L,L,0)和B4=(0,L,0)，L=8 km为基线长度.图中的4个圆是以每个浮标为中心，以目标到每个浮标之间水平距离为半径所绘.这些水平距离是根据测量的传播时间和目标深度计算的.在有效声速估计精确的理想情况下，4个圆应相交在一点，即目标的真实位置.

图3 LBL定位系统的二维原理图Fig.3 2-dimensional positioning diagram of LBL system

然而，当有效声速估计出现误差时，4个圆不会在一点相交，而是围成一个小的区域.这将难以准确估计目标的真实位置.为此，本文通过缩小4个圆的相交区域来建立适应度函数.在LS算法中，3个浮标即可用于估计目标位置.因此，4个浮标可以通过不同的组合而获得4个不同的定位结果.将式(1)～式(6)定义的算法定义为函数LS(·)，4个定位结果如下：

(7)

在此基础上，本文给出如下适应度函数：

(8)

2 基于PSO算法的LBL系统定位

本文利用PSO算法解决多参数优化问题. PSO算法是Kennedy于1995年提出的随机优化算法.在PSO算法中，优化问题的解决方案被视为搜索空间中的粒子，并通过迭代跟踪目前搜寻到的最优值来找到全局最优解.PSO算法精度高，收敛快且易于实现，近年来，已经得到广泛的研究和发展，显示出其解决随机优化问题的优势.

PSO由一组粒子构成，每一个粒子都是优化问题的备选解.粒子有自身的位置和速度矢量，矢量大小取决于优化问题所包含的参数.在PSO的每一轮迭代中，粒子通过跟踪自身的历史最优解和全局最优解来更新其位置，并分别通过式(9)和(10)来更新其速度和位置矢量.即

式中：v为速度矢量；x为位置矢量；下标Id为粒子标识；ω为惯性权重，常用来平衡粒子群的全局搜索能力和局部搜索能力；η1和η2均为在[0, 4]范围内的学习因子，通常取η1=η2=2；rrand1和rrand2均为[0, 1]内均匀分布的随机浮点数，它们赋予粒子在搜索空间内移动的能力；pbestId为粒子迄今为止已经获得的最佳位置向量；gbest为整个粒子群的全局最优位置向量，迭代次数可以预先确定或根据适应度函数的收敛来动态调整，当满足停止条件时，gbest中存储的即为优化问题的最优解.

2.1 粒子位置向量的设置和初始化

为了简化计算，设置目标与各浮标间的有效声速组成的一维向量作为粒子在使用PSO算法求解适应度函数的过程中使用的位置向量，即

x=[c1c2c3c4]

(11)

式中:c1、c2、c3和c4均为目标与对应浮标之间有效声速的估计值.

在PSO算法的开始，需要初始化粒子的位置矢量，可以根据经验选择声速的搜索空间，并在搜索空间内随机初始化粒子的位置矢量.

2.2 约束条件

PSO算法的约束条件：

(1) 声速限制.海洋中的声速值有一定的范围，不会太大或太小.因此，将这个算法中的声速限制在如下范围内：

cmin≤ci≤cmax

(12)

(2) 定位点之间几何位置关系的约束.有效声速的估计应受目标和浮标之间的位置关系的限制，在实际操作过程中，应根据浮标的排列来对有效声速的估计值加入一定约束条件.以图3所示的LBL系统为例，由两个相邻浮标确定的圆仅在LBL定位区域内的一个点处相交，并且这些交点的位置具有一些几何关系约束.例如，由浮标1和浮标2形成的交点应比由浮标3和浮标4形成的交点具有更小的y值，否则有效声速的估计值将过大.令E(·)表示由任意两个浮标的圆确定的交点，可以得到以下的约束条件：

(13)

2.3 终止条件

PSO算法的终止条件：

F≤TH

(14)

式中：TH为一阈值，决定了在PSO算法收敛时由式(7)给出定位点所围成多边形区域的大小.由于在LBL系统中，定位精度与时延估计精度有关，而时延估计的精度与目标距离成反比，距离越远则时延估计精度越低.因此，TH值可以在PSO算法开始之前由LBL系统的基线长度确定.

2.4 算法流程

在基于PSO的LBL系统定位方法中， PSO被用来计算目标与各水听器间的有效声速.在迭代结束时，gbest存储了有效声速的估计结果.最后在获得有效声速的基础上，使用LS算法来估计目标的坐标.基于PSO的LBL系统定位方法步骤如下：

(1) 输入已知参数.定义所需变量并随机生成具有N个粒子的种群，随机初始化每个粒子的位置和速度.

(2) 计算每个粒子的适应度值，分别存储每个粒子当前的最优历史解和全局最优解.

(3) 根据式(9)和(10)更新每个粒子的速度和位置.

(4) 判断算法是否满足停止条件.如果满足，则进行下一步，否则转到步骤(2).

(5) 输出全局最优个体，即各有效声速的估计值，然后可以通过LS算法对目标进行定位.

3 仿真结果与分析

通过仿真实验来测试本文提出方法的性能.实验环境：CPU为Intel Core i7-4710MQ; 内存为DDR3L-8 GB.操作系统为Windows 8.1；MATLAB 版本为R2014a.实验中，LBL系统的浮标布置仍如图1所示.基线长度设定为L=8 km.声信号在水下的传播时间由BELLHOP模型计算，并假设信标所测量的时延中包含服从N(0,σ2)分布的高斯白噪声，其中:σ=0.5 ms.所用的声速剖面如图2(a)所示.因为目标配置有深度传感器，可以准确地测量其深度值，所以本文只估计其二维坐标(x,y).

在使用LS方法的定位过程中，恒定声速取为 1.505 km/s，即图2(a)所示声速剖面在目标深度上的加权平均声速[17].PSO算法中粒子的数量选择为50.最大迭代次数设置为100，学习因子η1和η2都取为 2.0，惯性权重设置为 0.9，有效声速的搜索空间限制在声速剖面的最小值与最大值之间，即 1.495 km/s≤ci≤1.545 km/s，终止条件中令TH=1 m.

3.1 定位精度测试

令目标三维坐标为(3.25 km，4.30 km，0.80 km).定位结果如图4(a)所示.图中：4条线是4个定位圆的局部放大图；“+”号表示目标的实际位置；“o”是LS方法的定位结果(3.266 km，4.294 km)，其与目标真实坐标之间的距离为 16.58 km.

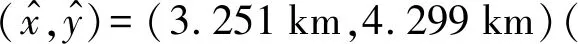
图4 定位结果Fig.4 Positioning results

本文通过在LBL系统的定位区域中随机选择10个点来比较基于PSO的方法和LS方法的定位精度.目标的深度为800 m，水平坐标在表1中列出.对于每个目标点分别使用LS方法和基于PSO的方法对其进行定位，且2种方法均独立运行50次.最后，计算2种方法定位误差的均方根误差(RMSE)以及定位误差的标准差(STD)，以评估其定位性能.定位误差的均方根误差为

(15)

式中：(x,y)为目标的真实位置；E[·]为求数学期望的算子.

仿真结果如图5所示.可以看出，LS方法由于无法获得准确声速，且采用单一声速进行定位，造成其定位结果距离误差较大，且目标的位置也会对结果产生一定的影响，难以获得理想的结果.而基于PSO的方法在定位的同时对有效声速进行调整，可以明显降低定位误差，并且可以看出误差独立于目标的位置，说明其定位的稳定性更好.

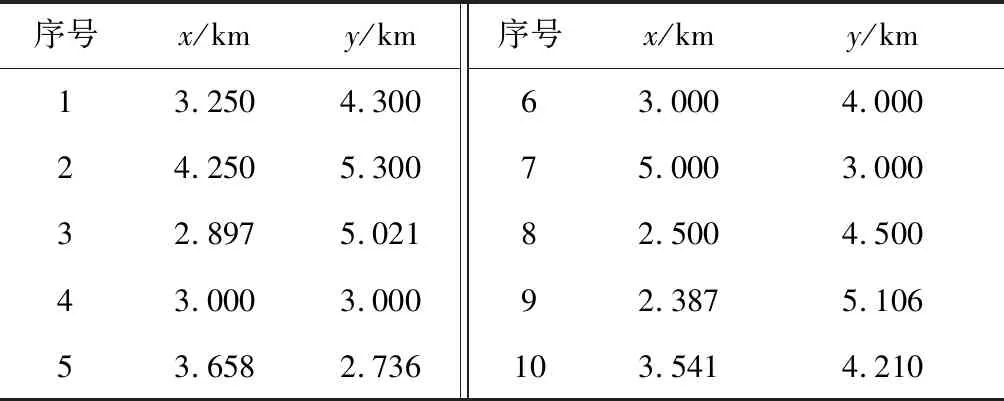
表1 测试点坐标Tab.1 The coordinates of target points

图5 仿真结果Fig.5 Simulation results

3.2 收敛性测试

PSO算法的收敛速度是实际应用中需要重点考虑的因素之一.本文分析上述多个点定位实验中PSO算法迭代过程的平均适应度值，为了获得每次迭代的适应度值，实验中令TH=0，测试结果如图6所示.

图6 平均适应度随迭代次数变化的曲线Fig.6 The changing of average fitness value with number of iterations

由图6可以看出，PSO算法可以在24次迭代左右达到收敛，且收敛后的适应度值小于1 m.由此也可以看出实验中设置终止条件为F≤1 m是合适的.

另外，本文还测试了运行PSO算法所耗费的时间，在模拟环境下运行基于PSO的方法一次的时间约为2 s，虽然比LS方法慢，但比常规测量声速剖面再进行声线跟踪的定位方法更快.

4 结语

本文通过使用PSO算法，实现了声速不确定情况下LBL系统定位精度的显著提高.传统LBL系统定位方法通常设定单个恒定声速值，并求解线性或非线性方程组来定位目标.这些方法不仅难以确定声速，而且与实际情况有很大的差异，导致定位精度较差.本文提出了一种基于PSO算法的LBL系统定位方法.该方法通过设置每个应答器和目标之间的声信号传播速度不相等来建立多参数优化问题，并利用PSO算法来解算得到有效声速，再由得到的有效声速对目标进行定位.仿真实验结果表明，所提出的算法具有比传统算法更高的定位精度和更好的稳定性，且计算效率足够高.这表明该算法适用于解决无法获得精确声速剖面情况下的LBL系统定位问题.