基于OpenFOAM的破损船舶横摇阻尼

欧 珊， 毛筱菲， 刘祖源， 黄天奇， 余泽爽

(武汉理工大学 交通学院， 武汉 430063)

船舶横摇阻尼具有非线性和复杂性，对船舶运动的预报及稳性的衡准有重要意义，也是一直以来备受关注的问题，一是对其准确预报在理论上非常困难，而且其非线性使问题变得非常复杂；二是阻尼对横摇运动影响巨大，研究横摇通常都要对阻尼进行讨论，因此对横摇阻尼的预报是横摇运动研究的基础.

以往的研究中解决横摇阻尼问题，一种方法是采用经验公式进行求解，如贝尔登公式，尼古拉夫公式，米勒公式，渡边公式等，还有IKEDA[1]总结的阻尼公式.基于经验公式，2011年第26届国际拖曳水池会议(ITTC)给出了横摇阻尼的数值估算[2].另一种方法是通过船模水池试验进行确定，分为船模静水中自由横摇衰减和强迫振荡运动试验，应用能量法来处理.其中，基于船模静水中自由横摇衰减得到横摇阻尼是目前较为常用的方法，但自由衰减试验只能给出在共振频率处的船舶阻尼，缺乏频率的相关性；强迫振荡试验虽能给出多个频率下的附加质量和阻尼，试验结果的分析仍然会受子样的限制，另外船模的强迫振荡运动对试验设备、测试系统要求较高，目前仍有许多学者致力于试验测试系统的研究.

随着计算流体动力学(CFD)方法在船舶领域的应用日益广泛，涌现出基于雷诺时均(RANS)方程求解船舶横摇阻尼的研究.最初在二维船体剖面上的研究较多，如文献[3]和[4].但横摇问题的三维流动特征明显，对船舶进行三维模拟更有必要.目前对三维船舶的横摇研究逐渐增多，基于RANS方程求解方法，Wilson等[5]对 DTMB5512 船进行了自由横摇和强迫横摇模拟，并应用ITTC关于CFD不确定度分析规程对模拟结果进行了验证和确认.国内应用RANS法进行船舶横摇阻尼的三维数值模拟的研究[6-9]，涉及船型、网格、航速、强迫横摇或自由衰减以及阻尼数据处理方法等各个方面.可见，CFD方法在研究横摇阻尼中已经比较普遍，但针对破损船的横摇阻尼研究较少.目前针对破损船舶的运动模拟仍有许多是基于势流理论，在计及黏性阻尼影响时几乎都采用经验或半经验公式，本文基于此，从破损角度来探讨横摇阻尼的特性.

破损的情况很复杂，一般将船舶的破损分为3类：第一类为破损进水后海水全部充满舱室，不存在自由液面；第二类为舱室局部被淹，而且不与舷外海水相通；第三类为舱室局部被淹并与舷外海水相连通.其中第二类和第三类较常见，本文主要研究这2类破损情况.

第二类破损为内外水耦合问题.船舶与水舱的耦合运动是极为复杂的流体动力学问题，船舶的运动影响水舱内水的流动，水的流动反过来影响船舶的运动.目前还没有从根本上解决这个问题，但是基于各种假设已有很多的处理方法，一般是将船和水舱分开进行水动力数值模拟，包括势流方法和黏性方法，也有将两者相结合的方法，然后将水舱产生的力和力矩作为外力作用于船舶上从而耦合船舶的运动，并从时域范畴步进求解[10].但是分开处理的方法作了较多假设，与实际有所出入，不能保证时域中每个时间步长都准确求解船舶的运动，而且对于船舶的横摇运动模态，用势流方法求解两者的耦合运动仍有不妥.

第三类破损为内外水相通问题.由于舱内水与舷外水相通，在船舶运动过程中舱室进水具有动态特征，进水的流入流出问题导致这类破损不适合用传统的准静态方法进行模拟，即假定破损船舶的进水达到稳定之后将舱内水视为液面水平且质量集中于一点，再进行动力响应分析.这种模型简化了复杂条件，在实际应用上有优势，但是其自由液面水平的假定并不符合物理情形，基于这样假定得到的舱内水的运动学和动力学结果是不够精确的，进而导致船舶运动预报的不准确.

因此，发展基于黏性流理论的破损水动力方法将成为今后的研究重点.本文在应用OpenFOAM对完整船舶的横摇阻尼研究基础上，进一步针对第二类和第三类破损船开展纯黏性的横摇数值模拟，重点研究破损后的横摇阻尼.一方面由于破损船的横摇阻尼的数值研究目前较少，多为试验研究；另一方面国际海事组织(IMO)第二代完整稳性完成后对新一代基于性能的破损稳性衡准也将提上日程，由此开展破损船舶的横摇阻尼的数值研究，并结合试验进行探索.

1 数值计算模型

1.1 研究对象

以一艘围网渔船为研究对象，通过对船体结构布置及规范要求的考虑，最终以船中处附近5号渔舱右舱破损开口为例，开口尺寸及位置信息见表1(以船底为参考平面).其中，5号渔舱的2种破损类型在模型处理方式上有所不同：

根据第二类破损定义可知，该类破损实际上与完整船舶舱室存在自由液面的情况类似，如载液舱、减摇水舱.由于涉及舱室内外水耦合的复杂问题，直接的数值模拟存在诸多困难，所以在模型处理上，通过一方柱孔(尺寸为 0.04 m×0.04 m×0.092 m)连通破损舱室内部与甲板外部，人为使计算域网格连续化，船体外表面仍保持完整光滑，如图1所示.在与物理模型接近的情况下，这种方法可以将非连续的多域问题简化为连续的单域问题，而不改变问题属性[11].

根据第三类破损定义可知，该类破损舱室的内外海水是连通的，船体外表面出现破损开口，但由于船体内外海水互通，在数值建模时可以将破损开口处的舱室内壁面作为船体外表面，这样既使船体外表面保持连续性，也保证数值模型的单域特征.所以在模型处理上直接将破损舱室内壁定义为船体外表面再对整船进行建模和网格划分，如图2所示.

通过CATIA对破损船进行物理建模，将模型文件以STL的格式导入OpenFOAM中进行六面体网格划分，采用OpenFOAM自带的网格绘制命令BlockMesh和SnappyHexMesh.由于渔船的模型存在附体舭龙骨，所以在绘制网格时必须要保证舭龙骨的表面不失真，这就要在不增加网格数量的情况下合理设置网格大小以及对船体表面进行“面加密”，如图3所示.

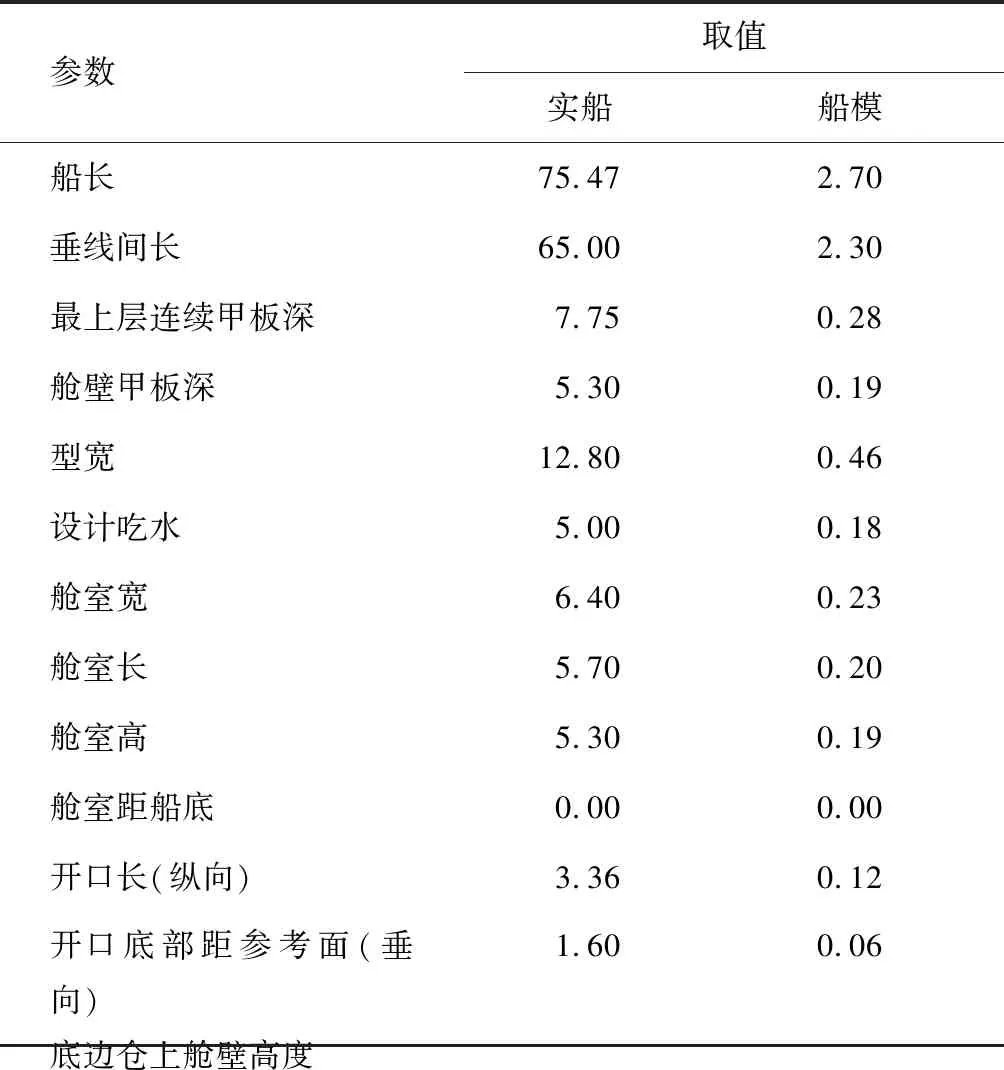
表1 围网渔船5号渔舱破损位置及开口尺寸Tab.1 The parameters of damaged fishing compartment m

图1 围网渔船第二类破损模型Fig.1 The second situation of damage

图2 围网渔船第三类破损模型Fig.2 The third situation of damage

图3 围网渔船船体表面网格Fig.3 Grid of hull surface

1.2 控制方程及参数设置

基于黏性流理论，以雷诺平均的N-S方程为控制方程:

(1)

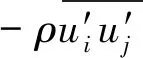
OpenFOAM程序库中的interDyMFoam求解器是在自由面求解器interFoam基础上调用了网格运动模块建立的，它是求解一类不可压缩不可渗透恒温的两相流问题的求解器.本文采用基于求解器interDyMFoam建立的waveDyMFoam程序库进行横摇的数值模拟，采用流体体积(VOF)方法捕捉自由液面，运用动网格技术包括自适应重划分网格的网格运动和网格拓扑变化，不仅可以实现船舶六自由度运动模拟也能实现数值造波.

本文主要研究静水中的自由衰减问题，湍流模型采用SSTk-ω模型，压力场和速度场的耦合迭代求解采用PIMPLE算法，时间离散采用欧拉线性的离散方式，梯度项采用高斯线性差值方式，计算控制设置库朗数为5，最大时间步长为 0.01 s，计算步长采用可变运行时间，过程文件输出间隔为 0.2 s.

另外，针对自由横摇衰减运动的模拟需讨论初始横摇角的给定方式.通常计算自由衰减会采用2种方案：第一种是给定初始横倾角，在数值模拟中，加载初始角的方法就是把船体三维模型旋转一定的角度，这种方式跟试验状态接近，但存在的缺点是在初始横倾时刻网格无变形，而当船舶从初始横倾侧运动到另一侧时网格变形过大，小角度情况下问题不大，但对大角度横摇就不太适合；第二种是给定初始角速度，在初始时刻船体正浮，给船体一个横摇的角速度，使之达到横倾的目的，优点是省时省力，缺点是无法精确控制初始横摇角度的大小，需要进行试算总结出适合该算例的规律.在实际工作中，根据对2种方案大量的数据对比发现，计算的阻尼结果差别并不大，所以为了减少工作量，自由横摇衰减的模拟均采用第二种加载初始角速度的方式.

1.3 网格讨论

在网格划分中，破损船相比完整船不同的是内部网格的绘制，需要设置合理的边界层参数，同时，在动网格迭代时对于不同的进水量选取合理的迭代因子，否则计算结果容易发散.对于破舱内水深的设置，利用文件setFieldsdict单独设置舱内的液体初始条件，并在SnappyHexMesh文件中调整面精度数、边缘精度以及其他的网格因素.

图4 围网渔船第二类破损开口处网格划分细节图Fig.4 Detail diagram of grid generation for the second situation of damage

图4和5分别为围网渔船第二和第三类破损开口处网格划分细节图.船模计算域尺寸为-L～3L(x轴方向)，-L～L(y轴方向)，-2L～L(z轴方向)，L为船长.考虑船舶横摇辐射兴波经壁面反射对船体运动计算的影响进行消波处理，采用的消波方法是在Mayer消波法上的拓展，其原理是增加松弛函数来消波.另外，局部细化自由面及船体附近网格，以精确捕捉自由表面和船体附近流场信息.需要指出的是，为了便于网格的划分，在破损模型中舱室内部结构做了简化处理，如图6所示.

图5 围网渔船第三类破损开口处网格划分细节图Fig.5 Detail diagram of grid generation for the third situation of damage

通过对图7三种不同网格方案(从左至右:细网格 4.08×106；中等网格 2.14×106；粗网格 1.27×106)进行数值计算后，分析横摇和垂荡运动对网格的依赖性，如图8所示.综合考虑精度和时间因素，选择中等网格作为本文最终的网格方案，其中第二类破损总网格数在 2.1×106，第三类破损总网格数在 2.14×106，网格最小尺寸为 0.012 m.

图7 三种网格方案Fig.7 Three schemes of computational grid

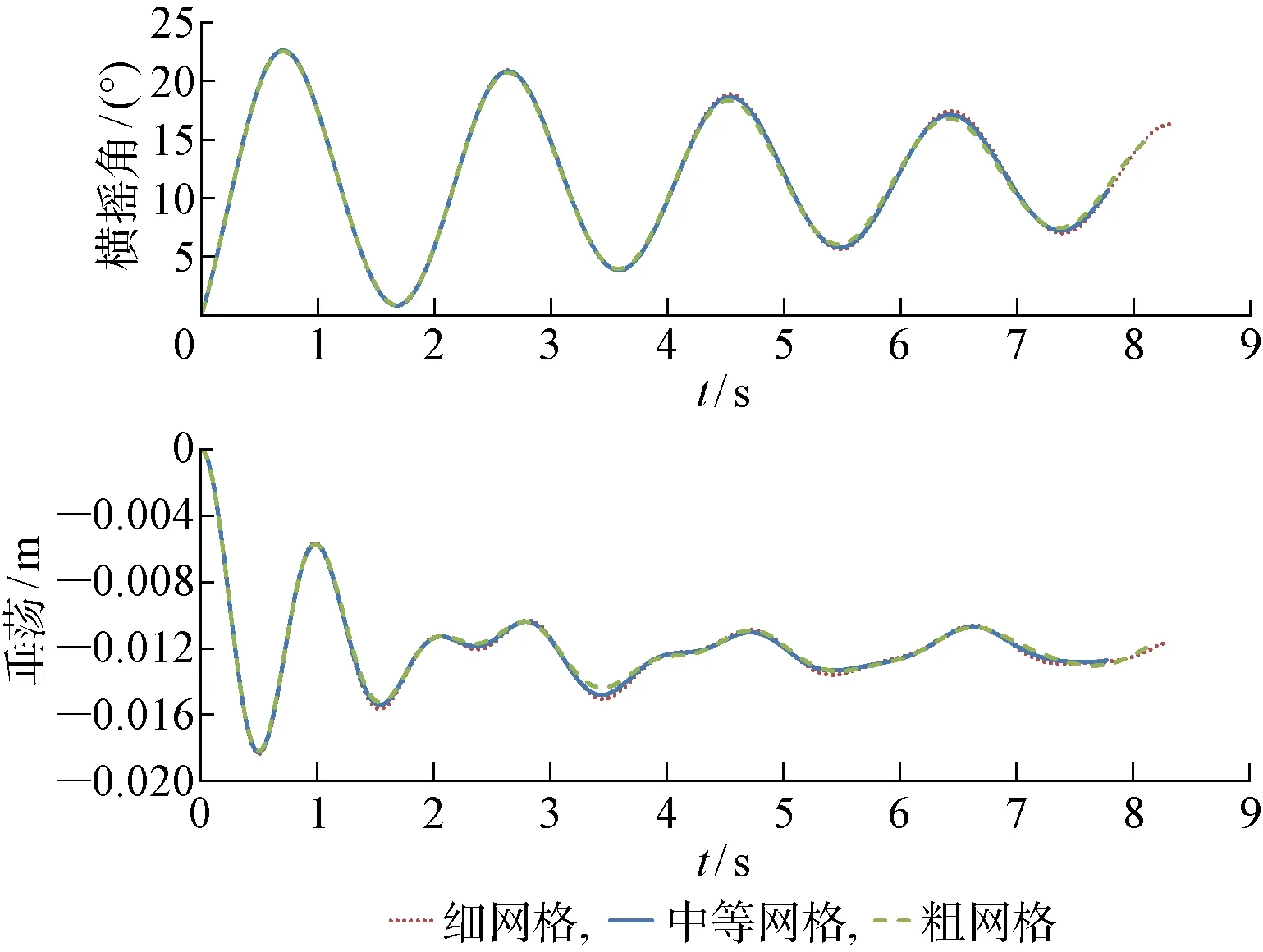
图8 三种网格下的横摇和垂荡运动数值对比Fig.8 Comparison of roll and heave motion under three different schemes of computational grid

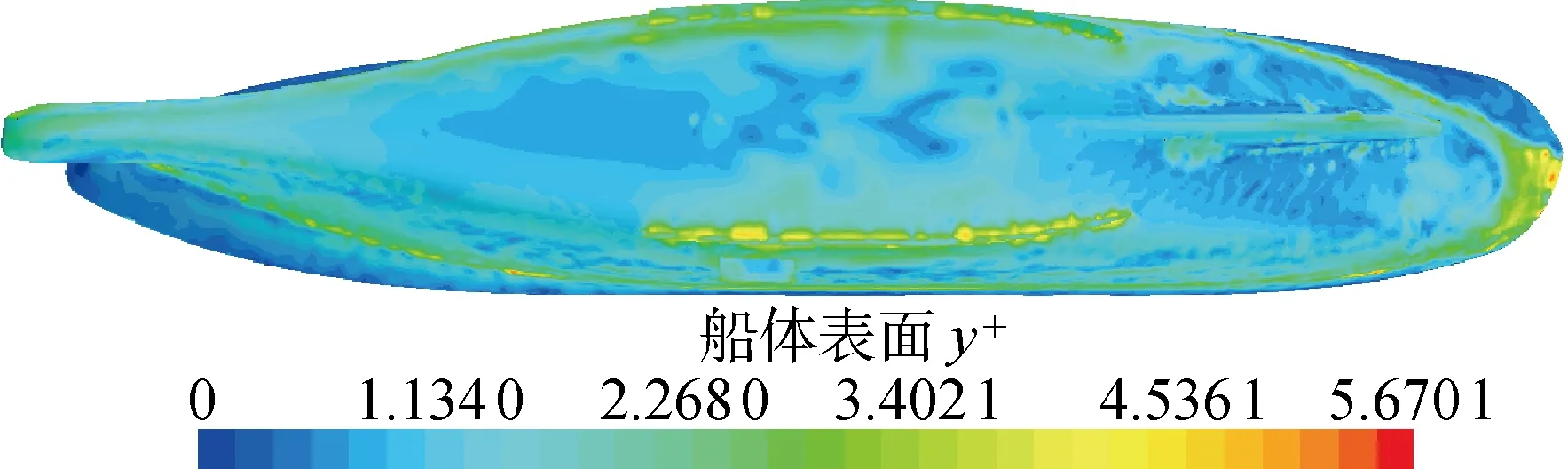
图9 y+分布Fig.9 y+ contour

近壁面流动的准确捕捉对有物面边界限制的湍流模拟至关重要，目前工程应用中大多采用壁面函数法或低雷诺数模型来处理近壁区域流动的求解问题.本文采用低雷诺数湍流模型SSTk-ω，通过边界层中数值求解RANS方程实现近壁面流动的模拟.近壁面的网格法向尺度如图9所示，可见：船体表面的壁面函数值y+值在绝大部分区域约为1，在船中及尾部的小部分区域最大值约为5.

2 数值模拟结果与分析

2.1 完整船静水自由横摇衰减数值模拟

基于以上的理论基础和数值模型，首先对船舶静水自由横摇衰减进行CFD模拟.为研究横摇阻尼的非线性特征设置系列初始横摇角，得到系列自由横摇衰减运动随时间t的幅值，如图10和图11所示.通过横摇消灭曲线拟合方法计算分析出线性阻尼和非线性阻尼2种成分阻尼(具体方法见文献[12])，并与基于实验流体动力学(EFD)的模型试验结果进行对比，汇总如表2.从中得到如下结论：

(1) 从与试验结果对比中可以看出自由衰减的数值模拟结果能较好吻合模型试验结果，横摇固有周期几乎一致，阻尼系数非常接近，验证了该方法在预报横摇阻尼研究上的可靠度.

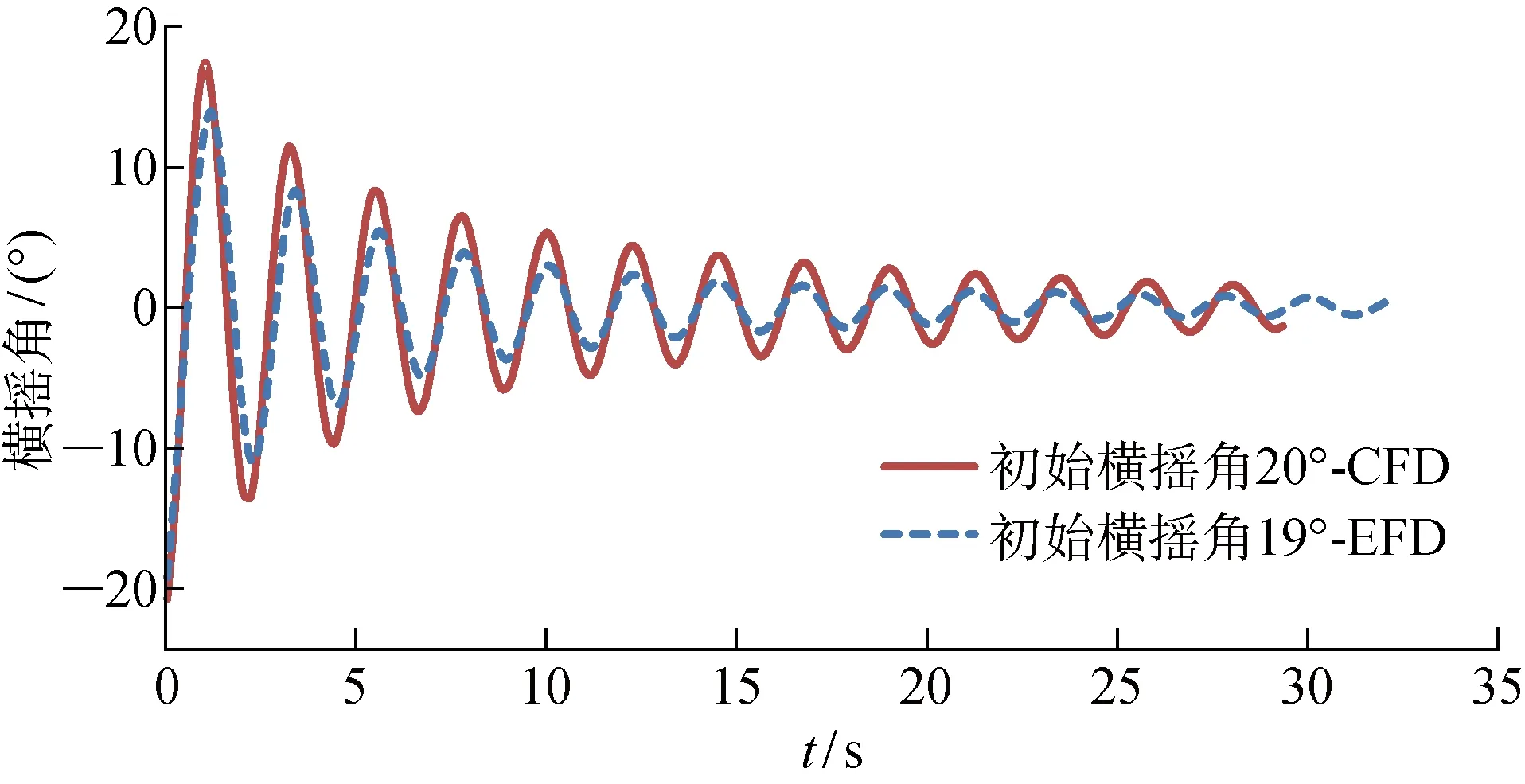
图10 完整船自由横摇衰减运动数值与试验对比图Fig.10 Comparision of numerical simulation and experiment for intact ship’s roll free-decay motion

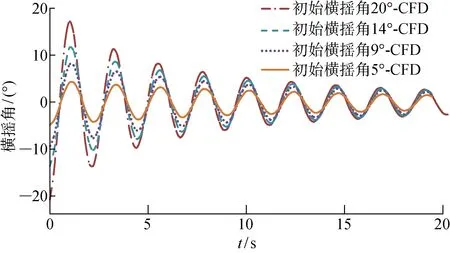
图11 完整船不同初始横摇角的自由横摇衰减运动数值对比图Fig.11 Comparision of numerical simulation intact ship’s roll free-decay motion with different initial roll angles

Tab.2Rolldampingcoefficientandnatureperiodofintactship

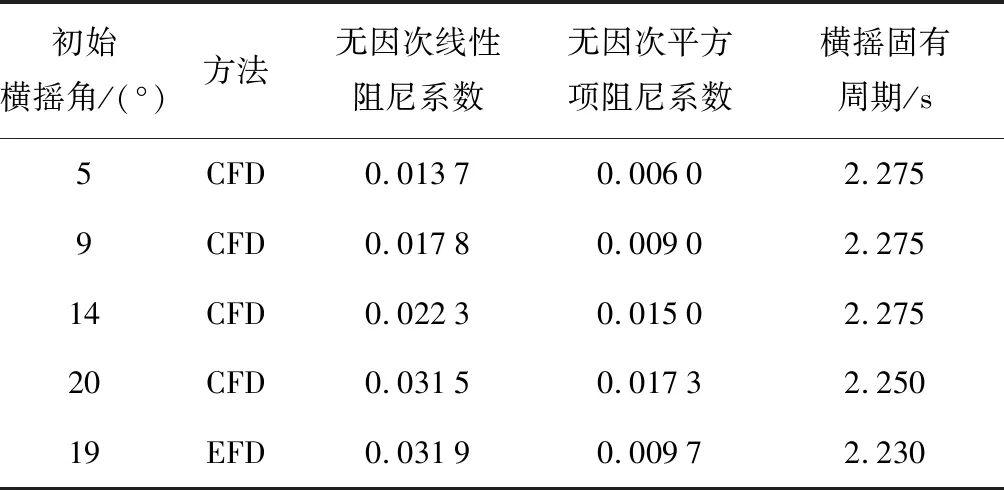
初始横摇角/(°)方法无因次线性阻尼系数无因次平方项阻尼系数横摇固有周期/s5CFD0.01370.00602.2759CFD0.01780.00902.27514CFD0.02230.01502.27520CFD0.03150.01732.25019EFD0.03190.00972.230

(2) 如图12所示，随着初始横摇角度的增大，横摇阻尼的非线性成分也在不断地增大，在初始横摇角度达到15° 及以上的时候，阻尼的非线性不可忽略.因此，在横摇运动理论预报时宜采用非线性阻尼模型，横摇的线性阻尼模型只在小角度的情况下才适用.

(3) 从图13和14(图中p′为船体表面压力)中可以看出，在舭龙骨附加阻尼的作用下，船舶的自由衰减速度相比光体船舶更快，同时船舶横摇固有周期有所增加，可以明显看到船体舭部产生较大的涡，与实际吻合，体现了CFD方法将舭龙骨等附体一体化计算对横摇阻尼的研究的重要性和必要性.

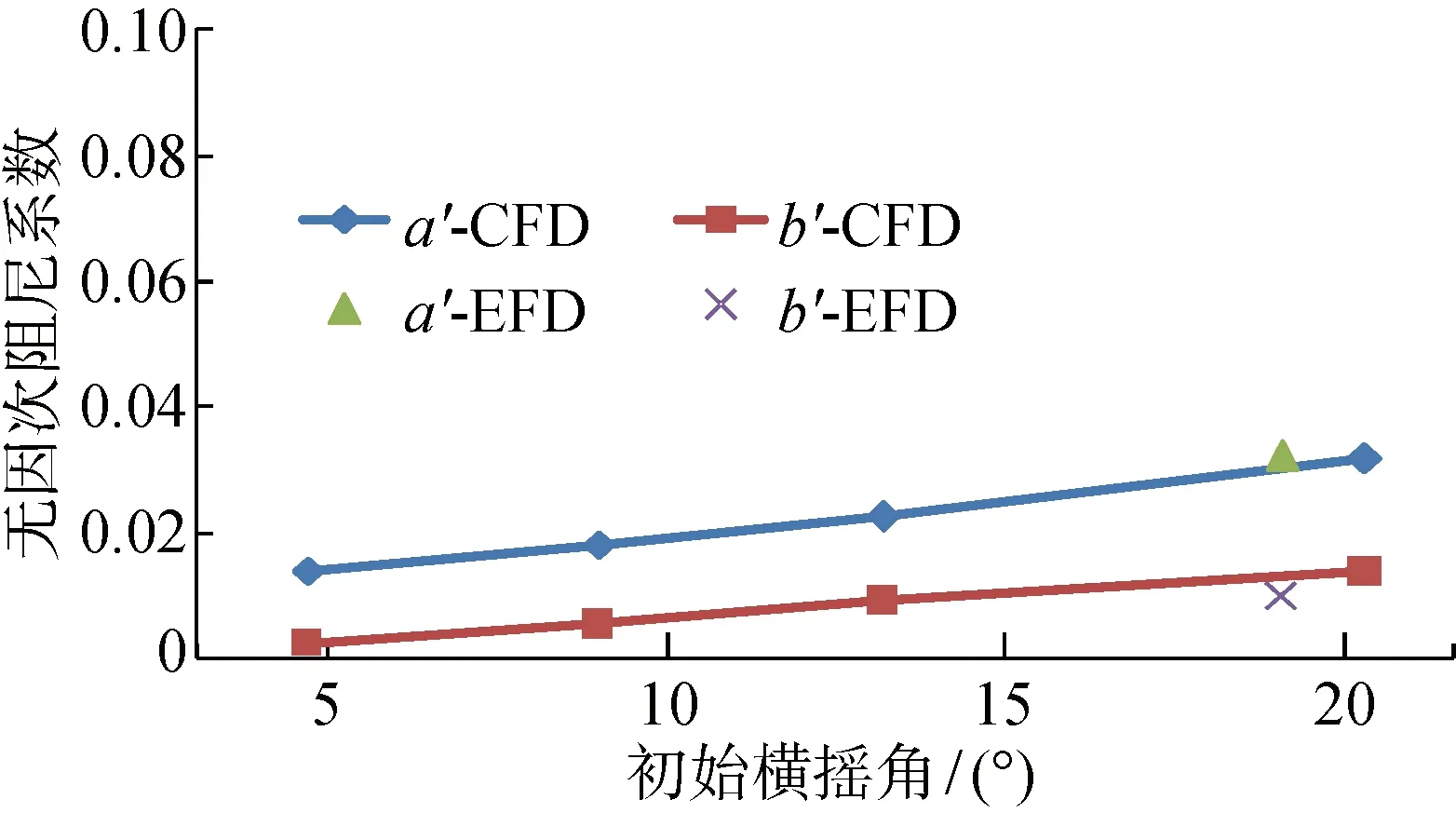
图12 不同初始横摇角下完整船舶线性与非线性横摇阻尼系数变化Fig.12 Comparision of numerical simulation and experiment for intact ship’s roll damping coefficients

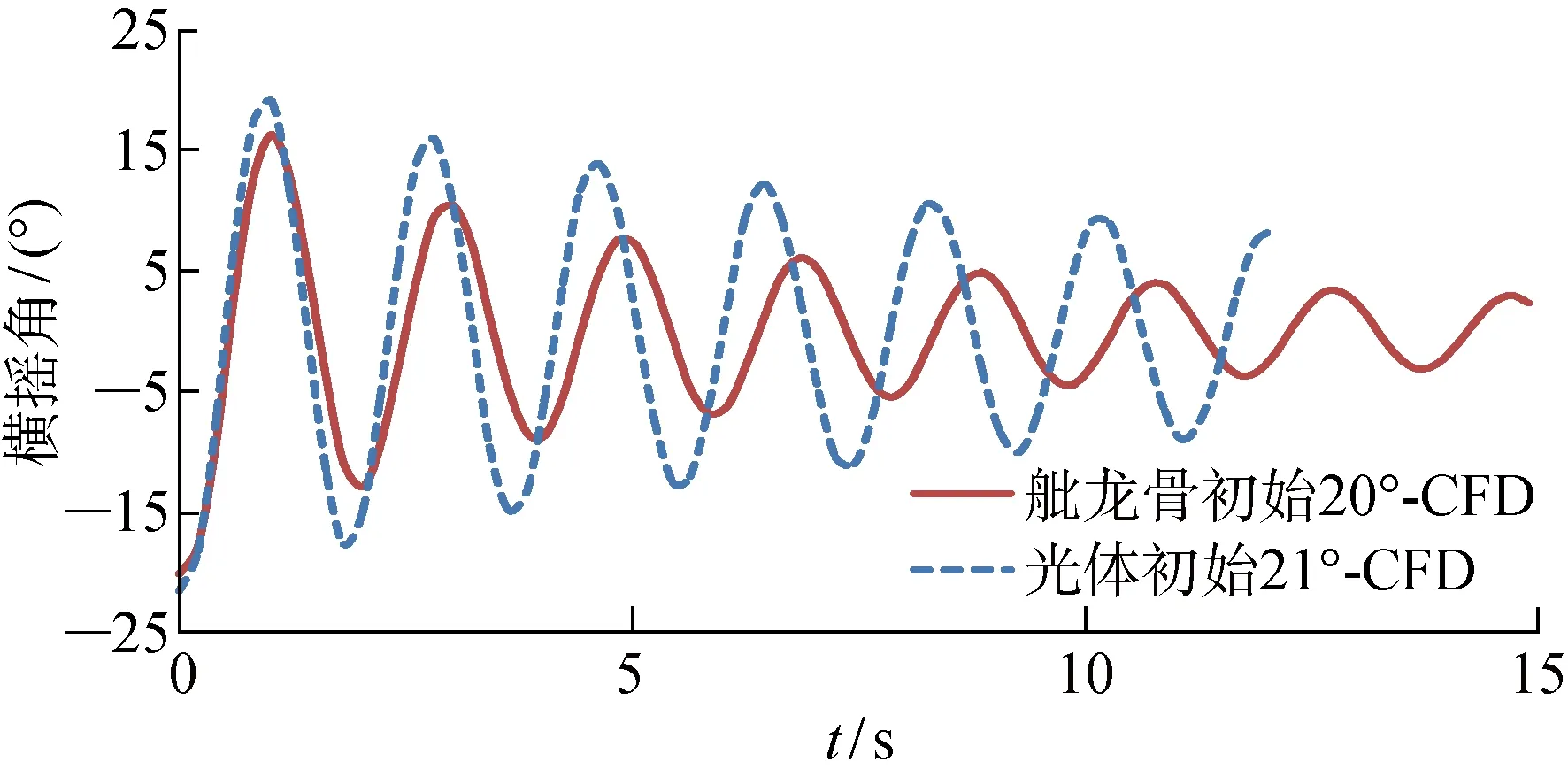
图13 带舭龙骨及光体船舶自由横摇衰减运动数值对比图Fig.13 Comparision of numerical simulation for the roll free-decay motion of intact ship with and without bilge keel

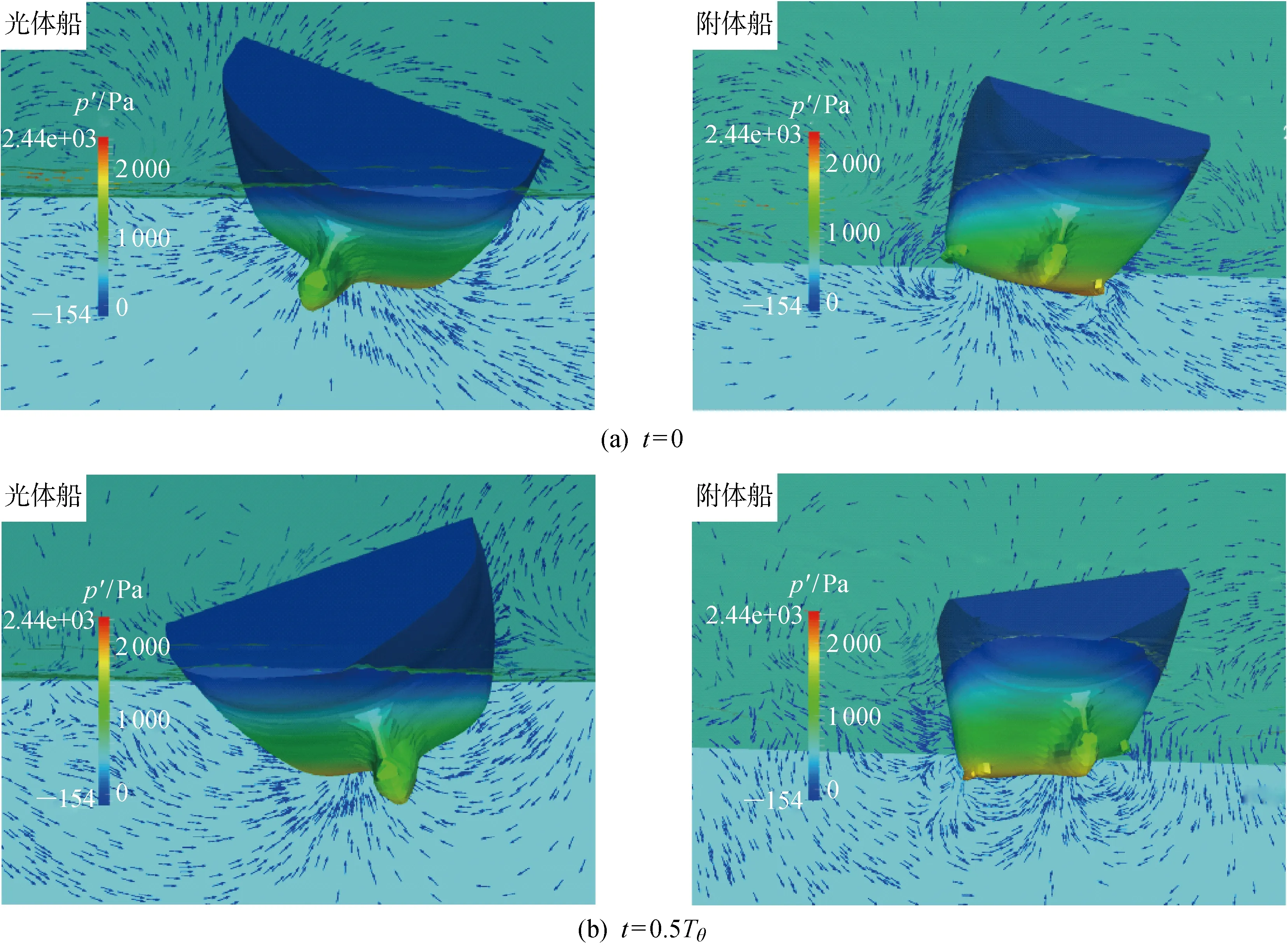
图14 完整船舶重心位置处横截面速度矢量图(初始横摇角20°)Fig.14 Velocity vector gragh at the cross section of intact ship’s gravity(initial roll angle is 20°)

2.2 第二类破损船静水自由横摇衰减数值模拟

在对完整船的自由横摇衰减模拟完成的基础上，应用OpenFOAM对第二类破损船舶的自由横摇衰减运动进行模拟，探讨横摇阻尼的变化规律.通过设置不同初始横摇角，得到不同横摇时历，由于此处破损属于不对称破损，所以自由横摇衰减曲线偏离平衡位置，如图15所示.横摇阻尼系数和周期汇总结果如表3所示，从中得到如下结论：

图15 不同初始横摇角的第二类破损船舶自由横摇衰减运动数值对比图Fig.15 Comparision of roll angle calculated by CFD method for the second situation of damage

Tab.3Rolldampingcoefficientandnatureperiodofthesecondsituationofdamage

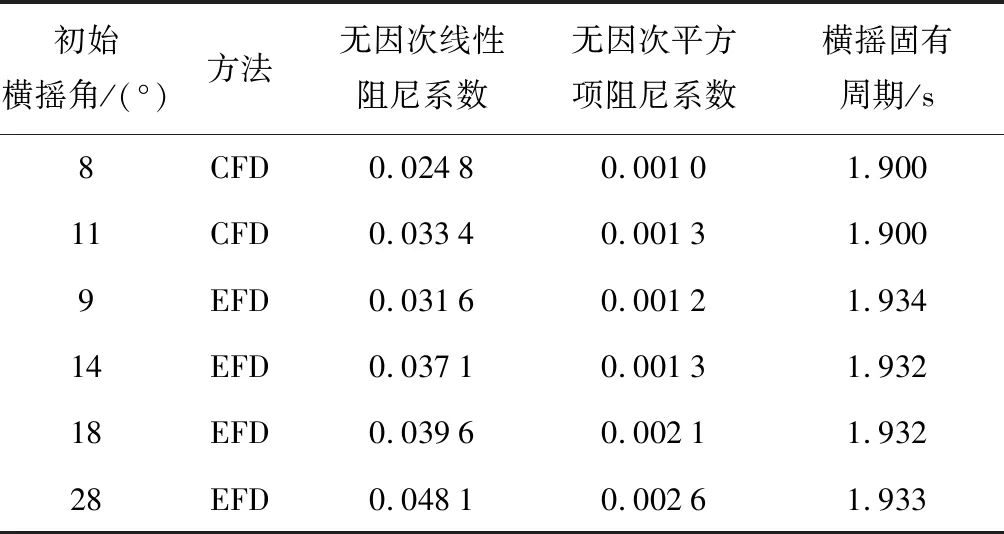
初始横摇角/(°)方法无因次线性阻尼系数无因次平方项阻尼系数横摇固有周期/s8CFD0.02480.00101.90011CFD0.03340.00131.9009EFD0.03160.00121.93414EFD0.03710.00131.93218EFD0.03960.00211.93228EFD0.04810.00261.933

(1) 将阻尼系数数值结果与试验结果进行比较，得出数值结果与试验结果比较接近，体现出阻尼的增长特性，随着初始横摇角的增加，线性和非线性阻尼系数均有所增加，如图16所示.

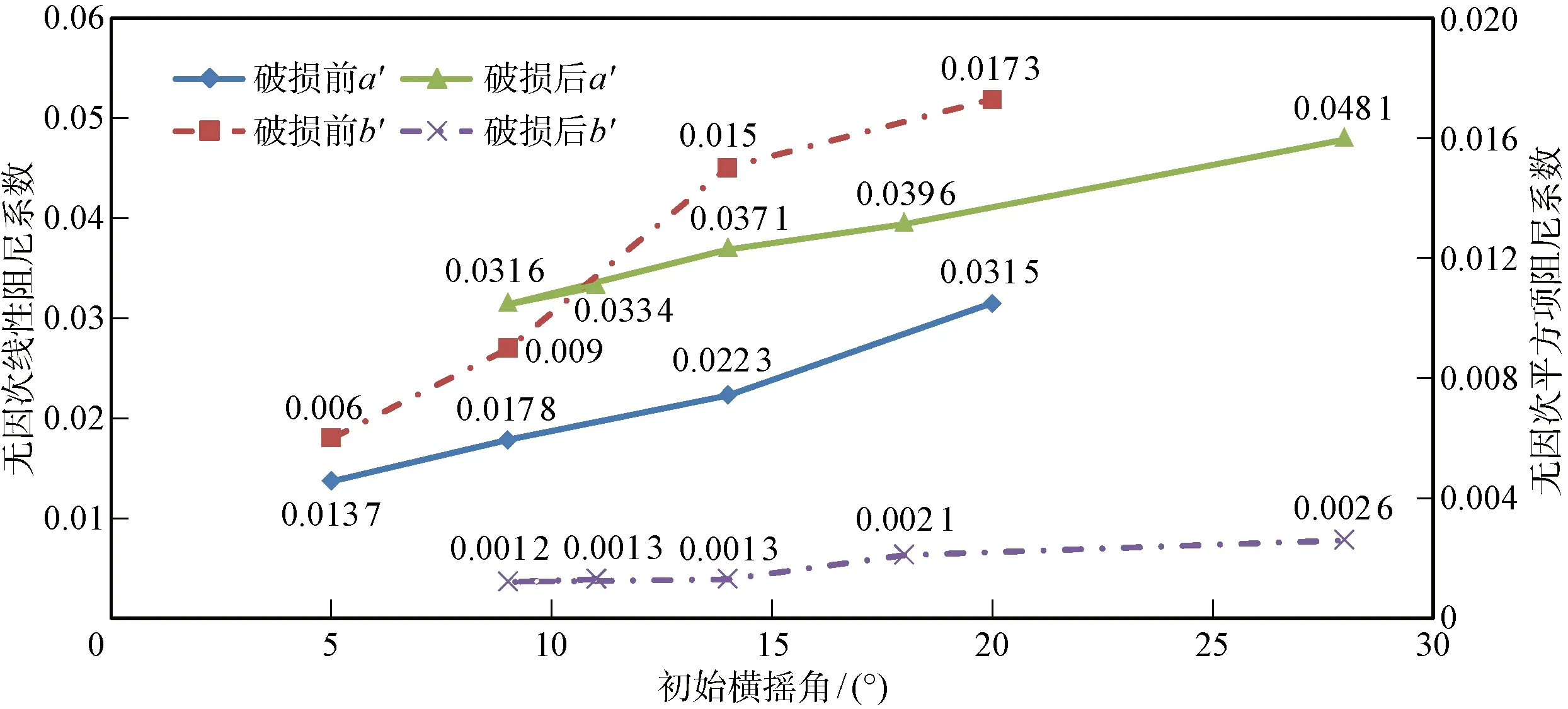
图17 破损前后横摇阻尼系数变化Fig.17 Comparision of damping coefficients between intact ship and the second situation of dmage ship

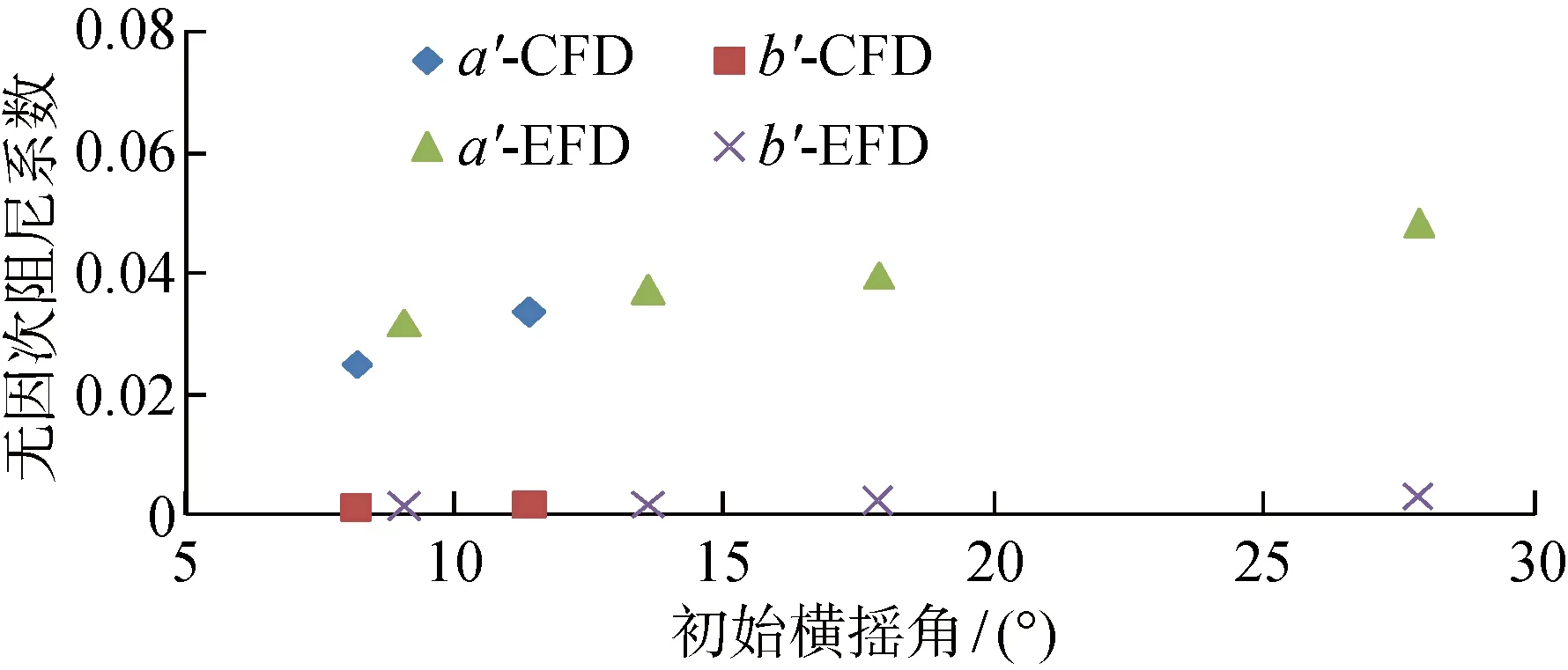
图16 不同初始横摇角下第二类破损船舶线性与非线性横摇阻尼系数变化Fig.16 Numerical simulation of roll free-decay motion for the second situation of damage with different initial roll angles

(2) 从图17中发现将第二类破损后横摇阻尼与破损前船舶的阻尼进行比较后，一是总阻尼反而有所增加，二是非线性成份所占比例下降，线性成份增加.其原因可能是第二类破损后舱室形成减摇水舱效果，叠加了水舱阻尼.与此同时，注意到固有周期发生改变导致阻尼起明显作用的区间也相应改变，也就是说，虽然破损后舱室形成了减摇效果，但是横摇阻尼起明显作用的区间发生的变化以及不对称破损下的横摇单侧幅值增大等因素都对船舶的横摇运动产生不稳定影响.

第二类破损后船舶自由衰减运动不同时刻的流场细节如图18所示，随着时间的增加，破损一侧的流体速度矢量不再处于对称状态，体现了非对称破舱水的晃荡对船体运动的耦合影响.

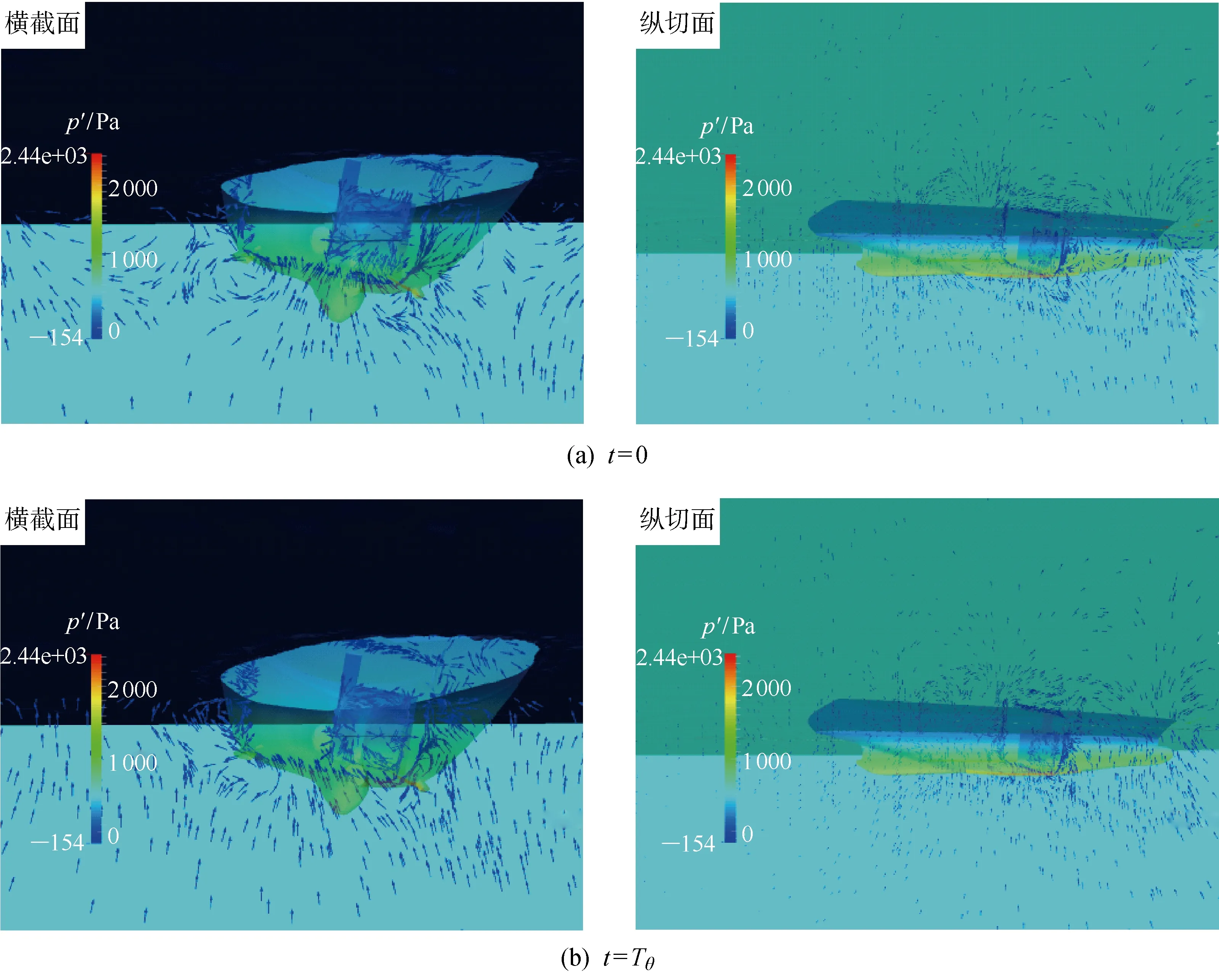
图18 第二类破损船舶重心位置处速度矢量图(初始横摇角10°)Fig.18 Velocity vector gragh at the cross section of the second situation of damaged ship’s gravity (initial roll angle is 10°)

2.3 第三类破损船静水自由横摇衰减数值模拟

对第三类破损围网渔船的自由衰减运动设置2种初始条件：一种是破损舱室初始水位与船舶吃水持平(初始条件I)；另一种是破损舱室初始水相为零(初始条件 II).这样设置的原因是：① 受试验条件限制，自由横摇衰减试验均在破损进水达到平稳后进行，无法考虑船舶破损发生时刻的动态进水过程，为了与试验比较，数值模拟设置第一种初始条件；② 为了考察破损的进水过程中舱内流场瞬时变化以及对船舶横摇运动的影响，数值模拟设置第二种初始条件.通过分析得到如下结论：

(1) 破损进水过程对整个横摇阻尼的影响并不大，线性和非线性阻尼误差均为9%左右；两种初始条件对整个横摇固有周期则几乎无影响，误差为 0.8%，如表4和图19所示.

(2) 破损进水过程对整个垂荡模态的影响较大，如图20所示，由于船舶吃水的瞬时变化造成垂荡在第一个周期内的剧烈振荡，第一个周期之后的浮态变化则与未考虑破损过程的情况趋于一致.

(3) 破损进水过程在一个周期内达到平稳，从图21可观测到进水喷涌、液面翻卷及波动等瞬时现象，并且注意到破损开口的上缘部位水流速度矢量变化剧烈， 体现了舱内进水对空气的排挤影响.

表4第三类破损横摇阻尼系数及固有周期汇总表

Tab.4Rolldampingcoefficientandnatureperiodofthethirdsituationofdamage

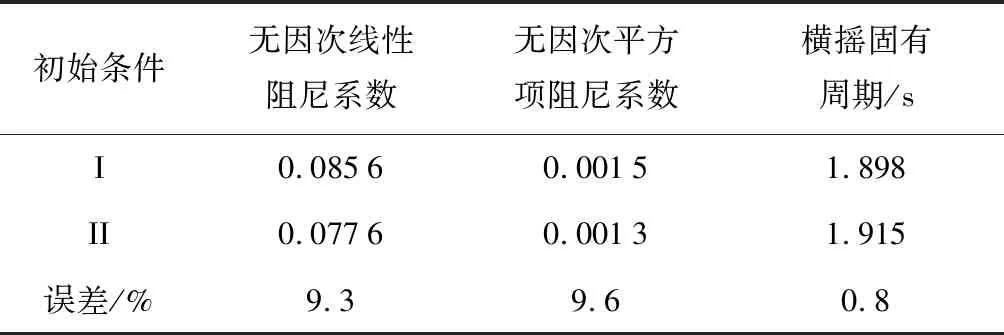
初始条件无因次线性阻尼系数无因次平方项阻尼系数横摇固有周期/sI0.08560.00151.898II0.07760.00131.915误差/%9.39.60.8

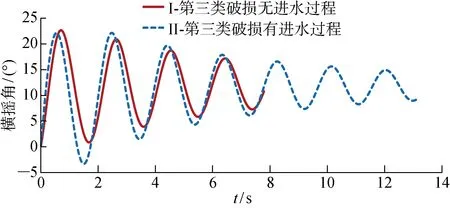
图19 有无考虑破损进水过程的横摇运动时历对比曲线Fig.19 Time history of roll motion with different initial conditions

图20 有无考虑破损进水过程的垂荡运动时历对比曲线Fig.20 Time history of heave motion with different initial conditions

图21 第三类破损船进水过程Fig.21 Dynamic process of water penetration

3 结论

运用OpenFOAM开源代码平台实现黏性流中完整和破损船舶自由横摇衰减运动模拟，探讨不同初始横摇角、不同破损形式以及破损过程对横摇阻尼的影响，并开展试验验证研究，得到如下结论：

(1) 破损船体的横摇阻尼特性比较复杂.船舶在遭遇第二类破损后，横摇阻尼较完整船舶阻尼有所增加，其中非线性成份所占比例下降，线性成份增加.第三类破损与第二类破损相比，船舶横摇阻尼也有所增大.破损发生后，船舶的横摇固有周期也会发生改变，但是破损形式对横摇固有周期影响不大.

(2) 分析第三类破损船舶的破损进水过程发现，是否考虑船舶达到稳态前的破损过程对整个横摇阻尼的影响并不大；对整个横摇周期则几乎无影响；但是，对整个垂荡模态的影响较大，由于船舶吃水的突变造成垂荡在第一个周期内的剧烈振荡，第一个周期之后则与未考虑破损过程的情况趋于一致.因此，在研究船舶横摇阻尼的问题上，破损过程在一定程度上可以简化处理.

(3) 从方法上尝试应用OpenFOAM纯黏性代码对破损船舶在波浪中的流固耦合以及舱内外水耦合等难点问题进行研究，实现了CFD预报完整船、破损开口船以及带自由液面船舶黏性横摇阻尼的工程应用，为进一步处理波浪中破损船舶的瘫船稳性问题研究奠定基础，也为IMO进行破损稳性的新一代衡准研究提供参考.

(4) 船舶静水中的自由横摇衰减运动得到的阻尼仅为共振频率处的阻尼，未来将进一步考虑波浪中的自由横摇衰减运动，研究不同波浪频率下的船舶阻尼.