基于区间值直觉模糊集加权TOPSIS的高校教师教学效果评价

黄淑伟, 张燕丽

(沈阳师范大学 科信软件学院, 沈阳 110034)

0 引 言

多属性决策就是从有限个可供选择的方案中,依据一定的评选准则,选取一个最优方案的问题。选择最优方案的评价方法多种多样,如最简单的AHP法,TOPSIS(Technique for Order Preference by Similarity to Ideal Solution,逼近理想解排序)法,二者混合的方法[1],统计分析方法[2]等。然而,随着不断增长的问题复杂性以及人们对某些问题认识的模糊性,使得在有些情况下,获取的各属性值判断结果为一个区间数[3],直觉模糊数[4],区间值直觉模糊数[5-8]等多种形式,因而提出了模糊环境下的多种多属性决策方法。文献[9-11]是基于TOPSIS方法提出的模糊多属性决策问题。文献[12]使用区间值直觉模糊集犹豫度的概念,定义得分函数和精确函数,并据此提出基于理想点法的区间值直觉模糊集多属性决策方法。文献[13]使用区间值直觉模糊集定义,定义了2个区间值直觉模糊集的接近系数,通过计算备选方案到区间值直觉模糊正理想解和负理想解的距离来确定接近系数,从而判断备选方案的优劣次序。本文把区间值直觉模糊定义与TOPSIS相结合,提出一种基于区间值直觉模糊集加权TOPSIS法,并利用此方法对教师教学效果进行评价。

1 相关概念

定义1[14]设X是非空集合,X上的直觉模糊集A定义为一个三元组:

A={〈x,uA(x),vA(x)〉|x∈X}

其中:uA:X→[0,1]和vA:X→[0,1]均为X上的隶属函数,且0≤uA(x)+vA(x)≤1,其中:uA(X),vA(x)分别是X上元素x属于集合A的隶属度和非隶属度,表示支持元素和反对元素的解释值下界。πA(x)=1-uA(x)-vA(x)≥0,表示元素x属于X的犹豫度,显然,0≤πA(x)≤1。

由于客观事物的复杂性和人类认识问题的不确定性,表示支持和反对的描述难以用精确的实数值来表示,而采用区间数形式则较好地解决了这一问题。因此,Atanassov等对直觉模糊集进行了拓展,提出了区间值直觉模糊集的概念。

定义2[15]设X是非空集合,X上的区间值直觉模糊集A定义为一个三元组:

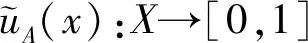
对于X上的每一个区间值直觉模糊集,其犹豫度πA(x)的下界和上界为:[πA(x)]L和[πA(x)]U,其中:

定义3[13]2个区间值直觉模糊集A、B的欧氏距离dIVIFS(A,B)定义为:

其中:[d(A,B)]L,[d(A,B)]U分别为距离的下、上界。

2 基于区间值直觉模糊集的多属性决策

2.1 区间值直觉模糊多属性决策问题描述

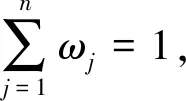
2.2 确定区间值直觉模糊集的正理想解和负理想解

所谓区间值直觉模糊集的正、负理想解,即为所有方案中各项属性达到最理想状态的最优方案和都表现出最劣值的最差方案。

设区间值直觉模糊集的正理想解A+和负理想解A-分别为

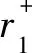
正理想解

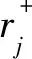
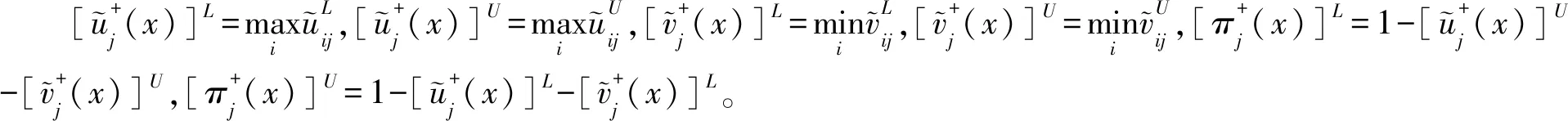
负理想解

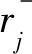
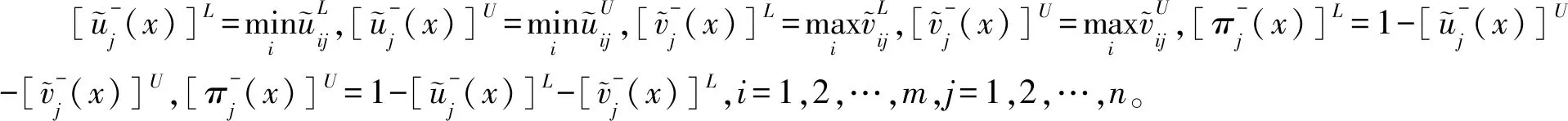
2.3 计算各备选方案ai到正理想解A+和负理想解A-的距离

若不考虑属性集U=(u1,u2,…,un)各属性上的权重值,备选方案ai到正理想解A+距离为dIVIFS(ai,A+),其下、上界分别为[d(ai,A+)]L和[d(ai,A+)]U。

备选方案ai到负理想解A-距离为dIVIFS(ai,A-),其下、上界分别为[d(ai,A-)]L和[d(ai,A-)]U。

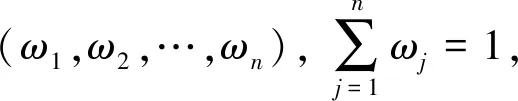
备选方案ai到负理想解的距离为:

2.4 计算各备选方案ai的综合评价值

其综合评价值表示各备选方案ai与正、负理想解的距离进行比较,距离正理想解越近和距离负理想解越远的方案,其紧密度的综合评价值ri越大,即方案越优,反之则方案越劣,因此,按其综合评价值ri的大小可实现对方案优劣的排序。

3 高校教师教学效果评价实证

本文对高校教师教学效果评价指标引用了文献[15]中给出的高校教师教学效果满意度5项评价指标:教学方法、教学内容、教学态度、作业布置和教师整体形象,作为区间值直觉模糊集评价属性集U。以某高校某班级80名学生为调查对象,将班级学生按人数随机分成4组,分别对给该班任课的3位教师(3个方案)教学效果进行投票。投票采取满意、不满意和放弃回答3种情况,对调查结果进行整理计算,确定4个组对3位教师教学效果的满意和不满意情况的比例值,分别定义为对高校教师教学效果评价的满意值上下界和不满意值上下界。利用区间值直觉模糊集加权TOPSIS法实现对教师教学效果的评价。其中5项指标:教学方法、教学内容、教学态度、作业布置和教师整体形象的权值分别为:0.4,0.3,0.1,0.1,0.1。各教师教学效果评价的区间值直觉模糊集决策矩阵如表1所示。

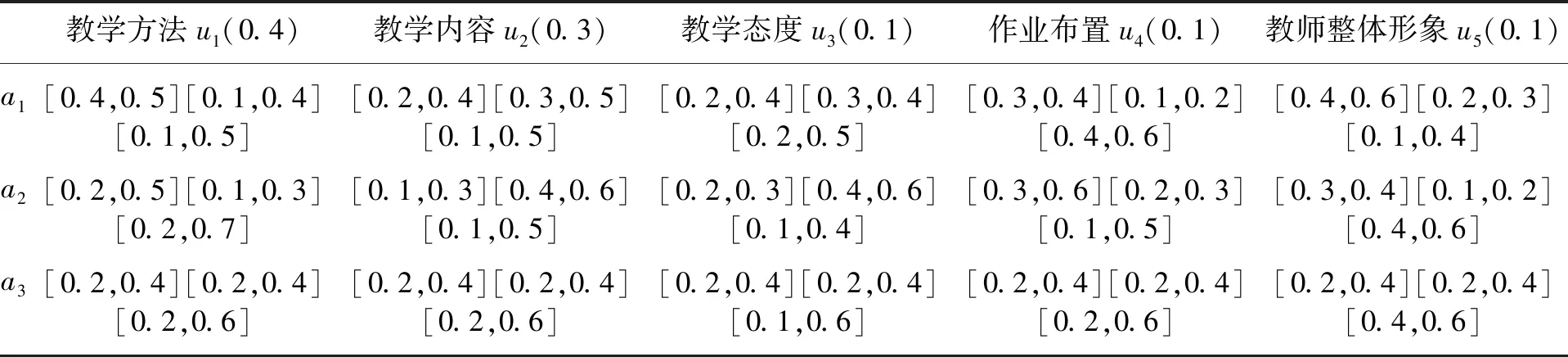
表1 教师教学效果评价的区间值直觉模糊集决策矩阵Tab.1 Decision matrix of teaching effectiveness evaluation based on interval-value intuition fuzzy sets

由决策矩阵表1可知正、负理想解A+和A-,如表2所示。

表2 教师教学效果区间值直觉模糊集的正理想解和负理想解

计算各方案ai与正、负理想解的加权距离和紧密度的综合评价值ri,如表3所示。

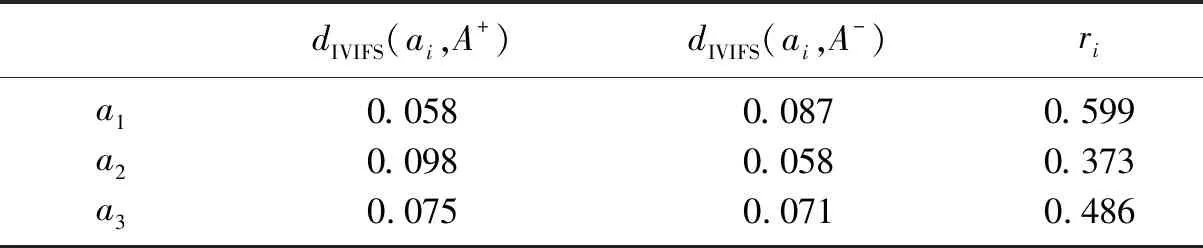
表3 教师教学效果评价的计算结果Tab.3 Results of teaching effectiveness evaluation

根据各方案的综合评价值ri大小,方案的优劣次序为:a1,a3,a2。所以教师a1教学效果为最佳,这一结论也与实际情况相吻合。

4 结 语

区间值直觉模糊集对于多属性决策问题中属性评价值不确定或信息不确定的问题,提出了一种新的解决方案,在处理模糊问题时表现的更灵活。与TOPSIS结合,用于研究模糊环境下的多属性决策问题更有效,教学效果评价实例也进一步证明了其优势。