基于动态博弈模型的有机农产品动态定价及其稳定性

李 文, 温明振, 温 蔷

(1. 辽宁大学 经济学院, 沈阳 110036; 2. 辽宁大学 商学院, 沈阳 110036;3. 盖州市农业技术推广中心, 辽宁 盖州 115200)

0 引 言

改革开放40年,我国经济取得了举世瞩目的成就,人民生活水平发生了翻天覆地的变化。近年来,随着“地沟油”“瘦肉精”等食品安全问题的曝光,大众对食品安全愈发关注,越来越多的消费者追求绿色食品,这为有机农产品的推广提供了良好的宏观环境。有机农产品是指在生产中不采用基因工程技术,不使用化学合成物,遵循自然规律和生态学原理生产出来的农产品[1]。由于有机农产品对生产工艺有较高的要求,其生产成本高于传统农产品,因此有机农产品在我国农产品消费市场的普及率较低,与发达国家存在一定的差距[2]。虽然有机农产品绿色、安全的概念深入人心,但是受高昂售价的影响,很多消费者仍会选择较低价格的传统农产品。受价格因素的制约,消费者对有机农产品的接受度大相径庭,市场中存在2类消费群体,一类对有机农产品认可度较高,成为其忠实购买者,另一类则会选择“性价比”更高的传统农产品。现实中,我国有机农产品市场仍有广阔的发展空间,因此,如何针对消费群体的消费特性[3],对有机农产品进行合理定价,有利于生产厂商的利润最大化,同时对有机农产品市场的开阔、有机农业的稳定、持续发展也有着重要的影响。现有文献对农产品定价问题进行了一些研究,如李琳等[4]针对生鲜农产品的易损耗性研究了单周期零售商最优定价;王磊等[5]基于生鲜农产品变质特性和消费者偏好,通过构建时变模型,研究了零售商最优定价策略;此外,宁威[6]、王冲等[7]利用期权模型对农产品定价决策进行了研究。目前,诸多学者对传统农产品的定价问题展开了相关研究,却鲜少将有机农产品和传统农产品作为研究对象进行动态定价的系统研究。因此,本文基于博弈和复杂系统模型,分析有机农产品和传统农产品定价博弈行为,进而得出农产品厂商最优定价策略。

1 静态博弈模型

(1)

2种农产品的销售利润可以表示为:π=(p-c)Q。即单位产品售价与成本的差值与销量的乘积。于是2种农产品的利润为:

(2)

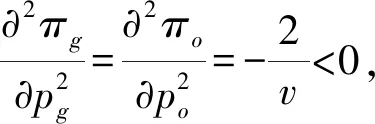
(3)

将求得的均衡价格带入到利润模型中可以求得传统农产品和有机农产品的均衡销量为:

(4)

从均衡销售量可以看出,2种农产品的销量只与单位成本有关系。其中,传统农产品销量仅取决于自身的单位成本,而有机农产品的销量同时受2种产品单位成本的影响,随着有机农产品成本的增加而减少,随着传统农产品成本的增加而上升。

由此,传统农产品和有机农产品的均衡利润可以表示为:

(5)

根据公式(5),传统农产品的成本提高会使得其利润不降反升,而有机农产品成本的降低会带来利润的提高。因此对于有机农产品生产者,需要面对降低成本的问题。成本的降低不但提升自身的收益,还能提高粮食销售量,进而提高有机农产品的市场份额。

2 动态博弈模型

本文前一部分,考虑了在静态博弈的情况下,传统农产品和有机农产品的博弈情况,得出了博弈的均衡价格,进而得出了均衡销量和利润。然而,不管是传统农产品还是有机农产品,其定价都是在每一个销售周期的期初,而购买过程都是发生在定价之后,因此,作为决策者,农产品厂商并不能根据当期的情况做出最优的价格决策。农产品厂商是有限理性的,只能根据以往的销售情况对销售价格进行动态的调整,不断实现更高的利润,最终达到最高的利润。动态博弈的规则有很多,比如有限理性规则、自适应规则、天真预期规则等,本文假定厂商是有限理性的,采用的调整规则为:

(6)

该动态调整是根据价格对利润的边际贡献来确定对价格的调整方向。上文已经证实,厂商的利润是关于价格的凹函数,因此当价格的边际利润为正数时,继续提高价格会增加利润;当价格的边际利润为负数时,降低价格会增加利润。调整的终点是价格的边际利润为零。式(6)中价格的调整方向,正是符合该调整规则。式中,参数αi表示每一期对价格调整的速度。于是,本文中的动态博弈模型可以看作一个离散动力系统:

(7)

在动力系统(7)达到均衡状态时,每一期的价格将处于均衡状态,即pi(t+1)=pi(t)。在这个条件下,可以求出4个均衡解。以Ei(pg,po)表示,分别为:

(8)

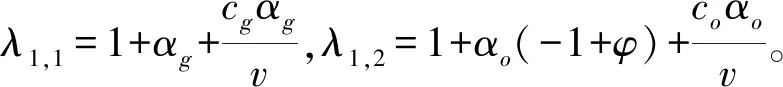
(9)

图1 系统(7)的稳定域Fig.1 The stability domain of system(7)

在其他很多研究混沌系统的文献中,决策变量调整速度对系统的影响会相互影响对方。然而在本文的模型中,决策变量调整速度对系统的稳定性只与一些确定性的参数有关,与调整速度参数彼此无关。

通过数值模拟,可以更加直观和清晰地表现出系统的动态特性。根据上文对各个参数的定义和范围的规则,可以做出如下的数值模拟:v=4,φ=2,cg=0.5,co=1。进而,绘制满足条件(9)的稳定性区域,如图1所示。

图2 参数αg变化下系统的分岔图和最大Lyapunov指数图Fig.2 Bifurcation diagram of the system with variable parameters αg and maximum Lyapunov exponent garph

稳定域显示,当变量调整速度处于较低水平时,系统可以处于稳定状态。而当参数αg>1.951或者αo>1.260时,系统将失去稳定。从系统稳定性条件(9)和图1显示的稳定域可以看出,变量调整速度不会相互影响稳定性条件,于是可以限定αo=0.1,观察参数αg的变化产生的系统分岔图,如图 2所示。

随着参数αg的提高,系统从稳定状态进入2倍周期分岔状态,进而进入4倍、8倍周期分岔,最终进入混沌状态。在混沌状态下,农产品厂商无法得到一个稳定的均衡决策价格,进而也就无法得到一个均衡的利润。在动态博弈过程中,混沌状态是决策者需要考虑的。虽然提高调整速度αg和αo的数值可以使得厂商在较短的时间内达到最优状态,但是过大的决策变量调整速度会使得系统失去稳定状态。农产品的价格受产量的影响非常显著。可替代农产品(传统农产品和有机农产品)之间价格的变化诱导农产品种植种类和数量的变化。当市场上有机农产品价格显著提高的时候,农户会大量转向有机农产品的种植,出现产品供大于求,致使产品价格下跌。 所以在市场中会存在谷贱伤农的现象。因此,对于有机农产品价格的调整要循序渐进,不可过快,否则会因为价格出现周期性的波动而使得农产品的产量出现相应的波动。如图2所示,当调整参数αg处于1.95～2.395之间变化时,农产品的价格和产量会呈现周期性变化,会在2个值之间波动。本文给出了系统进入混沌状态的临界条件,如条件(9),根据不同参数条件,厂商可以计算出决策变量调整速度的上限值。在不同的参数条件下,系统的稳定性临界值,均衡价格以及均衡利润可以用表1表示。

表1 不同参数下均衡状态和系统稳定的临界条件Tab.1 Critical conditions for equilibrium state and system stability under different parameters

通过表 1可以看出当参数在合理范围内变化时,决策变量和厂商的销量、利润等指标的变化情况。进一步,还可以计算出保持系统稳定的决策变量调整速度的上限,这有助于指导决策者在避免系统进入混沌状态的前提下,以最快的速度进行决策变量的调整,以求最快达到动态博弈的均衡状态。

3 结 语

基于消费者对传统农产品和有机农产品不同的偏好,本文主要分析了在静态博弈和动态博弈2种情形下,有机农产品和传统农产品的定价问题。在动态定价博弈情形下,系统可能发生的混沌状态,本文运用复杂系统理论分析方法,求出了保持系统稳定性的条件。本文研究有助于有机农产品厂商通过进行成本控制提高效益,并通过控制决策变量调整速度,在保持系统稳定的前提下,以最快的速度达到均衡状态,获得更高的收益。