一种模糊时间序列分析方法

马 芳, 王鸿绪

(1. 辽宁大学 经济学院, 沈阳 110036; 2. 海南热带海洋学院 海商学院, 海南 三亚 572022)

在过去几十年中,时间序列预测模型是人们最常用的预测模型之一[1]。1993年Song和Chissom[2-4]首次提出模糊时间序列预测模型,把时间序列作为模糊系统[5]进行研究,并首次研究阿拉巴马大学1971—1992年的注册数问题。文献[6-7] 应用提出的模糊时间序列预测模型,研究同样问题,获得2007年来最高的预测精确度[7],受到许多学者的青睐,许多预测模型因此而创立[8-13]。

1 模糊时间序列分析方法(AMFTS)的基本理论

定义1 设时间序列论域为M= {M1,M2,…,Mn}。历史数据的比的计算公式为

Jg-1=Mg/Mg-1

(1)

得到历史数据的比的论域为J={J1,J2,…,Jn-1}。

定义2 设时间序列论域为M={M1,M2,…,Mn},历史数据的比的论域为J={J1,J2,…,Jn-1}。则可以定义

(3)

其中:自变量q∈(0, 1];s∈(0, 1];x∈(0, 1]。Kj(q,s,x)称做AMFTS(或时间序列)的q年预测函数,或预测公式,或预测模型。

定义3 设时间序列论域为M={M1,M2,…,Mn},历史数据的比的论域为J={J1,J2,…,Jn-1}。能够建立AMFTS的j年的预测模型Kg(q,s,x)。当遍取g∈{1,2,…,n},并且遍取自变量q∈(0, 1],s∈(0, 1],x∈(0, 1]时,能够建立AMFTS的无穷多个预测模型Kg(q,s,x)。时间序列M的所有预测模型Kg(q,s,x)的全体叫做一种模糊时间序列分析方法。其中任意一个元素Kg(q,s,x)叫做时间序列M的g年预测模型。

定理1 设时间序列论域为M={M1,M2,…,Mn},历史数据的比的论域为J={J1,J2,…,Jn-1}。对任意取定的q∈(0, 1],s∈(0, 1],x∈(0, 1]。固定s,当q→0,x→0时,则AMFTS的预测函数Kg(q,s,x)收敛,并且q年AMFTS的预测函数Kg(q,s,x)收敛于q年时间序列M中的元素Mg(g=1, 2,…,n)。

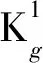
2 数值实验和结果分析

实验为了验证所提出的AMFTS中的分析方法的有效性,以阿拉巴马大学1971—1992年的注册数[3]作为样本数据(表1),进行比较研究。

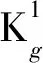
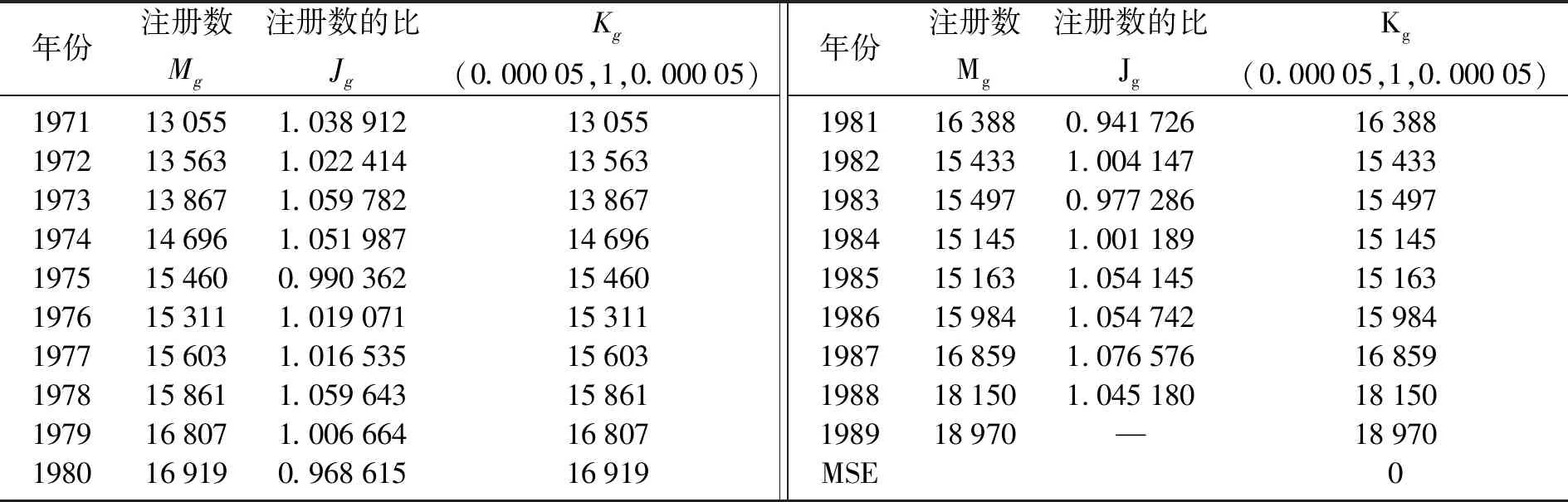
表1 应用建模FMKg(0.000 05,1,0.000 05)仿真预测阿拉巴马大学1971—1989年的注册数

注: 在本文中,均方误差(Mean square error,MSE):MSE=(Mg-Kg)2。

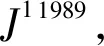
第2轮尝试计算 数据见表2,略。

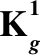
表2 应用建模FM(0.000 05,1,0.000 05)预测阿拉巴马大学1990—1992年的注册数

本文依据为“当MSE比较大时,应该减少注册数的比J1982;MSE越大,注册数的比J1982减少的幅度越多;当MSE比较小时,应该增加注册数的比J1982;MSE越小,注册数的比J1982的增加的幅度越多”,这是模糊控制的规则的语言叙述[14]。

3 与改进的人工鱼群算法-模糊时间序列预测模型的比较

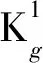
表3 各模型仿真阿拉巴马大学1971—1989年的注册数的比较Tab.3 The model simulates the number of registrations of the university of Alabama from 1971 to 1989 are compared

4 结 语

本文提出一种模糊时间序列分析方法,通过仿真预测阿拉巴马大学1971—1989年的注册数和预测未来的1990—1992年的注册数的比较研究,显示出AMFTS的建模FMK比FGAFS-FTS更具优势,验证了所提方法的良好效果。