摭谈类比思想在高中数学教学中的运用实践

☉江苏省泰州中学 周花香

类比思想方法是数学思想方法的一种，高中数学新课程标准明确指出，类比思想方法的运用是培养学生创新思维的重要途径之一，是形成创新思维的基础；实践表明，在高中数学教学中灵活地运用类比思想，有助于学生深刻理解数学新知，有助于学生形成解决数学问题的思路，有助于学生获得知识类比迁移的能力.众所周知，数学问题中类比方法主要运用于类似形式、性质、解题方法等方面，在高中数学的圆锥曲线部分，圆、椭圆、双曲线之间存在很多相似性.多数教师用来体现类比思想方法的巧妙性的极佳素材.笔者根据教学实践，借助圆、椭圆、双曲线三种圆锥曲线为探究载体，从“定值、定点、定轨迹”三个角度进行类比，旨在抛砖引玉，仅供教育同仁参考，不当之处，敬请批评指正.

一、类比思想与定值问题的“接触”

圆的性质1：已知A，B为⊙O上任意两点，且满足OA⊥OB，则S△OAB为定值.

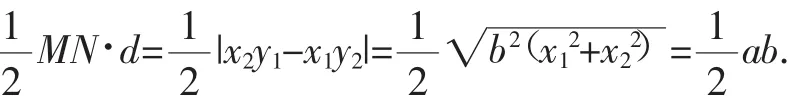
二、类比思想与定点问题的“碰撞”

圆的性质2：已知点P为⊙O上任意一点，过点P作圆的两条直线分别交圆于点M和N，且满足MP⊥NP，则MN过某一定点.

三、类比思想与定轨迹问题的“共舞”

圆的性质3：已知在⊙O：x2+y2=r2外存在一动点P，过P点作⊙O的切线PM，PN（M，N为切点），且满足PM⊥PN，则动点P的轨迹方程为x2+y2=2r2.

椭圆与圆类比：已知A（x0，y0）为椭圆0）外一动点，AE，AF是椭圆的两条切线，且AE⊥AF，则动点A的轨迹方程为x2+y2=a2+b2.

证明：若直线AE和AF中有一条直线平行于y轴（斜率不存在），则动点A的坐标为（a，b）.若直线AE和AF都不平行于y轴，令过A点的直线方程为y=kx+m，代入椭圆方程，得（a2k2+b2）x2+2a2kmx+a2m2-a2b2=0.令Δ=0，即b2+a2k2=m2，根据题意，点A在直线y=kx+m上，即y0=kx0+m，则（y0-kx）02=b2+a2k2，化简此式，可得（x02-a2）k2-2x0y0k+y02-b2=0，根据韦达定理，可知由题意知过A点的两条切线AE⊥AF，即k1k2=-1，则x2+y2=a2+b2.双曲线与椭圆类比：已知A（x0，y0）为双曲线外一动点，AE，AF是双曲线的两条切线，且AE⊥AF，则动点A的轨迹方程为x2+y2=a2-b2.

证明：根据题意，直线AE和AF都不平行于y轴，令过A点的直线方程为y=kx+m，代入双曲线方程，得（b2-a2k2）x2-2a2kmx-a2m2-a2b2=0.令Δ=0.即a2k2-b2=m2，根据题意，点A在直线y=kx+m上，即y0=kx0+m，则（y0-kx0）2=a2k2-b2，化简此式，可得（x02-a2）k2-2x0y0k+y02+b2=0.根据韦达定理，可知由题意知过A点的两条切线AE⊥AF，即k1k2=-1，则x2+y2=a2-b2.

圆的性质4：已知A（x0，y0）为圆⊙O：x2+y2=r2上一个固定点，过点A作圆的任意两条弦AE和AF，且AE⊥AF，过A点作AD⊥EF于D点，则垂足D的轨迹方程为，即（x-x0）x+（y-y0）y=0.

椭圆与圆类比：已知A（x0，y0）为椭圆b＞0）上一个固定点，过点A作椭圆的任意两条弦AE和AF，且AE⊥AF，过A点作AD⊥EF于D点，则垂足D的轨迹

四、结束语

在高中数学教学中，类比思想方法的灵活运用有助于学生链接数学新知识和旧知识，构建知识网络体系；学生在数学类比探究的过程中不断体验数学知识、数学概念的形成过程，在自主探究的学习过程中感悟运用数学类比思想方法处理实际问题的优越性与实效性.实践表明，类比思想方法是数学解题教学中常用的解题方法之一，作为一线高中数学教师，在平时的数学教学活动中，应该积极创造条件，引导学生进行类比思想方法的有效运用，培养学生提出问题、分析问题和解决问题的能力，培养学生的创造性思维能力，促进学生数学学科核心素养的提升.W