数学模型搭舞台，数形共奏“核心素养”曲——三角函数y=Asin（ωx+φ）的图像变换的教学尝试

☉广东省广州市花都区第二中学 张伟文

三角函数y=Asin（ωx+φ）的图像变换一直以来都是教学的重点与难点，尤其是三角函数既涉及横向伸缩变换，又涉及横向平移变换的时候，到底该“平移多少个单位”的问题往往令学生困惑不已，屡做屡错.对于这一难点的突破，广大教师是“八仙过海各显神通”.

一、难点突破的常规策略

1.看图识别

先让学生用“五点法”画出y=Asin（ωx+φ）的图像，比如，在同一坐标系下画出）的图像；然后观察某些特殊点的变换情况，例如，图像由y=sin2x变换到）时，原点发生了怎样的改变，平移了多少个单位；之后再组织学生多画几个特殊函数的图像，最后总结出图像变换的规律.

除此之外，还可以借助几何画板等软件，模拟演示函数y=Asin（ωx+φ）中各参数A、ω、φ对图像的影响，从中得出结论：参数A决定图像的最高点与最低点，参数ω决定函数的周期，参数φ决定函数左右平移的单位.通过不断的演示，最后得出在ω、φ的共同作用下，函数图像到底会发生哪些变化，并提炼出图像变换的规律.

借助图像提炼规律的优点是直观形象，思维门槛比较低，学生容易记忆变换的规律.但缺点也是显而易见的，那就是思维的严密性欠缺，通过几个特殊的函数与特殊的点，能否保证所得到的结论一定正确？教学实践证明，用这种方法得到的结论虽然容易记忆，但也容易遗忘和混淆.由此可见，图像的变换规律学生其实并没有真正理解与掌握.

2.解析突破

为了保证推理的严密性，很多老师又想办法从函数解析式入手，通过代数变换研究图像变换.比如，设点P（x，y）是函数y=sinx的图像上任意一点，将点P（x，y）沿x轴向左平移个单位，得到点因为点P满

1足函数所以点P在函数1的图像上；同理，反之也成立.所以函数）的图像是由函数y=sinx的图像向左平移个单位得到的.令（fx）=于是就得到结论：（fx）→函数图像向左平移个单位.之后再通过具体的函数例子作进一步验证，最终得到函数图像平移的一般结论：（fx）→（fx+φ），若φ＞0，则函数图像向左平移φ个单位；若φ＜0，则函数图像向右平移|φ|个单位.同理，也可以得到函数图像其他变换的一般化结论，于是，对于复杂的y=Asin（ωx+）图像变换，只需要分析它的解析式就能准确找到变换规律.

毋庸置疑，从解析式入手分析函数图像的变换规律，有助于学生透过表象发现函数图像变换的本质，并且可以把变换规则轻易地推广到其他类型的函数.但这种方法的弊端也是显而易见的，那就是过于抽象，若学生的思维层次没有达到一定的高度是很难理解与掌握的.

二、路在何方？

如果把上述两种教学策略有机地融合在一起，就能够兼顾图像的直观性与解析式的严密性，从而使学生获得一个比较完整的认知.但数形的完美结合离不开媒介的辅助，那么这两种教学策略的媒介是什么？

我们知道三角函数是刻画现实世界中周期运动的重要模型，尤其是匀速圆周运动，因此三角函数又称为“圆函数”.从任意角、任意角三角函数、同角三角函数关系、诱导公式，再到三角函数图像，单位圆模型都贯穿其中，无不体现“圆函数”特征.因此，单位圆模型才是三角函数的核心，也是联系数与形的纽带.于是突破本节课的难点的关键是构造函数y=Asin（ωx+φ）的现实模型，这样不仅可以让学生理解图像变换的本质，而且可以揭示各个参数的现实意义.

三、基于单位圆模型的教学尝试

1.数学模型搭台

先复习回顾定义阐述三角函数是刻画周期现象的重要数学模型，然后展示现实生活中匀速圆周运动的摩天轮画面.

问题1：如图1，设摩天轮的中心与地面距离为h0，其半径为1，摩天轮按逆时针做匀速转动，角速度为1rad/min（每分钟转动1弧度）.

假如有乘客在摩天轮上的P点处，若P点从图1中的P0点处开始计算时间，则能否计算出在确定时间tmin时，乘客的高度h？

解析：容易得到乘客的高度h=sint

问题2：假如乘客在摩天轮上的P点处，若P点从图2中的P1点处开始计算时间，则能否计算出在确定时间tmin时，乘客的高度h？

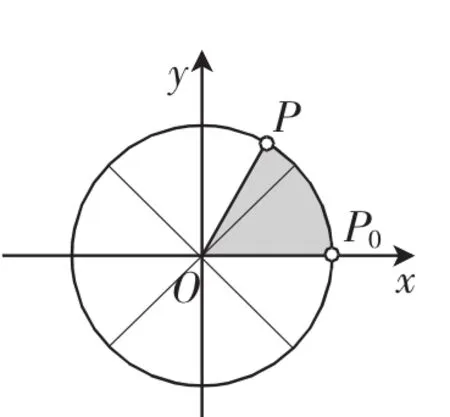
图1

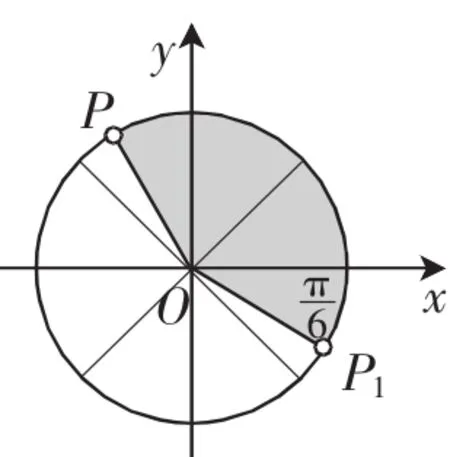
图2

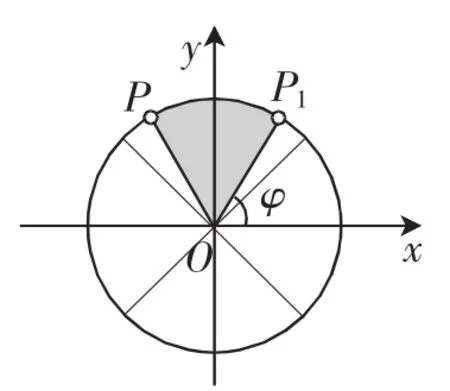
图3

问题3：假如摩天轮的半径为A，摩天轮按逆时针做匀速转动的角速度为ωrad/mim，若从图3中的P1点处开始计算时间，请问：在确定时间tmin时，乘客的高度h？

解析：此时乘客的高度为h=Asin（ωt+φ）.

意图：引导学生进行简单的数学建模，让学生感受函数y=Asin（ωx+φ）是刻画自然界周期现象的重要数学模型，具有丰富的自然背景.借助实际意义来加强理解函数y=Asin（ωx+φ）的图像性质是自然的、清楚的、明白的.

2.数形和谐共奏

如图4，从图像的视角可以得到：

从解析式的视角可以得到：

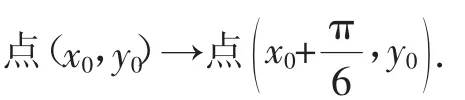
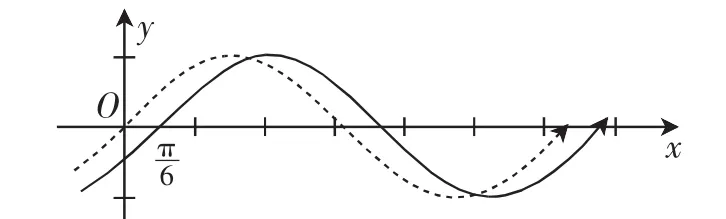
意图：通过画图，从数和形两个视角感受图像变换的情况，初步体会图像变换的规则.

问题5：对于上述图像变换，能否从圆周运动（摩天轮）的角度给出一个合理的解释？

假设两个质点A、B，它们都在半径为1的圆上、以1rad/min的角速度做匀速圆周运动.因为它们的起点相差rad，角速度均为1rad/min，所以两个质点相继经过圆上同一位置的时间差是定值为min，即从P开始运1动的B点比从P0开始运动的A点达到同一位置时相对晚了min（同一周期内）；相应地，函数y=sinx图像上的点A与函数图像上的点B高度（纵坐标）相同时（同一周期内），因为B比A晚了所以B点的横坐标要比A点的横坐标大，又因为点A是任意的，所以函数的图像可以看成是将函数y=sinx的图像向右平移个单位而得到的.

问题6：函数y=sinx与y=sin（x+φ）的图像有怎样的关系？用摩天轮模型进行解释.

意图：借助函数模型，联系生活实际，理解图像变换的现实意义，从而加深对图像变换本质的进一步理解.同时，让学生掌握先从熟悉的、特殊的问题入手，再类比研究相对陌生的、一般化的问题，最后总结出研究问题的一般方法.

本节内容具有较高的育人价值，对于学生“四基”、“四能”的培养有重要作用，同时是发展学生数学素养的重要载体.在本节课中，首先通过创设真实的生活情境，引导学生用数学的眼光观察世界，抽象出数学问题；然后，让学生在情境中经历建立模型、分析模型的过程，发展学生数学建模的核心素养；最后，在归纳和验证图像变换规则的过程中，以现实意义为媒介架起数与形之间的桥梁，实现了直观想象素养与逻辑推理素养的有效提升.F