大道至简
——从浙江省新高考两道考题说起
☉浙江省杭州高级中学钱江校区 俞 昕
浙江省新高考已经顺利实施了两年,细细品味这两年的数学卷,我们可以从中得到很多启示.两卷中“立体几何小题”具有共同之处.
2017年第9题:如图1,已知正四面体D-ABC(所有棱长均相等的三棱锥),P,Q,R分别为AB,BC,CA上的点,AP=PB=2,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α,β,γ,则( ).
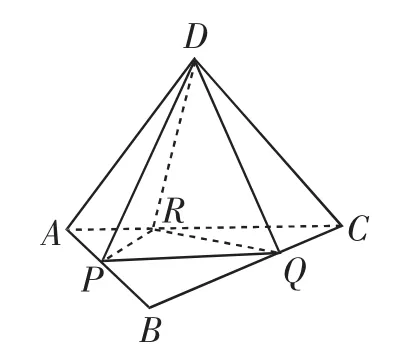
图1
A.γ<α<β B.α<γ<β C.α<β<γ D.β<γ<α
异曲同工的是2018年第8题:已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的为θ2,二面角S-AB-C的平面角为θ3,则( ).

无独有偶,笔者所在的高三备课组在二轮复习中通过集体备课开设了一节“立体几何中角的大小比较”的研讨课,下面把这节课与大家作简要分享,并进行深入的分析与反思.
一、选题缘由
高中立体几何分为传统逻辑推理法和空间向量坐标法,目前浙江卷解答题中的立体几何问题一般都可以运用这两种方法来解决.在这两种方法都可以选择的前提下,根据笔者的教学经验,大部分学生都会选择空间向量坐标法,这在一定程度上削弱了学生的逻辑推理能力.因此在教学中我们应该注重培养学生逻辑推理的核心素养,高考的指挥棒也有意识地在往逻辑推理方向倾斜,而这恰好体现在立体几何小题中,2017年第9题就是一个很好的范例.由此,笔者所在的高三备课组在二轮专题复习中开设“立体几何中角的大小比较”研讨课,强化学生运用空间角的概念对三种空间角进行定性分析,熟悉常规的空间几何模型.
二、课例简介
1.能力测评
测评1:如图2所示,已知正四面体P-ABC,E是PA的中点,F是BC上靠近点B的三等分点,设EF与PA、PB、PC所成角分别为α,β,γ,则( ).
A.β>γ>α B.γ>β>α C.α>β>γ D.α>γ>β
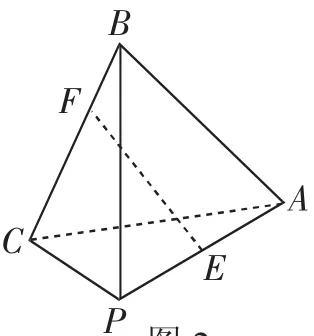
图2
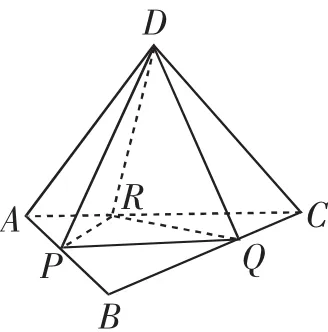
图3
测评2:(2017年第9题)如图3所示,已知正四面体DABC,P、Q、R分别为AB、BC、CA上的点,AP=PB,分别记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α,β,γ,则( ).
A.γ<α<β B.α<γ<β C.α<β<γ D.β<γ<α
设计意图:测评1仅涉及异面直线所成角(简称线线角),通过平移将空间角转化为平面角,在三个三角形中通过简单估算便可以得到大小关系,答案为D.测评2就是2017年浙江卷第9题,此题仅涉及二面角(简称面面角),利用三垂线法作出二面角的平面角,然后在三个直角三角形内通过简单计算便可得到答案B,底面正三角形如果作图精确的话,不算也能快速得到答案.可以发现2017年第9题是一个基本概念题,要求理解二面角的概念,同时考查直观想象与运算等相关素养.此题解法虽多,但转化为判断△ABC的中心到△PQR各边的距离大小,然后通过画图观察较为快捷.通过两个测评让学生回顾空间角的概念,体会传统作角的根本就是将空间角转化为平面角.
2.基于测评的提升
提升1:如图4所示,已知三棱锥D-ABC,记二面角C-AB-D的平面角为θ,直线DA与平面ABC所成角为θ1,直线DA与BC所成角为θ2,则( ).
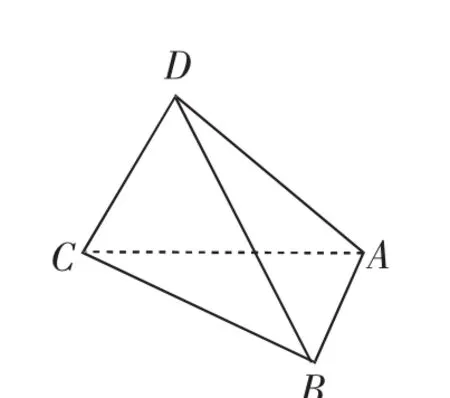
图4
A.θ≥θ1B.θ≤θ1C.θ≥θ2D.θ≤θ2
提升2:如图5所示,已知正方体ABCD-A1B1C1D1的边长为1,点E、O分别在线段BD和BD上11BO,动点F在线段AA上,且满足AF=λAA11别记二面角F-OB1-E,F-OE-B1,F-EB1-O的平面角为α,β,γ,则( ).

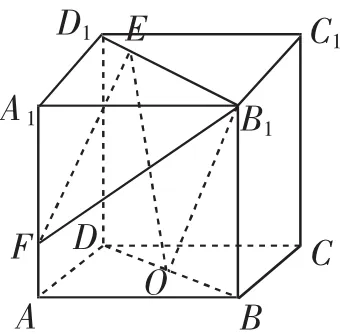
图5
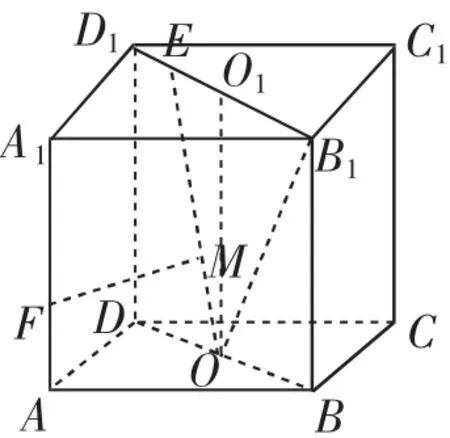
图6
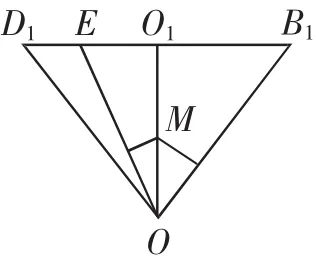
图7
设计意图:提升1其实就是构造“鳖臑”(三节棍型三棱锥),“鳖臑”是一个经典立体几何图形,它的四个面都是直角三角形,而此题中所涉及的线线角、线面角和面面角均蕴含在这些直角三角形中,答案是A.如图6,取B1D1的中点O1,M为F在平面OB1E内的射影,然后将三个二面角的平面角均转化为图7所示的平面图形中,进而比较线段长度即可.答案是D.让学生深入了解空间角的本质,掌握把空间问题转化为平面问题来解决的重要思想方法,同时又熟悉“鳖臑”这类经典立体几何图形,因为很多立体几何问题都可以在“鳖臑”中得到解决.
3.目标检测
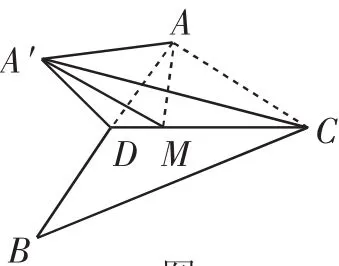
图8
目标检测1:如图8所示,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A′CD,所成二面角A′-CD-B的平面角为α,则( ).
A.∠A′DB≤α B.∠A′DB≥α
C.∠A′CB≤α D.∠A′CB≥α
目标检测2:如图9所示,已知等腰△ABC的底边BC上一点P满足CP≤CB,将△CAP沿AP翻折至△C′AP,使二面角C′-AP-B为,记直线C′A,C′B,C′P与平面ABP所成角分别为α,β,γ,则( ).

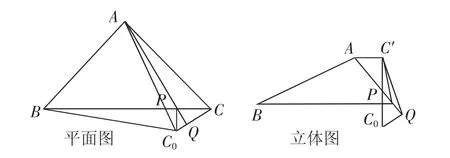
图9
设计意图:目标检测1和2是动态立体几何问题中典型的翻折问题,空间向量法在解决这样的问题时就显得使不上力了,因此充分体现了传统立体几何作角的重要性.目标检测1中只需作AM⊥CD,翻折以后垂直关系没有变,即A′M⊥CD,所以∠AMA′就是二面角A′-CD-B的平面角α的补角,于是在△AMA′和△ADA′中比较∠AMA′和∠ADA′的大小,进而得到答案B.目标检测2的关键仍然是二面角的平面角的作法,难点是确定点C′在平面ABP内的射影C0的具体位置在哪里.在图8平面图中过点C作CQ⊥AP并延长,翻折后形成了平面ABP的一个垂面,则点C′在平面ABP内的射影C0便落在垂面内,如图9立体图所示C′C0⊥平面ABP,于是要比较α,β,γ的大小,即比较图9平面图中线段C0A,C0B,C0P的大小,答案为C.通过分析,我们发现这两个动态翻折问题的本质仍然是将空间问题平面化,最后落实到比较线段长度的大小问题上.
三、回首考题
让我们回首2018年浙江省新高考卷中的立体几何小题,其同样蕴含着类似的思想:立体几何问题尽量转化为平面几何问题来处理,通过平面化将角的大小的比较问题转化为三角形内线段长度的比较问题.
2018年第8题:已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则( ).

不难发现,此题考查基础概念,对三种空间角进行定性的分析,利用常规模型.如图10所示的“鳖臑”中的结论:线线角θ1≥线面角θ2,如图11所示的“鳖臑”中的结论:面面角θ3≥线面角θ2,可得题中有:面面角θ3≥线面角θ2≤线线角θ1,再由图12知=cosθ3,过点O作AB的平行线MN交直线EF于点G,即得线线角θ1≥面面角θ3.若考生基础扎实,则无需计算,通过观察即可得到.如图13的坐标化处理,就感觉小题大做了.
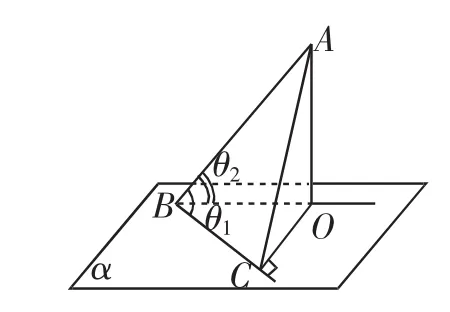
图10
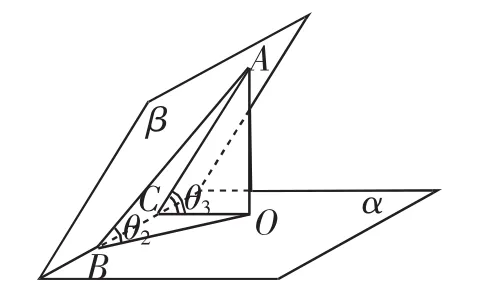
图11
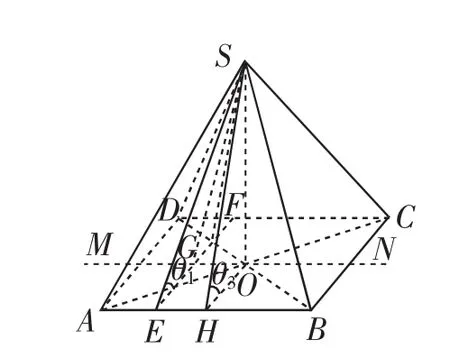
图12
通过以上的课例和两年浙江省高考立体几何小题可以发现,即使是较复杂的问题也能转化为最本质的问题,用一个词形容就是“大道至简”.大道至简的意思是指大道理(基本原理、方法和规律)是极其简单的,简单到一两句话就能说明白,所谓“真传一句话,假传万卷书”.真正的智慧就是洞察事物的本质和相互之间的关系,本质的东西看起来都很简单,但本质的来源却是错综复杂的.所以我们教学生学习数学,就是要教会学生运用最本质的东西来解决复杂的问题.做到大道至简,数学的学习就不再枯燥乏味、苦涩艰难,它将变成一种富含乐趣的探索过程.

