着眼于矛盾落实设问教学的实践与反思

☉江苏省海门中学 杨智慧

教师在授课中往往会着眼于矛盾的激发并借此来引导学生在思考与讨论中进行自主探索，因此，怎样站在矛盾的焦点上引导学生探索成为了广大教师共同关注的问题.笔者参加青年教师基本功比赛之后获得了一定的感悟和思考，借助教学的某些实践性片段与同仁们作一定的交流.

一、课堂教学片段

问题情境：取一张长方形16K白纸并在距底边一定距离处取一点F，现将白纸进行折叠并使每次折叠时的底边都能经过点F，折叠20至30次后形成一系列折痕，如图1所示，观察折痕所围轮廓，用光滑的曲线将其连起并使其与折痕均相切，形成的曲线是怎样的呢？

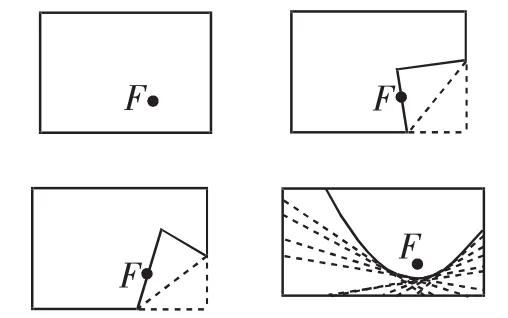
图1

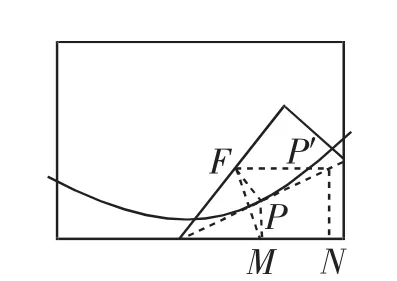
图2

追问：对折痕所围轮廓为抛物线，可以如何进行说明？

生1：底边与点F能确定一条抛物线这是比较清晰的，因此可将其设为C，如图2.在直线底边上作点F关于折痕的对称点M，并过点M作MP与底边垂直，与折痕相交于点P，可知PF=PM，即点P到定底边的距离等于点P到定点F的距离，因此，点P在抛物线C上.另外，取折痕上异于P的一点P′，过P′作NP′与底边垂直，可知FP′≠P′N，因此点P′不在抛物线C上，这就意味着折痕跟抛物线之间只存在一个交点，由此可知折痕为抛物线的一条切线.也就是说，折纸后所得的若干条切线将该抛物线包围了起来.

问题1：大家在生活和数学学习中可曾关注到一些抛物线呢？

生2：喷泉.

生3：铅球被扔出去后的轨迹.

生4：投三分球.

生5：二次函数的图像.

……

师：生活中时时处处都有抛物线的痕迹，由此可见抛物线在我们生活中的重要性，不仅如此，抛物线在科学技术等范围的应用也很广泛，那么大家知道什么叫抛物线吗？请大家回忆：平面上不在直线l上的定点F到定直线l距离相等的点的轨迹即为抛物线.点F和直线l则被分别称作该抛物线的焦点与准线，通常用字母p来表示焦点F到准线l的距离，称作抛物线的焦参数.

（运用几何画板进行抛物线形成的演示）

追问：大家认为哪个点在抛物线的所有点中是较为特殊的？为什么？

设计意图：抛物线顶点建立在原点这一最佳建系方式是本节课接下来要探究的内容，此处的设计是一种铺垫.

生6：定点F到定直线垂线段的中点即为抛物线的顶点.

问题2：有同学之前提及了二次函数的图像也是抛物线，如y2相应的定点和定直线.抛物线方程和二次函数的解析式应该保持高度的一致性，从解析式求定点和定直线目前看来不可行，那是因为建立方程的过程在此时并不存在，因此，我们应对这一过程进行探索.

问题3：抛物线的方程应该怎样建立呢？

追问1：大家还记得怎样建立曲线的方程吗？

众生：①建立直角坐标系；②设曲线上动点的坐标；③看几何限制条件；④将坐标代入几何条件；⑤化简方程.就是之前归纳过的“建设限（现）代化”.

追问2：假如焦点F与准线l之间的距离为p（p＞0），坐标系应如何建立呢？

学生讨论后呈现以下建系方式，如图3：，大家能否运用定义对其进行证明呢？

师：事实上，这一问题就是寻找

分别求出以下方程：

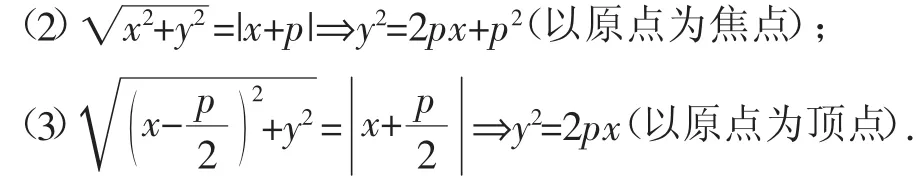
追问3：三个方程各有哪些特点？最简洁的是哪一个？

引导学生总结得出：（1）、（2） 均含有常数项，（3）最简洁.

追问4：（3）最简洁的理由何在？

学生在片刻思索之后很快将注意力放在了没有常数项上.

师：数学学科的简洁美正表现于此.

师：所以我们将y2=2px称作抛物线的标准方程，焦点到准线的距离即为p.

问题4：大家能否将椭圆、双曲线的两种形式的方程进行类比并得到其他抛物线方程呢？

学生完成表1：

表1

问题5：上述四个标准方程的共同特点是什么？怎样记忆？

学生在思考、讨论和总结后获得“一次定焦点、正负定方向”的口诀.

师：大家回头再看问题2，抛物线y=x2的焦点F、准线l分别是什么呢？

大家不约而同地感受到了初中所学的二次函数图像是不同建系下的抛物线.

课堂小结（.略）

二、教学设计的反思

1.小结

（1）引导学生在折纸活动中发现本课的研究对象并建立初步的体验与感知，折纸活动虽然在教材上也有所编排，但难度相对较大，经过改编后的折纸活动简单且易操作，笔者在通过几何画板演示动态的过程中花了较多的时间，学生在这一演示过程中的收获与课堂反馈令笔者感到欣慰，这是笔者的尝试与改编.

（2）从学生熟悉的二次函数入手说明二次函数的图像为抛物线是学生易于接受的，但证明学生不会，学生在“愤、悱”中顿时燃起兴趣的火苗，符合学生最近发展区的设计令学生对问题展开了积极的探索，学生在初中已有知识的基础上顺利构建起了新的知识体系.

（3）笔者在教学设计中比较注重学生的自主发现，将教学内容、数学思想、数学方法融合在一起，并引导学生进行探索，引导学生对研究世界的空间形式和数量关系进行深入的思考与探究，学生在领略数学刻画问题的过程中更好地感受到了数学概念及研究对象的发生、发展过程，学生在参与数学结论的发现过程与数学概念系统的创建过程中往往会获得更多的体验与感悟.

（4）笔者对于其他开口方向的抛物线的标准方程的探究设计是引导学生对椭圆、双曲线方程进行类比而获得的，学生在焦点不同、图形旋转中进行了大胆的猜测、推理与论证，这些方法上的类比很好地促进了学生能力的迁移.

（5）笔者在此课的设计中始终没有忽略“育人”的教学立足点，且在具体教学中尽量将教学提升至文化育人的高度.本课开始时设计了学生齐声朗读M·克莱因名言的环节，问题3的探究过程中引导学生对数学的简洁美进行了比较和感受，前面推导椭圆方程时引进b2=a2-c2、推导双曲线方程时引进b2=c2-a2的方法也是细微之处见精神.

2.不足

（1）提“问题”、提“好问题”是具体教学中的一项重要任务，教师可以将自己教学中想说的或者想告诉学生的都设计成问题，并令学生在问题的思考中获得答案是至关重要的.教师在学生遭遇困难时适时介入的“启”和“发”给予学生的不仅仅是茅塞顿开，更多的是思维上的拓展.笔者在处理问题的环节中投入了较多的时间，导致学生进行巩固练习的时间明显不够，在问题5上的讨论上给予学生的时间也明显不足，学生的讨论仓促而不够充分，笔者也因此过早地进行了归纳记忆与课堂小结.

（2）课堂小结也因为时间的仓促而过于简单，学生自主参与小结的过程太过简单，由此看来，有必要适当缩减之前的教学时间并为学生的小结反思预留更多的时间.

（3）课后的探究问题没有来得及布置.学生的课后思考是课堂教学的延伸，是学生对上节课所学内容的反思、体验、巩固与拓展，也是后续学习必要的铺垫，但也因为时间的不够而没有得到落实.

3.改进

教师可以运用视频展示折纸的步骤以节约时间，学生也能在直观中获得清晰的感知并顺利折出抛物线，对研究对象形成清晰感知的同时，更加容易获得成功的体验.W