新课程理念下中学数学学习过程评价的研究

☉湖南省怀化市教育局教科院 张理科

数学不仅是教学的主要学科，还是各个领域里主要的基础知识，因此对于数学学习过程的评价，一直是教育界备受关注的问题.传统模式下，我国数学教学主要是以考试的形式检测学生的数学学习情况，但这样的评价方式往往忽视了对学生学习过程的评价.随着新课程理念的不断深入，这种数学学习的评价方式已经不再适合现在学生发展的需要.［1］新课程理念下，要求中学数学教学要立足于为学生的终身学习服务，既要注重学生的学习过程评价，又要注重学生的学习结果评价，以促进学生智力和非智力方面因素的全面发展.

一、中学数学学习过程评价概述

在《普通高中数学课程标准》中明确提出：对学生数学学习过程的评价，要兼顾学生的数学学习态度、兴趣、习惯、合作状况和数学认知等的发展.中学数学学习过程评价就是有计划、有目的地对学生的数学学习态度、情感和价值观方面的学习情况进行数据收集，然后根据收集来的数据对学生的数学学习状况和自身的教学计划做出判断的过程.根据不同的评价标准，中学数学学习过程评价又可以分为不同的评价类型，其中，根据评价功能不同，可以分为诊断性评价、形成性评价和终结性评价；根据评价基准不同，可以分为相对评价、绝对评价和个体差异评价；根据评价内容不同，可以分为过程性评价和结果性评价；根据评价方法不同，又可以分为定性评价和定量评价等.［2］

二、新课程理念下中学数学学习过程评价实施策略

1.借助作业进行数学学习过程评价

作业是中学数学教学的重要组成部分，通过学生的作业完成情况，能够准确地把握学生的学习状况，也能够为学生的学习过程评价提供必要的参考依据.借助作业对学生进行数学学习过程评价主要分为以课后作业为主和以数学建模作业为主两种形式，其中课后作业主要用来评价学生对本节课知识的掌握情况，数学建模作业主要用来评价学生对本节课知识的理解和应用能力.

下面就以函数及其性质的教学为例，对以课后作业为主的评价方式进行研究.对于高一学生来说，函数并不陌生，在初中阶段就接触了函数的一些基础知识.进入高中以后，教师需要对学生函数部分知识的掌握情况有一个准确的评价，尤其是函数的定义域、值域及它们的对应关系，为此，我们可以设计以下作业来对学生进行检测评价.例：

判断下列对应关系是否是集合A到集合B的函数.

（1）A=（{x，y）|x，y∈R}，B=R，对于任意（x，y）∈A，（x，y）→x+y.

（2）A=B=N+，对于任意x∈A，x→|x-3|.

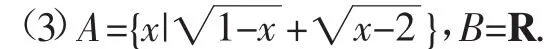
学生学完函数模型的应用以后，我们就可以通过下面的数学建模作业对学生的数学学习过程情况进行检测评价.例：

（1）电视台组织了一档抢答节目，其中有一个问题是这样设计的：小蜥蜴的体长15cm、体重15g，那么当小蜥蜴的体长为20cm时，它的体重是（ ）.（A.20g B.25g C.35g D.40g）

（2）一名乘客乘坐缆车从山上往下走，在这个过程中，他发现自己乘坐的是50号缆车，而此时离自己最近的迎面而来的依次是81号缆车、82号缆车、83号缆车，他又发现每次与对面缆车相遇的时间间隔是9s，对面缆车出现的最大数字是112.那么从与81号缆车相遇开始，50号缆车还有多久能够到站？已知索道全长1200m，那么缆车的运行速度是多少？

（3）某城市出租车收费标准如下：行程不超过4公里时，车费为10.4元，大于4公里但不超过15公里时，超出4公里的车费为1.6元每公里；行程超过15公里后，超出部分按照2.4元每公里进行计价，途中如果遇到红绿灯需要等待，按照每等5分钟收费1.6元的标准进行计算，计程器每隔半公里计价一次，例如，当行驶路程x满足12≤x≤12.5时，按照12.5公里进行计价.等候时间的计算以每2.5分钟计算一次，例如，当等候时间t满足2.5≤t≤5时，按照2.5分钟计算时间.那么如果行驶12公里，停车等候5分钟，应该付多少钱？如果行驶23.7公里，停车7分钟，应该付多少钱？如果中途没有停车等候，应付车费y就是行程x的函数f（x），求出f（x），并画出y=f（x）（0＜x＜7）的函数图像.

2.借助数学测验进行数学学习过程评价

数学测验是数学教学的重要组成部分，通过测验，教师能够及时发现教学过程中存在的问题，并及时进行改进；通过测验，学生能够检测出自身对所学的数学知识的掌握情况，下面就以函数部分的单元测试为例，借助数学测验对数学学习过程评价的实施进行说明.在学习了函数部分的相关问题之后，多数学生对函数有了大致的理解，本次测验的重点放在根据函数意义求解函数定义域和值域上面.通过题目测验，将学生的测试结果进行统计，寻找出学生集中出错的点，然后对容易出错的几个部分进行重点讲解.

3.借助学生的自我反思进行数学学习过程评价

学生的自我反思是学生对自身学习过程的主观评价，它能够体现出自身在数学学习过程中真实的情感体验.例如，很多学生会做这样的反思：“数学是我的弱科，因为找不到正确的学习方法，做题的效率较低，所以即使花费了大量的时间在数学学习上，但是成绩依然不够理想，对此我感觉非常迷茫”“我知道数学思想在数学学习过程中的重要性，但是我就是领悟不透”“数学考试的时候，书写的规范性是不是很重要”“现在的数学学习对我来说较为吃力，老师是否能够讲得慢一点，详细讲解重点部分，因为每次遇到难题就会感到无从下手”“数学学习中最大的难题就是学习的内容越来越抽象，我更加偏向于学习那些能够看得见摸得着的数学知识”.通过学生的这些自我反思，我们可以将它们分成几种情况，将不同情况的学生进行以下归类：

主动型学生：这类学生能够积极进行预习，思维较活跃，善于总结数学问题，在整个数学学习过程中会感觉到游刃有余.

按部就班型学生：这类学生按照老师的要求，会将自己学过的知识掌握得很扎实，能够就学过的知识点中的重点问题进行反思，能够在第一遍的学习中将知识点做得很详细.

中规中矩型学生：这类学生只是根据眼前的事情进行反思，不会将数学问题的深入探究列入反思计划当中，他们由于不能够及时更新知识，所以对于错题和没能领悟透彻的问题持怀疑的态度.

邋遢散漫型学生：这类学生常见于班内的后进生，他们缺乏自我监督意识，自我反思能力较差，对自己较为纵容，甚至有时候教师的劝说都不管用.

我们在数学教学过程中，可以借助学生的自我反思将他们加以分类，根据不同类型学生的实际情况，有针对性地采取措施.

三、小结

新课程理念下，要求中学数学教学要立足为学生的终身学习服务，既要注重学生的学习过程评价，又要注重学生的学习结果评价，促进学生智力和非智力方面因素的全面发展.这就要求我们在数学教学过程中，注重学生学习过程评价的多元化，能够通过不同的形式，从不同的角度对学生的数学学习进行评价.通过数学作业评价、数学测验评价和学生的自我反思评价，有效地帮助教师全面了解学生的学习状况，给学生一个客观全面的评价，从而提高学生数学学习的效率.