基于核心素养的教学设计——以“均值不等式”为例

☉江西省鄱阳县第一中学 姜 平

核心素养的课程逻辑是从“课程育人”的角度来回答“育人为本”的问题，教师更应该思考的是：学生在某节课后，到底学到了什么？除知识外，还有什么收获？本文以“均值不等式”为例谈谈基于数学核心素养的教学设计.

一、基于数学核心素养发展的教学目标

数学的课堂教学应立足于基础知识与基本技能这两方面，融入基本数学思想和基本实践活动的教学将会更好地促进学生对数学思想方法的理解、感悟、掌握和运用，只有不断积累数学活动经验，才能更好地体会数学的价值，从而提高数学学习的兴趣，增强数学学习的信心，并且这几方面密切联系、相互支撑，共同构成数学核心素养形成的基础.

“均值不等式”这节课是在学生对不等式概念与基本性质有了感性的认识之后，且能够解决简单的关于不等式性质问题的基础上，引导学生探索、发现新的问题，进一步增强数学的应用意识，以及分析问题、解决问题的能力.

二、明确基于核心素养的教材、教法分析

1.教材分析

教材（人教A版数学《必修5》）中通过对现实问题设置猜想，然后构造数学模型，从而得到不等关系；并通过引入算术平均数与几何平均数的定义，理解均值不等式的几何解释；且在此基础上进行公式的推导并学会应用.均值不等式是不等式这一章节中的核心内容，对于如何利用均值不等式求最值、值域，如何在公式推导和应用过程中渗透多种数学思想方法，这些都是学生在数学学习过程中必备的数学素养.

2.教法分析

通过对新课程标准的解读以及教材内容的解析，了解到本节课的重点是均值不等式的推导，这是形成核心素养的关键.教学中采用探究归纳、讲练结合的教学思路，体现以学生为主体，以均值不等式的形成过程为主线，放手让学生探究思索均值不等式的实质，主动发现均值不等式的应用条件及应用中常出现的错误，其中认识均值不等式成立的条件应作为本节课的难点.

3.教学流程图

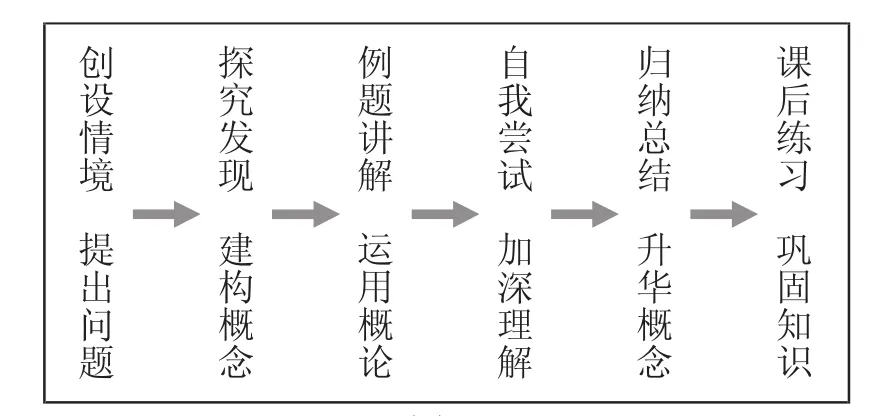
图1

三、创设情境，设置实际问题，提出问题

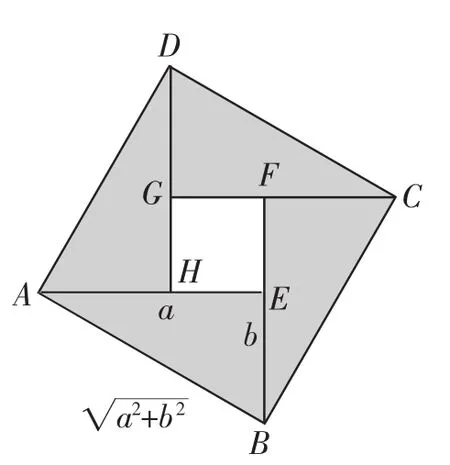
图2

1.利用赵爽弦图的模型解释a2+b2≥2ab

从古到今，中国人有很多发明创造都推动了世界的前进，在这璀璨的中华文明的浩瀚星空里，最闪亮的一颗星就是作为2002年北京国际数学家大会会徽的“赵爽弦图”.

图2所示就是在北京召开的第24届数学家大会的会标，该会标就是依据中国古代数学家赵爽的弦图而设计的，它是公元前我国数学家赵爽记录在《周髀算经》中发现和证明勾股定理的“赵爽弦图”，它比欧洲的发现早了500多年.

提出问题：在正方形ABCD中有4个全等的直角三角形，设直角三角形的两条直角边分别为a，b，那么正方形的边长为多少？这样的四个直角三角形的面积和是多少？正方形的面积为多少？结合四个直角三角形面积与正方形面积的关系能否找到一些相等或者不等的关系呢？

设计意图：教育部考试中心《关于2017年普通高考考试大纲修订内容的通知》要求“增加中华优秀传统文化的考核内容，积极培育和践行社会主义核心价值观，充分发挥高考命题的育人功能和积极导向作用.比如，在数学中增加数学文化的内容”.借助这个情景不仅引发学生强烈的民族自豪感，激发学生强烈的求知欲，并渗透爱国主义教育，同时告诉学生了解我国光辉而灿烂的数学文化史，也是提升数学核心素养很重要的途径.

探究结论：在正方形ABCD中有4个全等的直角三角形，假设直角三角形的两条直角边长分别为a，b，那么正方形的边长为这样，4个直角三角形面积之和为2ab，正方形面积为a2+b2，由于4个直角三角形面积之和小于正方形面积，于是我们就得到了一个表达式a2+b2＞2ab，当直角三角形变为等腰直角三角形，即a=b时，小正方形EFGH缩为一个点，这时有a2+b2=2ab.

得出结论：如果a，b∈R，那么a2+b2≥2ab（当且仅当a=b时取“=”），具有这种形式的式子就是我们今天要讨论的均值不等式.

教学反思：数学思维是促进数学知识和思想方法以及情感态度等数学素养的必要条件.本节课的教学过程，教师通过这一实际数学模型对数学思维价值进行挖掘，设计出有利于这些思维价值放大的探究活动，并通过学生的活动，将这种“思维形式”内化为自己的“思维习惯”.教师要善于设计数学问题作为活动进行的杠杆，把学生的思维调动起来，从而达到通过启发诱导、探究深入教会学生思考的目的.

四、设计教学活动，拓展公式内容，增强学生的逻辑推理能力

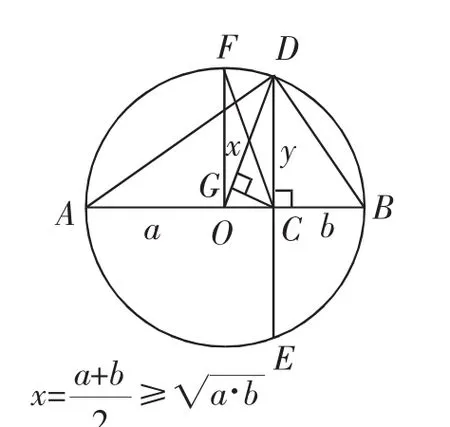
图3

数学教学就是学生在各种数学活动中生成、拓展、提升与交流经验的过程，同时是他们获得数学基础知识、基本技能与基本思想的过程.教师通过教学活动给学生创造直观思维的机会，通过层层的问题设置给予学生“悟”的时间和空间.

教学活动设计：如图3，AB是圆O的直径，点C为AB上一动点，CD垂直AB交圆O于D，E两点，连接AD，BD，OD，点F为圆O上的点，且OF⊥AB，连接CF，过C作CG⊥OD，交OD于点G.设AC=a，BC=b.不妨设a＞b.

圆中有四条线段的长度分别等于不等式中的四个数，你能看出这四个数分别对应于哪条线段吗？

设计意图：这个图形是我们非常熟悉的一个重要图形，由于半弦长不大于半径，故得到不等式继而得到其他不等式（a＞0，b＞0，当且仅当a=b时取等号），同时，对于上述不等式，当且仅当a=b时半径等于半弦，等号成立.本节课利用这个圆中的线段模型，使学生从均值不等式的几何解释中体会到了证明均值不等式的常用方法，也体会到了不等式成立的相关条件，使学生具备进一步应用均值不等式解题的基础.F