挖掘题目内涵 提高复习效率
☉江苏省苏州市吴中区木渎金山高级中学 姜 慧
“教师讲的多、学生听的多”,在高中数学课堂教学中已经成为一种极为普遍的现象,因此形成了“教师展示多、学生看的多”的局面,在普遍的教师自问自答的模式下很多学生养成了随声附和的习惯,因为教师的直接给出导致学生在教学重、难点的把握上也变得似懂非懂,学生看上去听懂了,但自主练习时往往很少能正确解题,因此“教师教得苦、学生学得苦”的局面的形成也就不足为怪了.
怎样令数学课堂成为教师与学生都能开怀的乐园一直是笔者的追求,本文结合一道习题教学来浅谈笔者在解题教学中的一点思路.
这是在高三一轮复习中遇到的一个题目,笔者在实际教学中首先将题目进行了展示.
题目 设集合A={x|x2+2x-3>0},集合B={x|x2-2ax-1≤0,a>0}.若A∩B中恰有一个整数,则实数a的取值范围为______.
笔者给予了学生充分的思考时间并进行了巡视,发现很多学生在思考与探索中得到了以下解题过程:
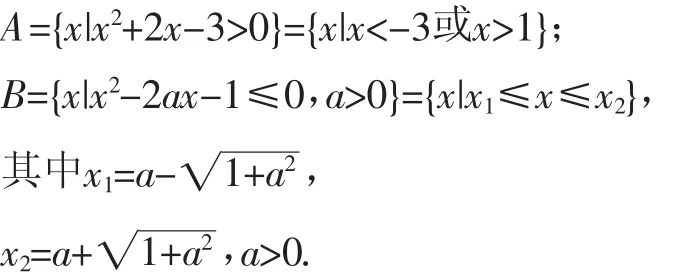
但学生对后续解题应如何进行不知所措,笔者对这一情况进行了及时的通报并启发学生对后续解题进行思考与探索.
生1:题目要求的是a的取值范围,这必然要根据“A∩B中恰有一个整数”这一条件来进行分析,因此应首先求出A∩B,但A∩B并不易求得,因为B中含有字母,因此可以考虑分类讨论.
师:求A∩B的关键在什么地方?
师:你会比较其中关系吗?
师:其他同学可否帮忙来判断这两者之间的大小关系呢?
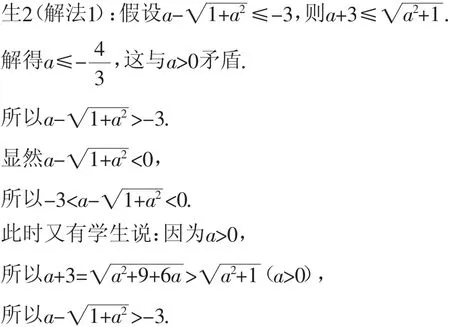
师:太棒了,如此我们就能得出(如图1).根据条件“A∩B中恰有一个整数”可知该整数必然为2,所以解得
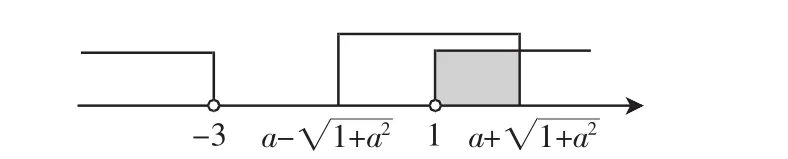
图1
此时有学生跃跃欲试且表现出十足的把握.
师:说说看.
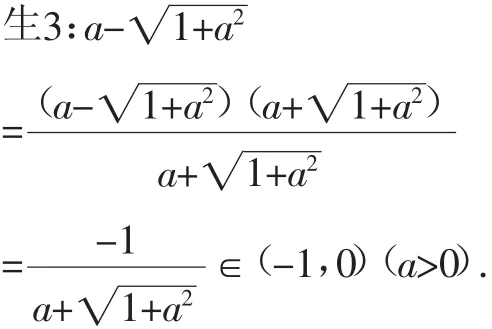
师:太棒了,真没想到你居然能够想到用分子有理化这一思路!
其他学生的情绪与斗志因为生3受到表扬而受到了鼓舞,又有学生发言了.
生4(解法2):我的解法不一样,我没有对B中的不等式进行求解.
师:这个方法可行吗?你说说看!
生4:令f(x)=x2-2ax-1(a>0).设其两个零点分别为x1和x2,且x1<0<x2(x1x2=-1<0).
由A={x|x<-3或x>1},若A∩B中恰有一个整数,则该整数只能是-4或2.

(1)如果该整数是-4,这与a>0矛盾,因此该整数不可能是-4.(2)如果该整数是2,

根据(1)、(2)可知,该整数只能是2.

师:很好!不对B中的不等式求解居然也能求得实数a的取值范围,这是不是有点令人出乎意料啊?实际上,这一解法是对零点存在性定理的运用,对于大多数同学的思维来说,这是一个全新的视角,那么大家对以上两种解法有何感想?大家觉得这两种方法有何优劣呢?
学生的议论声顿时从教室的各个角落传来.此时,被大家称为“数学王子”的学生站了起来,这是一个经常能够表达独特思想的优秀生.
生5:我是这么想的,假如将题目中的“A∩B中恰有一个整数”这一条件改成“A∩B中恰有两个整数”的话,运用解法2来求解实数a的取值范围可能会复杂得多,应该要用到分类讨论.此时若运用解法1来求a的取值范围,应该会比较好,只要解不等式即可.同理,条件中整数的个数可以扩展为三个、四个…
师:这就是变式和拓展了,非常好,学习数学如果能够展现出这些变式与拓展的思维就会觉得数学有意思了.
(此时,数学课代表将手举了起来)
生6(解法3):解法2应该是可以简化的.在之前的解法中已经对该整数进行了分析,只能是-4或2.
(1)假如该整数是-4,那么令(fx)=x2-2ax-1(a>0).
因为(fx)=x2-2ax-1(a>0)的对称轴为x=a>0且左零点x1应满足:x1∈(-5,-4],所以右零点应满足:x2>4.
这样的话,A∩B中就不仅仅只包含一个整数了,至少包含2、3、4这3个整数.
因此,这种情况是不成立的.
(2)假如该整数是2,那么由于x1x2=-1<0,因此必有正根x2落在[2,3)内,

根据(1)、(2)可知,该整数只能是2.

教师在实际教学中应对习题、例题多加研究,挖掘一些内涵丰富但求解过程不太复杂的题目,引导学生在这些题目的思考、挖掘与探索中进行全方位的研究,使学生能够在一道题的思考与解决中获得完整的知识体系的建构,美国著名数学教育家波利亚也曾在这方面提出过相同的观点.当然,要令学生在解题中有所收获,教师应首先对试题、习题、例题进行深入的研究,然后在课堂教学中对学生进行充分的激励和引导,使学生真正成为数学学习的主人并发表不同的见解,使学生的思维之火熊熊燃起,从而与教师共同构筑快乐的数学学习乐园.F

