圆锥曲线中直线过定点问题探析

☉甘肃省兰州市第十中学 温庆峰

“定点”问题是圆锥曲线常考题型，注重知识的综合，更注重数学思想方法的应用，难度较大.纵观近几年高考，圆锥曲线中直线过定点问题频频出现，下面类比探析其相似性.

命题1：已知抛物线C：y2=2px（p＞0），过定点（t，0）（t＞0）且不垂直于x轴的直线l与抛物线C交于M，N两点，则在x轴上存在点P（-t，0），使得∠OPM=∠OPN.

例1（2018年全国新课标卷Ⅰ文）设抛物线C：y2=2x，点A（2，0），B（-2，0），过点A的直线l与C交于M，N两点.

（1）当l与x轴垂直时，求直线BM的方程；

（2）证明：∠ABM=∠ABN.

解析：（1）当l与x轴垂直时，l的方程为x=2，代入y2=2x，得M（2，-2），N（2，2），或M（2，2），N（2，-2），所以BM的方程为2y+x+2=0，或2y-x-2=0.

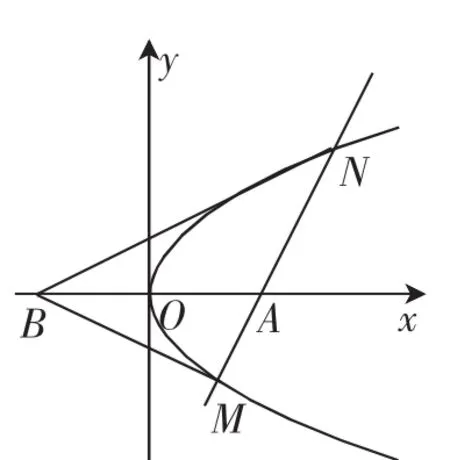
图1

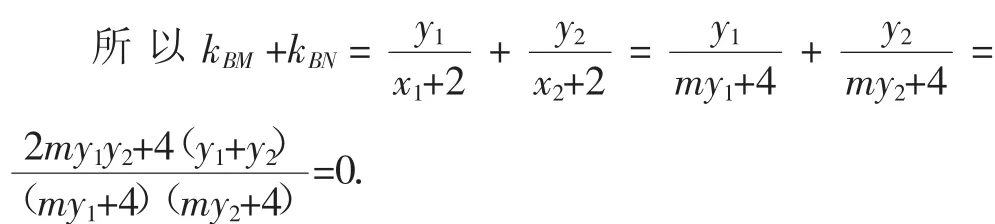
所以kBM=-kBN，所以∠ABM=∠ABN.

拓展：已知抛物线C：y2=2px（p＞0），过定点（t，0）（t＜0）且不垂直于x轴的直线l与抛物线C交于M，N两点，则在x轴上存在点P（-t，0），使得∠OPM+∠OPN=180°.

命题2：已知抛物线C：y2=2px（p＞0），点P（-t，0）（t＞0），设不垂直于x轴的直线l与抛物线C交于M，N两点，若∠OPM=∠OPN，则直线l过定点（t，0）.

所以kt+b=0，故直线l的方程为y=k（x-t），即直线l过定点（t，0）.

（1）当l与x轴垂直时，求直线AM的方程；

（2）设O为坐标原点，证明：∠OMA=∠OMB.

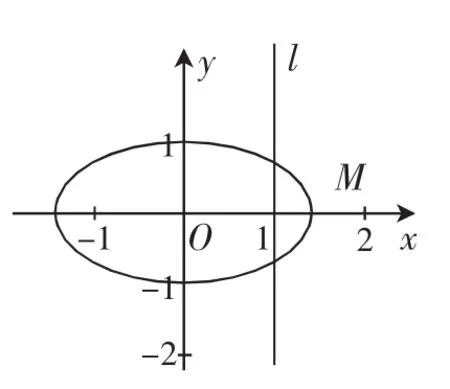
图2

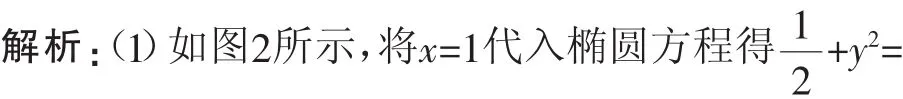
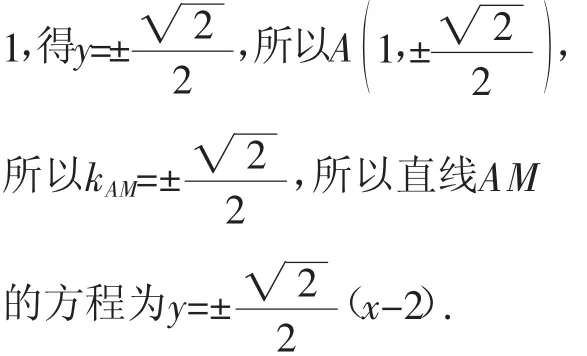
（2）当l的斜率不存在时，由（1）可知，结论成立；当l的斜率存在时，设其方程为y=消去y得（2k2+1）x2-4k2x+2k2-2=0，所以x1+x2=，x1x2=

（1）求椭圆C的方程；

（2）已知A，B为椭圆长轴的两个端点，作不平行于坐标轴且不经过右焦点F的直线PQ，与椭圆交于P，Q两点，若满足∠AFP=∠BFQ，求证：直线PQ恒过一定点.

解析：（1）依题意知l：y=x-c. ①

所以kt+m=0，故直线l的方程为y=k（x-t），即直线l过定点（t，0）.W