基于教材提升学生数学素养的变式教学*

☉甘肃省渭源县第一中学 何伟军

教材中的许多例题都有着丰富的内涵，都是经过教材编写专家精心挑选的，因此绝大多数教材例题、练习题、习题和复习参考题（简称教材“四题”）都具有可变性和可研究性，为此我们开展对教材“四题”的变式研究，进一步夯实学习以及未来发展所必需的“数学基础知识、基本技能、基本思想、基本活动经验”（简称“四基”）.基于教材，创设合理的教学情境；基于“最近发展区”，拓展学生的认知，在落实“情境与问题、知识与技能、思维与表达、交流与反思”的过程中助推学生数学核心素养的培养.

源题（人教A版必修2第127页）如图1，已知直线l：3x+y-6=0和圆心为C的圆x2+y2-2y-4=0，判断直线l与圆C的位置关系；如果相交，求出它们交点的坐标.

（解答详见课本第127页内容，此处略）

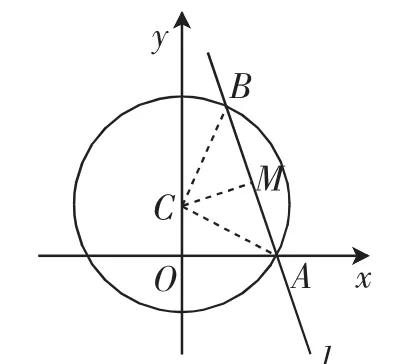
图1

一、条件不变，改变设问方式

通过改变设问方式，实现变式，以检测学生对所学知识的掌握程度，帮助学生获得必要的“四基”，从而促进学生的学习.

变式1：求直线l：3x+y-6=0被圆C：x2+y2-2y-4=0截得的弦长.

路径1：由例题易求得直线l与圆的两个交点坐标分别是A（2，0），B（1，3），再利用两点之间的距离公式得

评注：这种基于学生“最近发展区”的解法信手拈来，思路自然流畅，学生易懂，属于典型的通性通法.

路径2：采用“设而不求”的方式.将直线方程代入圆C的方程中得x2-3x+2=0，设两交点分别为A（x1，y1），B（x2，y2），则由根与系数的关系得x1+x2=3，x1x2=2.

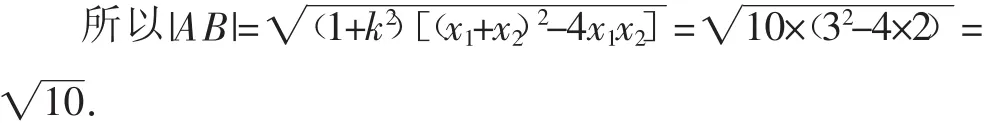
评注：“设而不求”是研究直线与圆锥曲线位置关系时常用的技巧，我们无需具体求出直线l与圆的两个交点，只需应用弦长公式、凑配整体代入即可求解.

评注：利用圆半径、弦心距、弦长之半构成直角三角形求解，这也是解决有关直线与圆问题的通法.

变式2：设直线l：3x+y-6=0和圆C：x2+y2-2y-4=0相交于A，B两点，求弦AB的垂直平分线的方程.

解析：将圆C的方程化为x2+（y-1）2=5，圆心为C（0，1），直线l：3x+y-6=0的斜率k=-3，所以弦AB的垂直平分线的斜率为，所以弦AB的垂直平分线的方程为y-1=（x-0），即x-3y+3=0.

评注：根据弦AB的垂直平分线经过圆心，用直线的点斜式方程容易求解.

二、引进参数，增设分类讨论

引进参数，适度增加试题的思维量、运算量，问题设置要承上启下，注重基础，要具有一定的探究性.

变式3：已知直线l：y=kx+6与圆C：x2+（y-1）2=5.当k为何值时，直线l与圆C相交、相切、相离？

因为Δ=（10k）2-80（1+k2）=20k2-80，所以：

（1）当Δ＞0，即k＜-2或k＞2时，直线l与圆C相交；

（2）当Δ=0，即k=±2时，直线l与圆C相切；

（3）当Δ＜0，即-2＜k＜2时，直线l与圆C相离.

评注：利用代数法，即通过直线与圆的方程组成的方程组的解的个数来判断，归根到底是用判别式Δ进行分类讨论来作答的，在明晰问题的基础上，“数学运算”是关键，此法也适合直线与圆锥曲线位置关系的判定，故其是解决此类问题的通性通法.

评注：利用几何法，即由圆心到直线的距离d与圆的半径r的大小关系进行判断.

三、互换条件与结论，培养逆向思维

适当改变题目的条件与结论，比如可以将条件与结论互换，探究它们之间的关系，引导学生解答，能有效地提高学生的思维能力和创新能力.

变式4：已知圆C：x2+y2-2y-4=0，直线l过点M且与圆C相交于A，B两点，|AB|=，求直线l的方程.

解析：将圆C的方程化为x2+（y-1）2=5，其圆心为C（0，1），半径r=.

评注：采用待定系数法求斜率k，而圆的弦心距（圆心O到直线l的距离）是求解关于k的方程的关键.

变式5：已知圆C的圆心在y轴上，且被x轴截得的弦长为4，被直线l：3x+y-6=0截得的弦长为，求圆C的方程.

故所求圆的方程为x2+（y-1）2=5.

评注：求圆的方程的基本方法就是“选形式、定参数、列方程组”，其中运用半径、弦心距、弦长之半构成的直角三角形来列方程组是思维的核心，正确求解是落脚点.

四、引进对称，“丰富”设问

以光线反射为代表的很多实际问题，都可以转化为对称问题，教师巧妙设问，展示变式新途径，抓住对称的本质属性，从而促进学生思考.

变式6：求与圆C：x2+y2-2y-4=0关于直线l：3x+y-6=0对称的圆的方程.

解析：将圆C的方程化为x2+（y-1）2=5，圆心为C（0，1）.

所以C′（3，2）.

所以，与圆C关于直线l对称的圆的方程是（x-3）2+（y-2）2=5.

评注：根据对称的几何性质列出关于a，b的方程组是求解的中心环节.

五、引进直线系，变式更精彩

若引进直线系，运用类比、联想等思维方法，能够形成新命题，就可以帮助学生克服思维狭窄、短视性思维弊端，并帮助学生提升推陈出新的意识.

变式7：已知直线l：（m+3）x+（1-3m）y+3m-6=0，圆C：x2+（y-1）2=5，问：m为任意实数时，l与C是否相交？若相交，求出相交的弦长的最小值及此时m的值；若不一定相交，则举出一个反例.

解析：将直线l的方程整理可得（3x+y-6）+m（x-3y+3）=0.

评注：根据方程求出该直线系恒过圆内一定点，理解该定点与圆心的连线垂直于过该点的弦时，其弦长最短是关键.用数形结合思想求解更直观、更容易.

六、改装题源条件，链接高考

在习题教学中分析数学命题的条件与结论，较好地整合、处理教材习题，揭示高考母题题源，寻找命题的内在逻辑和思想方法，有助于提升学生的数学综合能力.

变式8：已知直线l：y=kx+6.（k∈R）

（1）若圆心在y轴上的圆与直线l相切于点P（2，2），求该圆的方程.

（2）若直线l关于x轴对称的直线为l′，问：直线l′与抛物线C：x2=4y是否相切？说明理由.

解析：（1）如图2，设圆心坐标为（0，b），半径为r，则所求圆C的方程为x2+（y-b）2=r2.由圆C与直线l相切于点P（2，2）知，2=2k+6⇒k=-2，即圆的切线l的方程为2x+y-6=0.

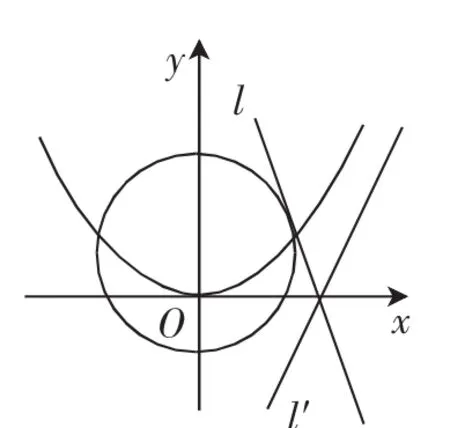
图2

（2）因为直线l的方程为y=kx+6，所以直线l′的方程为y=-kx-6.

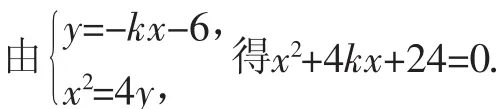
因为Δ=16k2-4×24=16k2-96，所以当k=±，即Δ=0时，直线l′与抛物线相切；当k≠±时，直线l′与抛物线不相切.

评注：本小题经过变形改造后和2011年福建省高考理科卷第17题极为相似，我们把知识的“生长点”建立在学生认知的“最近发展区”，通过学生自己的思考完成题目的解答，感悟“源于教材，高于教材”不是空穴来风，变式不是无源之水，漫无目的，在解答的过程中用基础知识做铺垫，用数学思想方法做统领，用数学语言表达问题.

七、引进极坐标与参数方程，形异质同

以基础知识为载体，把同一曲线转化为另一种等价方程，构成新情境，以检验学生对多个知识点“串联”的本领，再启发诱导学生从不同视角观察问题、分析问题和解决问题，有力地促进学生创新意识的发展.

变式10：已知曲线C的参数方程为

1（φ为参数），曲线C2的极坐标方程为3ρcosθ+ρsinθ-6=0.

（1）将曲线C1、C2的方程分别化为普通方程和直角坐标方程；

（2）问：曲线C1、C2是否相交？若相交，请求出公共弦长；若不相交，请说明理由.

解析：（1）由得x2+（y-1）2=5，所以曲，线C1的普通方程为x2+（y-1）2=5. 因为3ρcosθ+ρsinθ-6=0，令ρcosθ=x，ρsinθ=y，得3x+y-6=0，所以曲线C2的直角坐标方程为3x+y-6=0.

评注：此题只是将题源中的普通方程以参数方程或极坐标方程进行外“包装”，要求重新在新情景之中求解原问题，剥取外“包装”后发现两题形异质同.