圆锥曲线运动有心力问题的推理及动能导数法的优点分析

邵 云

（南京晓庄学院 电子工程学院，江苏 南京 211171）

在已知轨道方程的情况下，多数教科书[1-3]都是采用比耐公式来求有心力。介绍一种用质点动能Ek对矢径r求导来求有心力的方法，姑且称作动能导数法，推导出做圆锥曲线运动质点所受的平方反比引力，以及系统能量的统一表达式；与此同时，将动能导数法与比耐公式法进行了较充分的比较，发现前者的优点所在。虽然文献[4-6]已提及动能导数法，但却未继续讨论；尽管文献[7-8]明确地提出该方法并对其简便性进行了一些论证，但却未能把有心力和各种能量放在一起通盘考虑，显得研究仍不够深入。质点的角动量J→守恒是进行推理的前提，设其大小为

其中m为质点的质量，h为常量[1]。

1 从极坐标轨道方程计算质点的动能

设质点P做圆锥曲线运动如图1所示，极坐标系的极点O位于近焦点，p为半正焦弦长度，e为偏心率，则在图中的极坐标系下圆锥曲线的方程可表为

图1 质点P的圆锥曲线运动

2 将动能对矢径求导得有心力

可见，只要算得动能函数Ek（r），对其求导即得保守有心力 F（r）。

3 做圆锥曲线运动质点的动能、有心引力、势能和总能量

现将圆锥曲线方程式（2）代入动能的计算式（7）得

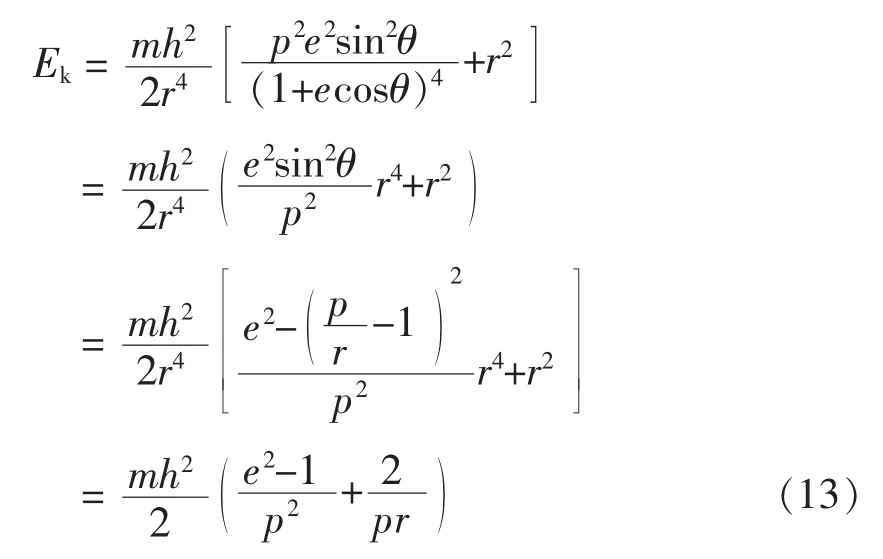
此即质点在圆锥曲线轨道上任一点的动能，它诚然是r的单值函数。将式（13）代入式（12）即得有心力：

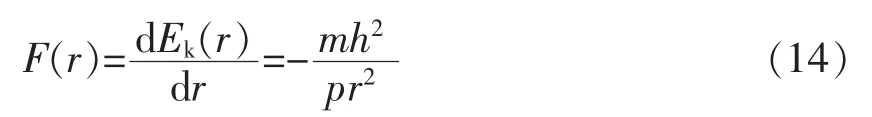
可见，圆锥曲线轨道所对应的有心力是平方反比引力（负号表示引力）。联立式（9）和式（14）得该引力所对应的势能函数为

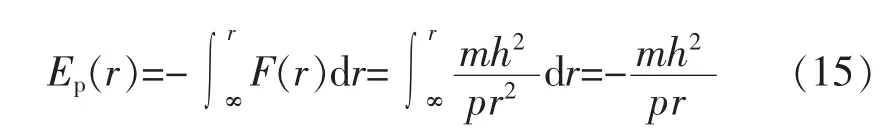
其中，已令无穷远处的势能为零，即Ep（∞）=0。再将式（13）和式（15）代入式（10）得

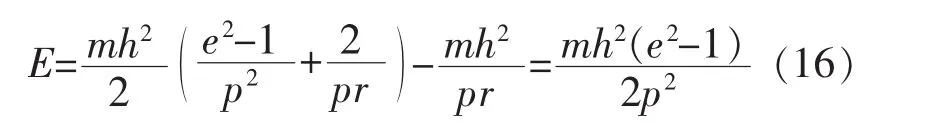
从式（14）和式（16）可见，无论有心力 F（r）还是总能量E，它们不仅依赖于轨道的形状（p和e），而且依赖于质点的质量m和角动量J（=mh）。

4 用动能导数法推导有心力问题的优点分析

在传统的教科书中，都是通过比耐公式（u=1/r）：

将式（18）代入比耐公式（17）即得有心力：

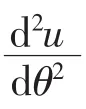
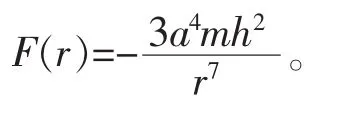
图 2 双纽线 r2=a2cos2θ（a=1）

证法一（动能导数法）：将r2=a2cos2θ两边对θ求导并整理得可见，式（46）结果与式（38）结果相同。

分别比较以上两个例题的证明过程可以发现，例1的动能导数证法显然比比耐公式证法简便，而例2的动能导数证法从实际计算量来看，也比比耐公式证法简便。文献[7]已经证明：对于很多数学上典型的轨道曲线 （注：物理上未必能实现！），应用动能导数法求其有心力似更简单。

另外，这里顺便提及一下，当已知v（r）求有心力F（r）时[9]，应用动能导数法就更直接方便了。

5 对第3节中能量结果的讨论

是一与轨道无关的内禀常量。这就表明：此时的角动量大小J=mh由半正焦弦长p来表征，而能量E的大小则由轨道参量a或a′唯一地确定。这便是平方反比引力作用下质点所做圆锥曲线轨道运动的基本特征。

6 结语

在通常的教科书中，应用比耐公式从轨道方程推导有心力问题的思路是：轨道方程→有心力→势能→总能量→动能；而本研究应用动能导数法的推理思路却是：轨道方程→动能→有心力→势能→总能量。比耐公式法的优点在于从轨道方程推导有心力的思路最直接，而动能导数法的优点不仅在于计算简便 （包括有心力的计算以及诸能量的获得），而且诸能量的含义都交待得明明白白。因此，动能导数法不失为从轨道方程推导有心力问题传统所采用的比耐公式法的有益补充。此外，根据轨道方程，将动能、有心引力、势能和总能量一系列地推导出来的研究思路，或可为相关内容的教学提供一些参考。当然，当已知有心力求轨道方程时，比耐公式是有明显优势的，这也是它被写进教科书的原因所在。