混凝土单箱双室磁浮轨道梁的日照温度场分布研究

邹 波,滕念管

(上海交通大学船舶海洋与建筑工程学院,上海 200240)

1 概述

为了适应现代磁浮交通的发展，我国正在研发适合速度600 km/h以上的高速磁浮列车以及速度为200 km/h的中速磁浮的轨道结构形式，混凝土双室箱梁具有截面刚度大、整体性好等优点，在磁浮线路中有较好的应用前景。由于磁浮列车对轨道梁的平顺度要求极高，磁浮轨道梁的变形必须严格控制，而温度作用是影响磁浮轨道梁变形的重要因素之一，具有重要的研究意义。

混凝土桥暴露在外界环境中，其温度场分布受外界环境影响很大。由自然环境引起的温度荷载主要有日照温度、骤然降温和年温变化，其中日照温度荷载和对混凝土结构作用时间短，温度分布影响大，造成的应力不均情况明显[1]。国内外很早就注意到了日照对结构温度分布及其对结构的影响，并进行了大量研究。彭友松(2007)根据太阳物理学、普通天文学及传热学的有关理论，利用ANSYS平台，编制和开发了不同类型混凝土桥结构进行日照分析的程序化模块，可以研究太阳辐射、风速、气温等对日照温度效应的影响[2]。聂玉东(2013)采用有限元程序依托嫩江大桥工程的温度场进行计算，和实测数据进行对比，验证了计算理论的正确性，同时提出了寒冷地区大跨混凝土箱梁温度梯度模式[3]。陈泗瑶(2014)分析了幸福源水库双线特大箱梁桥在日照和寒潮下的温度分布情况，拟合出了日照升温和寒潮降温下的竖向温差曲线，并基于此温差模式计算了梁截面的温度应力[4]。谢鹏等(2017)利用ANSYS分析了赤石特大桥在9月2日的温度分布情况，并与实测数据作对比，验证了有限元方法的可行性[5]。Nildem Tays等(2014)自制了1∶1箱梁试验模型，测量了某日箱梁的温度场分布情况，并研究了热传导率、热吸收率、比热容、密度、辐射系数对截面温度的影响[6]。

然而，国内外关于混凝土单室梁在日照情况下温度分布研究较多，而对单箱双室的研究较少。现行的《高速磁浮交通设计规范》[7]对磁浮轨道梁温度梯度值的选取也是以单室箱梁为基础的，对于双室箱梁的温度分布规律与单室箱梁是否具有相似性以及在进行设计时能否直接采用规范温度梯度值尚有待进一步研究。

2 太阳辐射温度场分析的基本原理

一般来说，热量传递主要分为三种方式：热传导、热对流和热辐射。热传导是由于温度梯度存在而引起内能的交换。由于桥梁的纵向长度远远大于其横向尺寸和竖向尺寸，忽略纵向温度梯度的影响，将其转化为二维传热问题[8]

(1)

式中，λ为导热系数;ρ为密度;c为比热。

热对流是指固体的表面与它周围接触的流体之间，由于温差的存在引起的热量的交换。热对流用牛顿冷却方程来描述

q=h(TS-TB)

(2)

式中，q为热流密度；h为对流换热系数；TS为固体表面温度；TB为周围流体的温度。

热辐射指物体发射电磁能，并被其他物体吸收转变为热的热量交换过程。箱梁外表面除了受太阳辐射作用，同时还与周围空气进行辐射换热和对流换热。其外部边界条件可以用下式表示[3]

(3)

式中，n为界面法向方向；ε为混凝土表面热辐射吸收系数，一般取0.5～0.7，本文取0.65；q为投射到边界面上的总的太阳辐射强度；hc为边界的对流换热系数；hr为边界的辐射换热系数；Ta为外边空气的温度。为方便计算，可将式(3)改写成第三类边界条件的形式，如下所示

(4)

式中，Tz为外边界面的综合温度，可写为Tz=εq/(hc+hr)+Ta；箱梁内部没有太阳辐射，但箱梁内表面间存在辐射换热，箱内空气与混凝土表面存在对流换热。总的换热方程为

(5)

式中，qr为各边界面的热流密度；Ta为箱内空气温度；为了方便计算，可将式(5)改写成第三类边界条件的形式，如下所示

(6)

(7)

3 日照温度场的有限元分析

3.1 计算模型

由于国内目前没有双室箱梁的高速磁浮实例，以上海某南北走向高速铁路混凝土单箱双室箱梁进行计算，截面高度为3.882 m，上顶板宽度为12.6 m，下底板宽度为6.7 m，上顶板及左中右三腹板厚度均为0.48 m，下底板厚度为0.462 m。如图1所示。

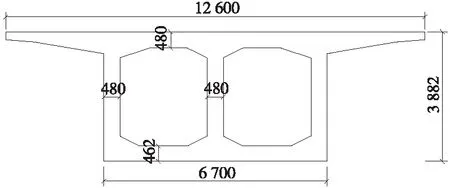
图1 单箱双室混凝土梁截面(单位：mm)

夏季白天对于南北走向箱梁来说，上下及东西表面在不同时刻受到的太阳辐射强度相差很大，基于太阳辐射和气温数据等相关资料，建立了从早上5：00到第二天04：00的箱梁日照温度场瞬态分析模型。模型采用PLANE55单元，表面用SURF153单元覆盖，全截面自由划分，网格尺寸控制为0.10 m。模型材料为C50混凝土。根据《高性能混凝土结构抗火设计原理》[9]中常用建筑材料热物理性能计算参数的规定：混凝土的质量密度ρ为2 200～2 400 kg/m3，本文取2 400 kg/m3，其导热系数λ与比热容c根据线性插值分别取为1.758 W/(m·℃)和916.7 J/(kg·℃)。网格划分后截面如图2所示。

图2 箱梁横截面网格划分示意

3.2 日气温变化

根据历年气温统计资料，上海7月份平均气温最高，由于全球气候变暖，本文基于2011～2017年7月份上海气温资料，得到上海7月份日最高气温平均值为33.78 ℃，最低气温平均值为26.89 ℃。

通常最高气温Tmax出现在下午14：00～15：00，最低气温Tmin出现在日出前。本文假设日气温出现在下午15：00，气温在一天内的变化可以表示为时间t的正弦函数形式[10]。

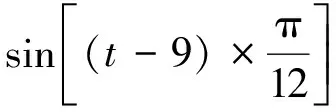
(8)

代入相应数据，可得到一天内气温随时间变化如图3所示。

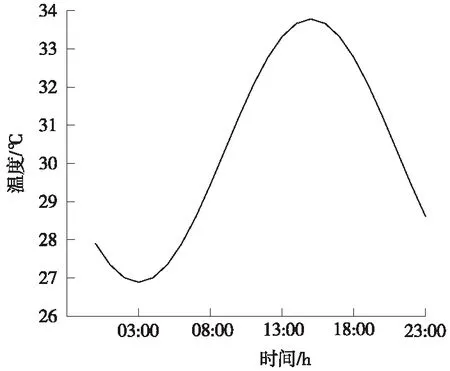
图3 气温随时间变化曲线

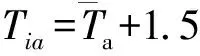
3.3 综合换热系数的计算

综合换热系数由对流换热系数和辐射换热系数之和组成，对于箱梁结构，其顶板、底板以及腹板外缘的对流换热系数分别可以表示为风速的函数[6]

顶板：hc=3.83v+4.67

底板：hc=3.83v+2.17

腹板：hc=3.83v+3.67

对于箱梁内部，其对流换热系数一般取hc=3.5 W/(m2·℃)；根据《中国建筑热环境分析专用气象数据集》[12]的相关数据，取上海夏季平均风速v=3.5 m/s，可得顶板、底板、腹板的对流换热系数分别为18.075，15.575，17.075 W/( m2·℃)

辐射换热是物体与介质之间以长波辐射的方式进行的热交换。由辐射定律可导出混凝土表面的辐射换热系数hr为空气温度Ta和混凝土表面温度T的函数，取混凝土温度比空气温度高10 ℃，hr可近似表示为[3]

hr=0.88[4.8-0.075(Ta-5)]

(9)

由于辐射换热系数随空气温度变化较小，Ta可取为日平均气温30.33 ℃，按式(9)计算得到辐射换热系数hr为5.90 W/(m2·℃)。各位置的综合换热系数如表1所示。

表1 综合换热系数 W/(m2·℃)

3.4 太阳辐射量的计算

对于在太阳照射下的混凝土箱梁，其外表面受到的总辐射由太阳直接辐射、天空的散射和地面的反射三者组成，各种辐射量可以分别根据文献[2]的方法计算得到，双室箱梁各个表面不同时刻的太阳辐射总量计算结果如表2所示。

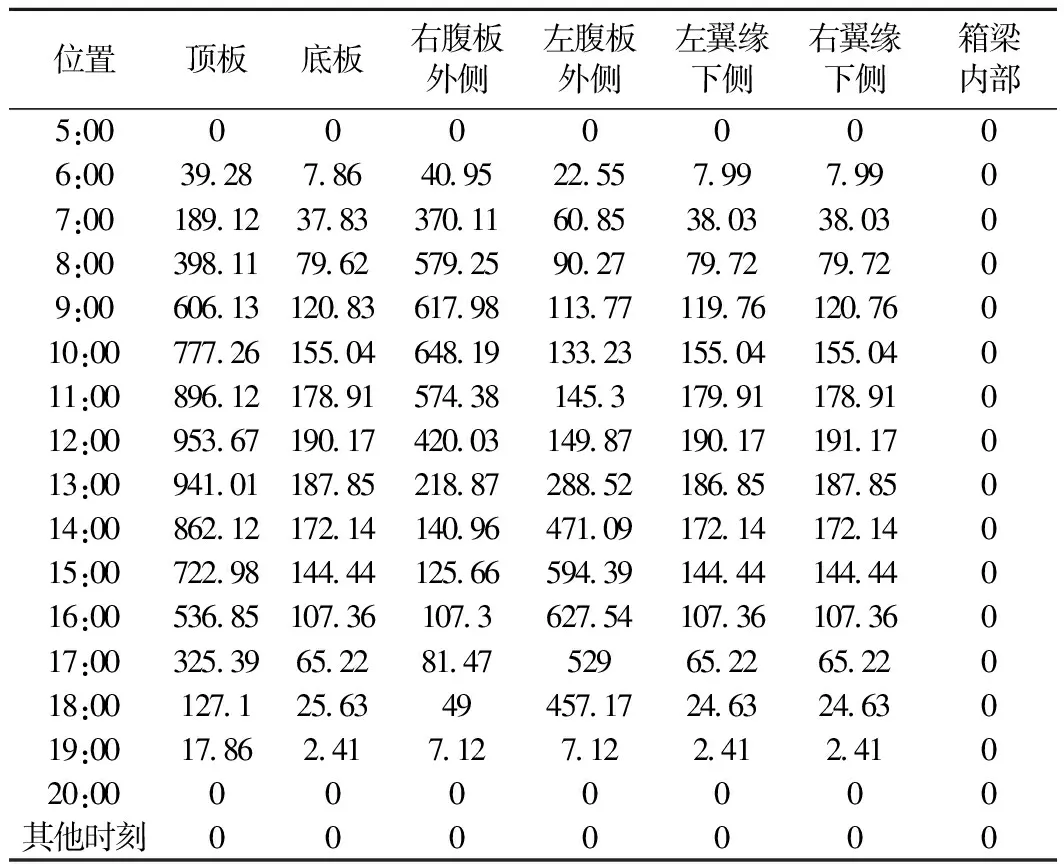
表2 太阳辐射计算结果 W/m2

4 ANSYS有限元计算结果

4.1 不同时刻截面温度云图

基于上述热传递基本原理并结合太阳辐射以及其他气温气象资料，对双室箱梁的温度场进行瞬态分析，得到了箱梁截面一天内的温度变化情况，如图4、图5所示。

图4 箱梁截面温度场分布 (5：00-14：00)

图5 箱梁截面温度场分布 (17：00-02：00)

从不同时刻箱梁截面温度场图像可以看出，从早上开始随着太阳的照射，靠近箱梁表面的温度迅速升高，箱梁内部温度变化相对较缓慢。

4.2 不同节点温度随时间变化曲线

为了探究竖向与横向温度随时间的变化规律，选取右腹板以及底板中线位置的部分节点，N1～N5为竖向节点，N6～N10为横向节点，各选取点的具体位置如图6、图7及表3所示。

对选定节点绘制温度随时间变化的曲线，如图8、图9所示。

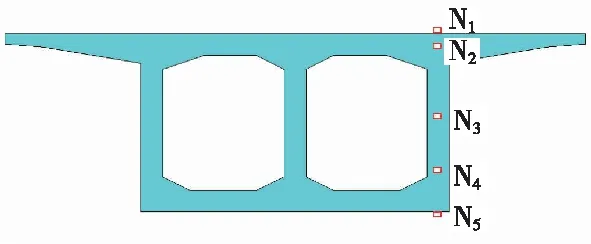
图6 竖向节点选取情况

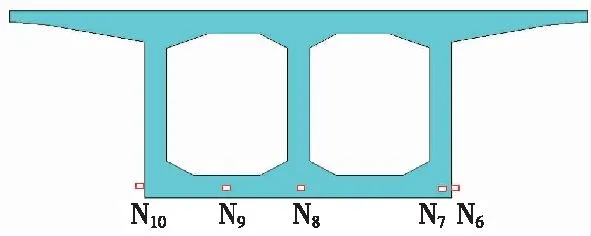
图7 横向节点选取情况

竖向选取节点号与顶板距离/m横向选取节点号与右腹板表面距离/mN10N60N20.200N70.200N31.982N83.350N43.082N95.025N53.882 N106.670

图8 竖向节点温度随时间变化曲线

N1为箱梁顶板位置，N2在顶板下0.2 m的位置，N3与N4位于靠近腹板中部位置，N5在底板表面位置。从图8可以看出，靠近顶板表面的节点温度随时间变化幅度最大，接近25 ℃，在14：00～15：00达到最大值，越往箱梁内部靠近温度变化越缓慢，其达到最大温度的时间也相对较晚；对于位于截面中间位置的节点，其温度随时间变化缓慢且变化幅度较小，约为5 ℃。

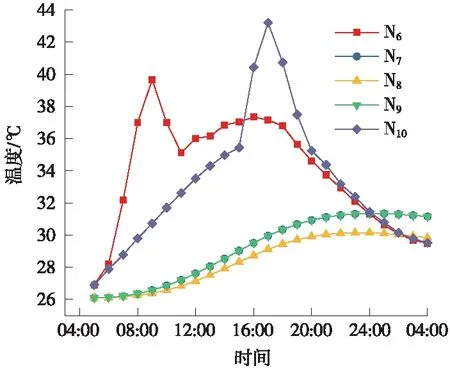
图9 水平节点温度随时间变化曲线

N6是箱梁底板中线最右侧位置节点，N7在距N6左侧0.2 m的位置，N8和N9在中间位置，N10为最左侧位置节点。从图9可以看出，靠近东西两侧腹板表面的节点温度随时间变化幅度大，中间位置节点温度变化相对缓慢且幅度较小，约为5 ℃。

4.3 截面竖向温度分布

通过对箱梁截面温度云图以及右腹板距离底板外表面不同高度节点的温度时程曲线相关数据分析得到，竖向最大温差出现在下午15：00时刻，同时提取3个腹板中线附近节点温度值，得到温度沿截面高度方向的分布曲线，如图10所示。

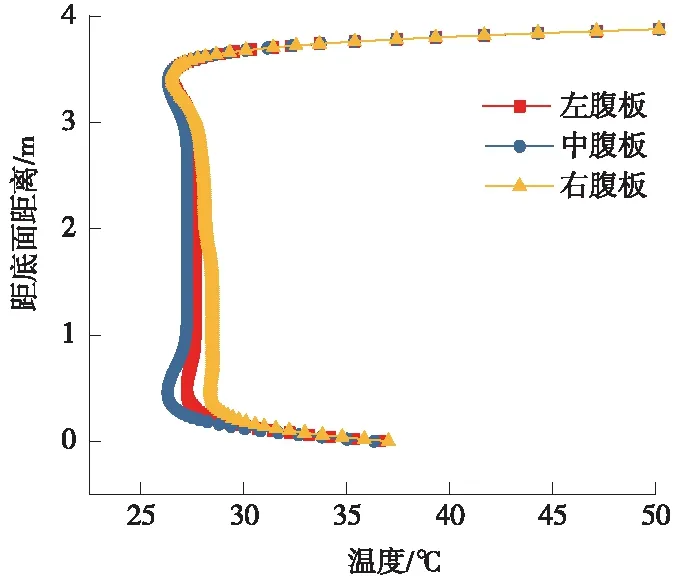
图10 不同腹板中线处温度随位置变化曲线

从图10可以看出，左中右三个腹板温度随高度变化规律基本一致：从顶面向下大约0.4 m范围内温度急剧下降，之后温度基本保持不变，底板附近有来自地面的反射，温度略有升高。中腹板两侧与箱内空气接触，总辐射量为零，顶板上表面受到太阳直接辐射，所以温差最大，在进行最不利温度梯度选取时按照中间腹板的温度梯度分布。

4.4 横向温度分布

从图9可以看出，在上午9：00时刻，由于在此前东面腹板下部一直有太阳照射，而西面没有，此时左右温差最大，通过提取此时底板中部节点进行分析，得到如图11所示的横向温度分布曲线。

图11 底板中线处温度随位置变化曲线

图11中，横坐标表示距右腹板外表面的距离，纵坐标表示温度值，可以看出，在上午9：00时刻底板横向温度从外向内急剧减小，在中间位置基本保持不变，右侧温度最大值远大于左侧最大值。

4.5 我国规范对温度梯度的规定

根据我国现有的《高速磁浮交通设计规范》[7]6.3.26规定：磁浮轨道梁的温度梯度选取宜参照《铁路桥涵钢筋混土和预应力混凝土结构设计规范》[13](TB10002.3—2005)的温差梯度模式，并结合当地试验梁温差实测数据取值。后者规定，对于无砟无枕轨道箱梁温差的计算，应分别考虑沿梁高方向的温差荷载和两个方向的组合温差荷载(图12)。箱梁沿梁高、梁宽的温差分布曲线，按下式计算

Ty=T01·e-ay，Tx=T02·e-ax

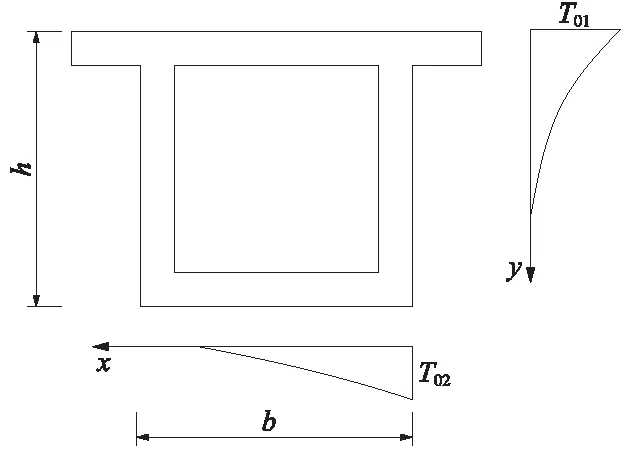
图12 规范中对横向与竖向温差的规定

式中Tx、Ty——计算点x，y处的温差，以℃计；

T01、T02——箱梁梁高或梁宽方向的温差，以℃计；

x，y——计算点至箱梁外表面的距离，以m计；

α——按表4取值。

表4 日照温差a与T0取值。

磁浮轨道梁一般为无砟桥面，根据上述规定，截面竖向与横向的温度梯度分别为：Ty=20·e-5y，Tx=16·e-7x。

从图10与图11中竖向与横向温度分布情况可以看出，得到的温度梯度分布模式与规范不完全符合，主要表现在不是向一侧单调减小。为了更好拟合这种温度分布情况，参照国内外相关文献，大多数规范对升温温度梯度选取时并未考虑靠近下表面边缘温度有局部增大的情况，新西兰规范对此考虑的方法是：在箱梁顶部向下1.2 m范围内与底板表面向上0.2 m分别施加不同的温度梯度荷载[14]。此形式与本文中ANSYS有限元模拟得到的温度分布情况类似，结合《铁路桥涵钢筋混凝土和预应力混土结构设计规范》[13]中采用的指数温度模式，从顶面向下1.2 m的范围内采用指数函数拟合，得到在此范围内温度梯度T=24.98×e-9.07y；由底板表面向上0.4 m后内温度基本稳定，对此范围节点采用指数拟合，得到在此范围内的温度梯度表达式为：T=10.48×e-9.13y。同样地，对底板横向温度梯度采用相同的方式进行拟合，选取此左右外表面分别向内0.3 m节点温度值进行拟合，温度梯度表达式分别为T=13.8×e-12.8x，T=4.5×e-11.4x′，其中y表示到上顶面的距离，y′表示距下底面的距离，x表示距右腹板外侧的距离，x′表示与左腹板外侧的距离。图13、图14分别为竖向与横向温度梯度拟合情况简图。

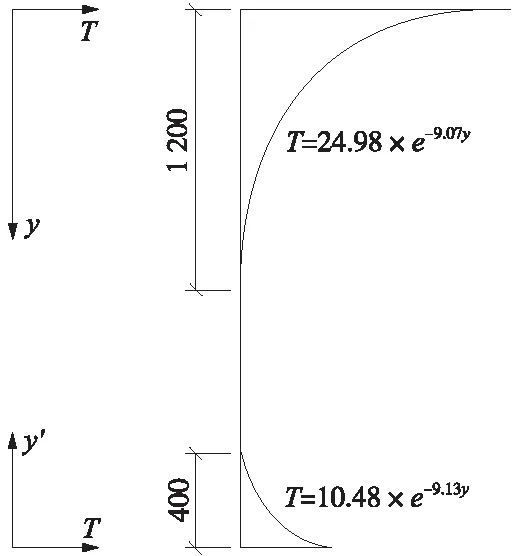
图13 竖向温度梯度模式(单位：mm)

图14 横向温度梯度模式(单位：mm)

5 结论

以上海地区的某双室箱梁为例，结合上海夏季气候特征，利用ANSYS有限元软件，研究了不同单箱双室混凝土截面在太阳照射下的温度分布情况，得到以下结论。

(1)混凝土箱梁在日照条件下截面温度从外表面向箱梁内部温度急剧下降，靠近箱梁中部温度基本不变，混凝土外表面温度与气温变化规律基本相同，靠近箱梁内部温度变化很小，且温度峰值与气温变化相比有一定滞后性，表明混凝土是热的不良导体，截面的温度梯度很大。

(2)双室箱梁不同腹板沿高度方向温度分布形式基本相同，从顶板表面向下存在很大的温度梯度，顶底板之间的位置温度基本不变，靠近底板附近温度有一定回升。

(3)通过指数函数对横向与竖向温度梯度拟合表明：双室箱梁温度梯度与规范值不一致，竖向温度梯度峰值比规范值大，横向温度梯度峰值比规范值小，二者变化均比规范值要剧烈，二者在另一侧均存在一定的反向温差。

(4)对于全国不同地区的温度梯度模式选取，应结合当地气候特征以及现场实测数据，可以保证温度梯度的选取更加合理。