让课堂教学顺应学生的思维生长——执教《小数乘小数》

江苏省南京市民办实验学校 郭大萍

【案例背景】

本课重点探索小数乘小数的计算方法，是在学生了解了小数乘法的意义、小数点的移动引起小数大小变化的规律以及初步讨论了积的小数位数与乘数小数位数的关系（小数与整数相乘）的基础上进行教学的。教材提供了一个关于小明房间和外面阳台平面图的情境，如下图：

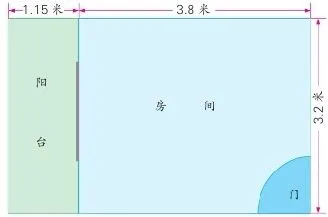
相关信息是：房间长3.8米、宽3.2米；阳台长3.2米、宽1.15米。求房间和外面阳台的面积各是多少平方米？通过这样一个情境，组织学生探索小数乘小数的一般计算方法，即先将小数乘法转化成整数乘法进行计算，再根据乘数扩大的倍数，将乘积缩小相同的倍数，以此让学生体会到乘数共有几位小数，积就有几位小数。重点是理解把小数乘法转化成整数乘法后，得到的积回归小数乘法积的推理过程。

【案例描述】

一、找准思维的起点

1．由转化到回归

师：同学们还记得我们是怎样推导出平行四边形、三角形和梯形的面积计算公式的吗？顺势出示如下的三组图片：

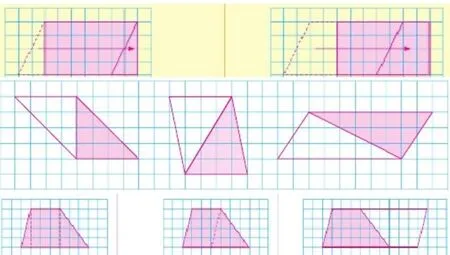
生1：我们将平行四边形转化成了长方形，将三角形和梯形转化成了平行四边形，从而分别得到了这三种图形的面积求解公式。

师：这位同学提到了一个词——“转化”：我们将未知图形转化成已经学习过的图形，再根据已经学习过的图形与未知图形的关系，将已知图形的面积计算方法回归到对未知图形的面积推导中去，转化后再回归是一种重要的思维方法，今天这节课我们还会用到它。

2．整数乘法

教师板书两道习题，要求学生用竖式进行计算，并选择四名学生板演，然后集体交流下面的问题：计算整数乘法如何摆竖式？在计算的过程中要注意什么？

38×32；32×115。

生2：计算小数乘法时要注意末尾对齐，计算时要明白其中的道理，要细心，算完后还要验算一下。

二、注重思维的过程

1．提出问题

师：小明想了解一下自己的卧室有多大，他进行了测量。我们一起去看看吧！（课件出示）

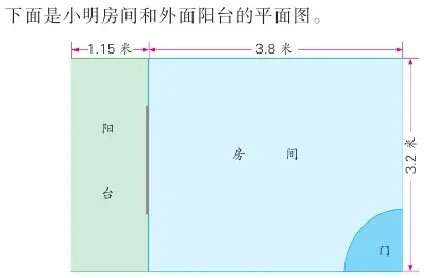
师：从题目中，你发现了什么数学信息？你能提出什么数学问题？

生1：小明的卧室是长方形的，分为房间和阳台两部分，房间和阳台也都是长方形的，房间长3.8米、宽3.2米；阳台长3.2米、宽1.15米。

生2：房间的面积是多少平方米？

生3：阳台的面积是多少平方米？

生4：卧室的总面积是多少平方米？

……

师（根据学生的发言，列举出所有的问题）：同学们都很善于思考，我们选择其中的两个问题来研究吧！（将“房间的面积是多少平方米”和“阳台的面积是多少平方米？”这两个问题展示出来）

2．探索方法

师：我们先来解决“房间的面积是多少平方米”这个问题，你会列式计算吗？（生发言，师板书：3.8×3.2=）

师：观察算式，它和我们之前学习的小数乘法相同吗？

生5：不同。

师：哪里不同？

生6：以前学习的是小数同整数相乘，这道题是小数乘小数。

师：是的，这就是今天要研究的主要内容。（板书课题：小数乘小数）

师：根据大家的经验，你能估算出房间的面积吗？

生7：把3.8看成4,4×3.2=12.8（平方米）。这样把一个乘数看大了，实际上不会超过13平方米。

生8：把3.2看成3,3.8×3=11.4（平方米）。这样又把一个乘数看小了，实际上肯定超过11平方米。

生9：也可以把3.8看成4，把3.2看成3,4×3=12（平方米）。一个乘数看大了，另一个乘数又看小了，结果应该比较接近准确值了。

师：同学们用不同的方法对小明房间的面积做了估计，可以确定面积在11平方米到13平方米之间。

【案例分析】

在数学这门学科里，很多新知识往往是旧知识的引申、发展和综合，而学生的认知活动也总是以已有知识和经验为前提的，因此，数学教学活动必须建立在学生已有知识经验的基础上。教学时，教师要根据知识间的内在联系，找准学生思维的起点，并以此为突破口引导学生利用知识的迁移规律主动地获取知识。对于本节课，我有如下思考：

1．突出转化的思想，注重学生自主构建方法

学生思维的起点建立在已有知识的基础上。小数乘小数与整数乘法联系密切，尤其是在计算方法上，两者有着内在的联系。唤醒学生对“转化”思想方法的认知和让学生列竖式计算整数乘法有利于学生理解小数乘小数的算理，也有利于计算方法的有效迁移。

2．多种计算方法互融，培养学生良好的计算品质

本节课以笔算为主，同时也穿插着口算、估算。对于教师给出的情境图中的两个问题，每一次计算前，教师都要让学生先估一估，培养学生“先估算、后计算”的好习惯，引导学生将最终的结果与自己估算的结果进行比较，又培养了学生用估算来判断结果的合理性与正确性的好习惯。口算和估算以笔算为基础，笔算又是口算和估算的一种应用。口算是在学生掌握了笔算方法后进行的，这也为接下来练习课中让学生直接写出得数和直接比大小做好了铺垫。对于计算教学来说，重视培养学生口算、估算的习惯有利于笔算教学的顺利进行，也有利于培养学生良好的计算品质和反思能力。