解析几何中巧用圆锥曲线定义解题的探索

江苏省宜兴第一中学 张郡麟

定义是揭示事物本质属性的思想形式，面对一个数学对象，回顾它的定义，常常是解决问题的锐利武器。圆锥曲线的第二定义体现了“形”的统一，第一定义则体现了“质”的区别，两种定义不仅在解题中应用广泛，而且具有很大的灵活性。第一种定义和第二种定义的灵活转换常常是打开解析几何问题思路的钥匙，在题目中挖掘这些隐含信息有助于解题。下面我们一起来看看圆锥“定义”在求解圆锥曲线问题中有哪些常规应用。

分析：本题的解题关键在于巧用椭圆的第一定义，首先解出椭圆的长半轴长a，然后利用勾股定理求出半焦距c，从而构建出椭圆方程。

【例题2】（1）一动圆与圆x2+y2=1外切，而与圆x2+y2－6x+8=0内切，那么动圆的圆心轨迹是什么？（2）已知点M(－3，0)，N(3，0)，B(1，0)，⊙O与MN相切于点B，过M，N与⊙O相切的两直线相交于点P，则P点的轨迹方程为__________。

解答：（1）已知圆x2+y2=1的圆心为O(0，0)，半径为r1=1，

圆x2+y2－6x+8=0的圆心为A(3，0)，半径为r2=1。

设动圆的圆心为P，半径为r，则|PO|=1+r，|PA|=r－1，

则有|PO|－|PA|=2＜|OA|=3，所以动圆的圆心轨迹为双曲线的一支。

（2）|PM|－ |PN|=|PA|+|AM|－ |PC|－ |CN|=|MA|－|NC|=|MB|－|NB|=4－ 2=2。

∴P点的轨迹是以M，N为焦点的双曲线的右支，c=3，a=1，b2=8。

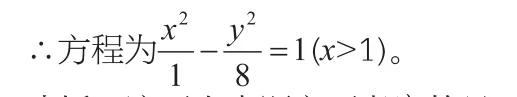
分析：这两个小题主要考察的是双曲线的第一定义，构造出两个相减后等于一个常数的点点距离，然后注意到与双曲线定义的不同点，得出所求轨迹只能是双曲线的一支。

【例题3】设F1、F2是双曲线x2－y2=4的左、右两个焦点，P是双曲线上任意一点，过F1作∠F1PF2的平分线的垂线，垂足为M，求点M的轨迹方程。

分析：一般情况下，距离之和有什么最值？距离之差有什么最值？现在要求PA+PF的最大值，那我们可以怎么转化呢？首先利用椭圆的定义转化为距离之差，PA+PF=PA+(2a-PF1)，其中F1为椭圆左焦点，然后将PA+(2a-PF1)写成2a+(PA-PF1)，最后利用数形结合法“三点共线”来确定所求P点即为AF1的延长线与椭圆的交点。

我们在解有关圆锥曲线的问题时，如果题目涉及焦点、准线方程、离心率、圆锥曲线上的点这四个条件中的三个，我们一般就要联想到圆锥曲线定义，有时甚至只要知道其中的两个条件，也可以联想到圆锥曲线定义。灵活巧妙地运用圆锥曲线的定义，将会带给我们意想不到的方便和简单。圆锥曲线的定义反映了它们的基本特征，理解定义是掌握其性质的基础。因此，对于圆锥曲线的定义不仅要熟记，还要深入理解细节部分，比如椭圆的定义中要求|PF1|+|PF2|＞|F1F2|，双曲线的定义中要求||PF1|-|PF2||＜|F1F2|。这样，在解题过程中才不会步入歧途。