巧借构造法 妙解数学题——解析构造法在高中数学解题中的应用

山东省青岛市城阳第三高级中学 李朝磊

构造法是一种简便的解题方法，但其对学生的数学水平及综合素质要求较高，因此，教学实践中，教师应结合不同题型讲解构造法的具体应用，使学生明晰构造法的应用步骤，把握应用构造法解题的重点与难点，迅速正确解答相关数学题目。

一、构造方程

学生对方程知识较为熟悉，在解答一些数学试题时，通过分析题干条件，构造方程求解可获得事半功倍的解题效果，因此，教学实践中，教师应有针对性地对学生加以引导，提高学生应用构造方程解题的意识，培养学生应用构造方程的习惯，促进学生数学解题能力的进一步提高。

例1 已知α+β+γ=π，试证明：

（1）sin2β+sin2γ-2sinβsinγcosα=sin2α；

（2）cos2β+cos2γ+2cosβcosγcosα=sin2α。

分析：该题目已知条件较少，部分学生应用三角函数知识进行变换，虽然能够得出证明结果，但计算过程烦琐，出错率较高，如构造方程，可明显降低证明复杂度，具体解题过程为：

证明：设x=sin2β+sin2γ-2sinβsinγcosα-sin2α①

y=cos2β+cos2γ+2cosβcosγcosα-sin2α②

① + ② 得：x+y=2+2cosαcos（β+γ）-2sin2α=2（1-sin2α）+2cosαcos（π-α）=2cos2α-2cos2α=0。

同理，② - ①得：y-x=cos2β+cos2γ+2cosαcos（β-γ）=-2cosαcos（β-γ）+2cosαcos（β-γ）=0。

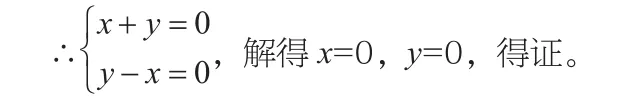
构造方程解答数学题目的技巧性较强，教学实践中，教师除了讲解相关题目外，还应对学生多加训练，鼓励学生总结构造方程的适用条件、解题规律，确保构造的方程科学、合理。

二、构造函数

众所周知，高中数学试题复杂多变，难度相差较大，部分题目无从下手时，可考虑适当的构造函数，利用函数图形、性质进行求解。实践表明，构造函数可迅速找到解题突破口，迅速得出正确结果，因此，教学实践中，教师应注重讲解构造函数在解题中的具体应用。

例2 已知关于x的方程x2-（2a+1）sin（cosx）+1-4a2=0有唯一实数解，求实数a的所有取值。

分析：该方程为二次方程，但存在特殊的参数，很多学生面对该题目时不知如何下手。事实上，认真观察给出的方程，通过构造函数，便可“柳暗花明”。教学实践中，教师可详细列出解题过程，要求学生认真思考，感受构造函数法的具体应用，以更好地应用到其他题目解答中。

解：构造函数f（x）=x2-（2a+1）sin（cosx）+1-4a2，

∵f（-x）=f（x），∴f（x）为偶函数。

设x0为f（x）=0的解，则-x0也为f（x）=0的解。

由题干可知f（x）=0有唯一的实数解，即-x0=x0，显然，x0=0。

通过该例题讲解，学生可充分感受到构造函数在解答数学题目中的便捷、巧妙之处，因此，教学实践中，教师应深入讲解函数知识，使学生夯实函数知识，为构造函数法的灵活应用做好铺垫。

三、构造图形

解答数学题目时，通过构造相关图形，将参数间的关系通过图形直观地加以呈现，不仅有助于提高解题效率，而且还可加深学生对数学题目的深入理解，因此，教学实践中，教师应引导学生认真分析题干已知条件，找到已知条件与图形的契合点，学会运用图形解答数学试题。

例3 已知a＞0，b＞0，a+b=1，

分析：面对该题目，很多学生不知所措，甚至教师提示使用构造图形进行证明时，仍找不到解题突破口。因此，解答该题目时，教师做好充分的引导显得尤为重要，即要求学生认真观察给出的已知条件以及要证明的结论，找到条件和结论间的联系。由已知条件可知a+b=1，不难联想到=2，如此便和结论联系在了一起。具体解题过程为：

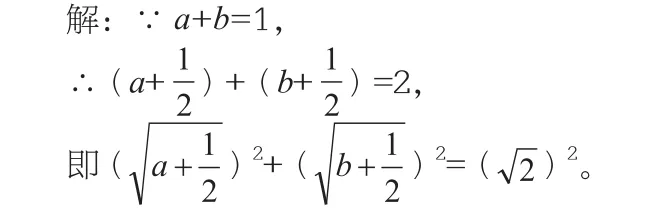
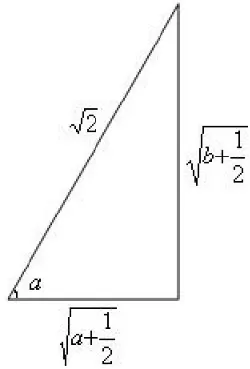
由平方和可以联想到勾股定理，即构造如右图的三角形：

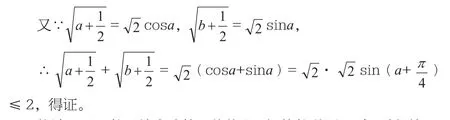
构造图形是数形结合法的具体体现，解答数学题目时，过程简明、清晰，计算简单，较传统方法优势明显，因此，解答数学题目时，教师应引导学生学会联想，构造熟悉的数学图形辅助解题。

为提高学生的数学解题能力，掌握正确的解题方法尤为关键，其中构造法是一种重要的解题方法，在解答高中数学试题中应用普遍，因此，教学实践中，广大教师应提高认识，注重构造法知识的讲解，尤其是依托具体案例，讲解构造法在解题中的具体应用，包括构造方程、构造函数、构造图形等，使学生掌握构造法的应用技巧，巧妙解答相关数学试题。