巧用柯西不等式解题

湖北省黄冈市麻城市第一中学 卢红玲

柯西不等式，最初来源于数学家柯西，他在研究流数问题时分析得到了从此闻名于世的柯西不等式，而后又经过其他数学家的不断推广和完善，逐步形成了今日我们所学习的内容，如今已经被纳入新课程选修教材的教学内容《不等式选讲》。

一、合理搭配

二、构建因式

柯西不等式的结构十分简单直观，由两个部分组成，不等号的一边是因数相乘的形式，另一边则是完全平方。但一般出现的题型中有些没有这两个柯西不等式的明显标志，比如说需要证明的不等式左右两边都没有出现乘积或是完全平方的形式，许多同学由于对知识掌握不够熟练、缺乏解题经验，不容易联想到用柯西不等式去解题。此时我们可以在不等号某一边自行构建一个因式或完全平方，让它与柯西不等式的结构相符，从而套用柯西不等式来解题。

例2：设a+b∈R+，a+b=1，请证明

分析：本题中并没有出现柯西不等式的标志，而且需要证明的式子含有a和b的八次方项，条件中仅给出了一次方项。这里就需要构建因式，巧用这个条件，将结论部分转化为只要证明这个不等式就可以了，但目前离题目给出的条件还有一定距离，所以我们需要连续运用多次柯西不等式。

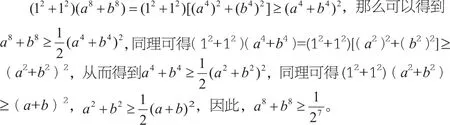
点评：刚接触到这种类型题目的同学可能会觉得有些难度，不容易联想到柯西不等式，或是不知道如何巧妙地构建因式来解题。我们总结了这一类题型，同学们可以记住这样的结论：“当时，有；当，有，以便更好地理清解题思路，掌握举一反三的能力。另外，这道题的应用很好地体现了柯西不等式的降次能力，利用三次柯西不等式，将结论左边的八次方项成功降次。

三、调整结构

这一类题目依旧是不具备明显的柯西不等式的标志，我们可以将已知结构进行适当的调整，使之符合柯西不等式的一般架构。

点评：联系不等式两边，适当对不等式进行变形，使其可以应用柯西不等式。

在高中试题中，除了以上提到的四种变形方法，还有一些其他的小技巧，这里不一一例举。此外，学生们可能还会遇到更加复杂的一些不等式问题，涉及以上几种技巧的组合，又或是关联到其他数学知识，如基本不等式等。归根结底，这类问题的关键还是在于如何建立题目所给条件与所求结论之间的联系，只要把握好这一重点，以往我们望而却步的难题将迎刃而解。