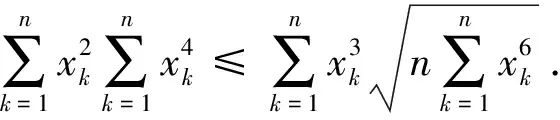数学问题解答

2018年12月号问题解答

(解答由问题提供人给出)

2456已知a1,a2,…,an>0(n≥2)，求证：

(浙江省海盐县元济高级中学 张艳宗 314300；北京航空航天大学图书馆 宋庆 100191)

证明由柯西不等式，

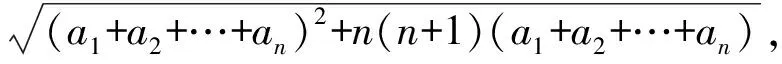
从而由均值不等式

≥n(n+1).

即证．

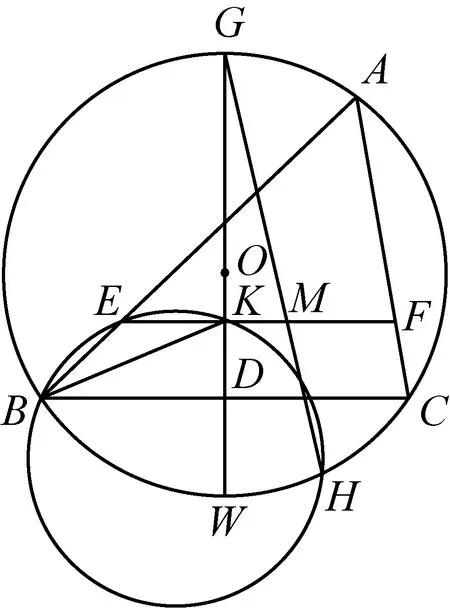
2457如图，E、F分别在△ABC的AB、AC上，且EF∥BC，过BC中点D作DG⊥BC交△ABC的外接圆O于G和W，交EF于K，△BEK的外接圆交⊙O于H，GH交EF于M，求证：A、M、W三点共线.

(江西师范高等专科学校 王建荣 335000)

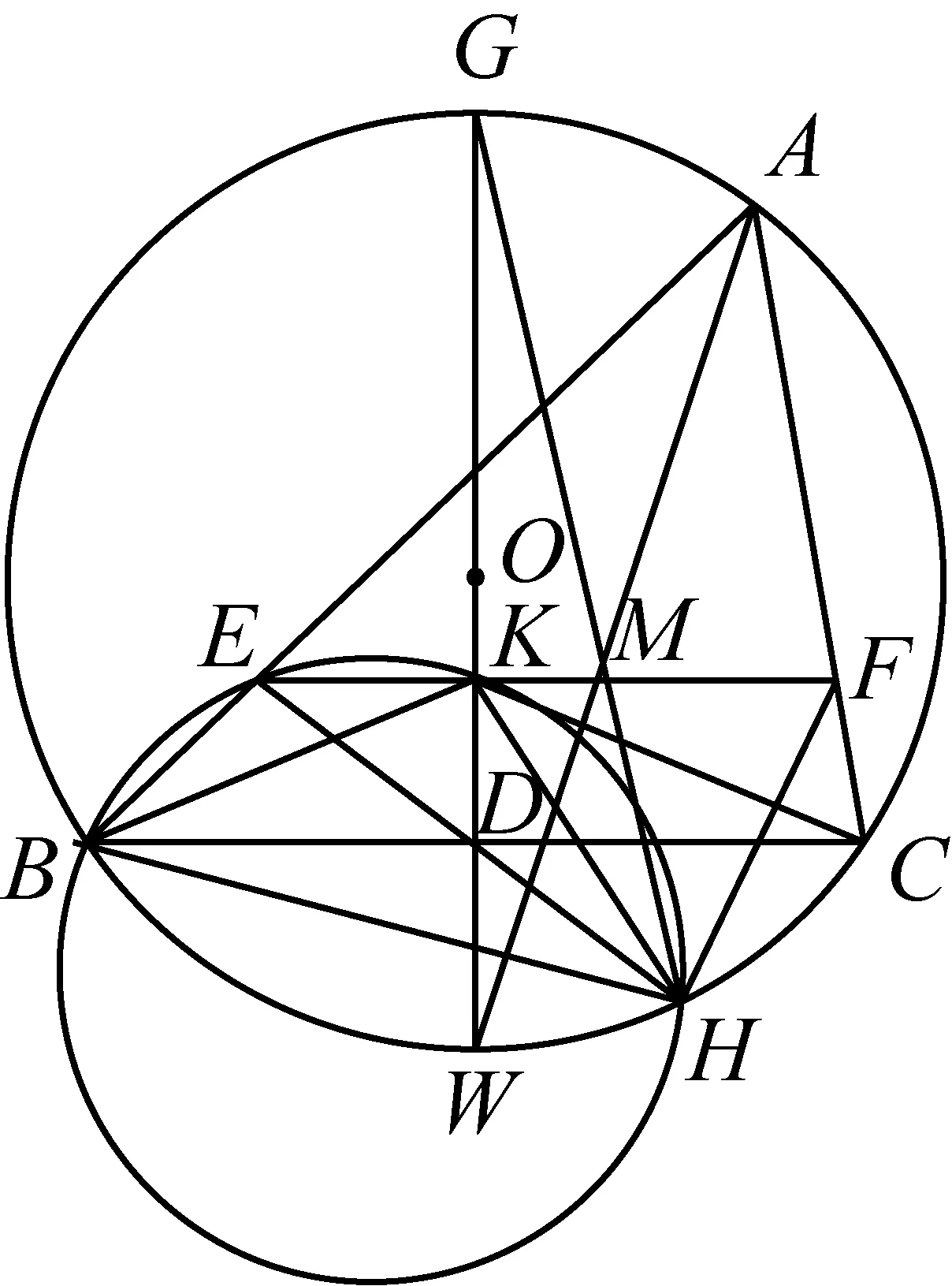
证明连KH、BH、CH、EH、FH、KC、AM，如图，由∠EKH+∠ABH=∠ACH+∠ABH=180°⟹K、H、C、F共圆，由于GD为BC的垂直平分线⟹∠BHG=∠CHG、KB=KC、∠EKB=∠FKC⟹∠EHB=∠FHC，

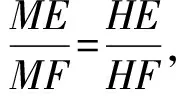
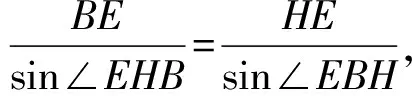
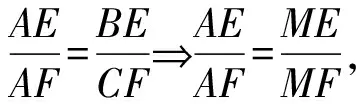
故AM平分∠BAC，

因此AM一定通过W．

2458在△ABC中,求证

(1)

(天津水运高级技工学校 黄兆麟 300456)

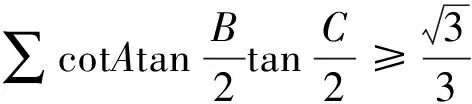
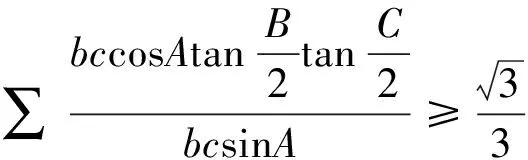
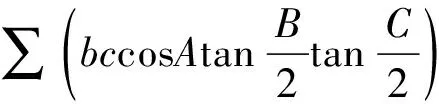
(2)

其中Δ为三角形的面积.

为了证明与待证不等式(1)等价的不等式(2),可转证比(2)更强的如下不等式(3)

(3)

设不等式(3)左右之差为M,由不等式(3)的全对称性,不妨设a≥b≥c,

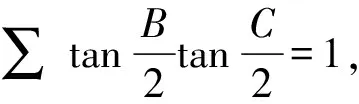
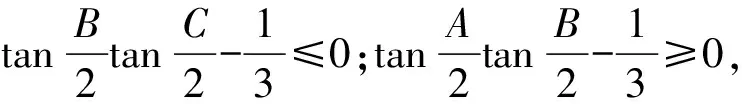
且还有bccosA≤cacosB≤abcosC,

那么有

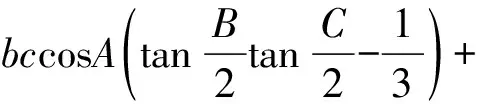
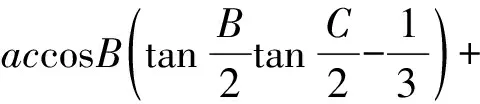
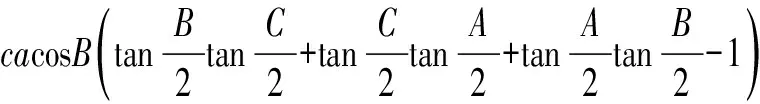
=0,

故知不等式(3)成立.另一方面由余弦定理及外森比克不等式,可得

联立不等式(3)及传递性,立得不等式(2),从而知不等式(1)成立.

2459设点I,Ia,Ib,Ic分别为△ABC的内心和旁心，R为其外接圆的半径，证明：6R≥IIa+IIb+IIc.

(安徽省枞阳县宏实中学 江保兵 246700)

图1

证明设△ABC内切圆的半径为r，p,s分别为其半周长和面积,ra,rb,rc为旁切圆半径，由内心和旁心的性质，I,B,Ia,C四点共圆，且这个圆的直径为IIa，如图1所示.由正弦定理：

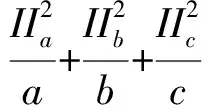
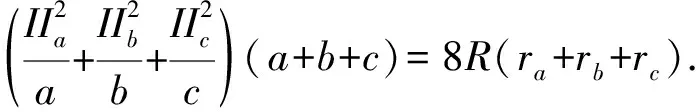
一方面，由柯西不等式

另一方面

这里应用了三角恒等式

这里应用了三角恒等式

ra+rb+rc-r

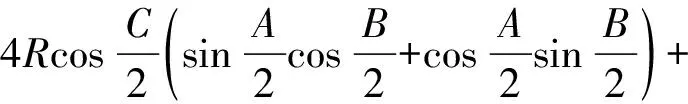
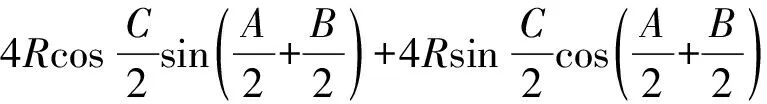
=4R，

即ra+rb+rc=4R+r，

8R(ra+rb+rc)=4R(8R+2r)≤36R2，

这里应用了欧拉不等式R≥2r.

综上我们有

36R2≥8R(ra+rb+rc)

≥(IIa+IIb+IIc)2，

即6R≥IIa+IIb+IIc(当且仅当三角形△ABC为正三角形时等号成立).

2460在三角形ABC中，记BC=a,CA=b,AB=c，n∈N+且n≥2，0<λ≤1，求证：

(安徽省岳西中学 储百六 246600)

证明先证一不等式：当x∈0,1时，

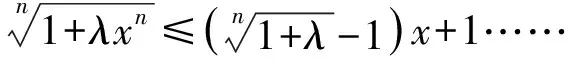
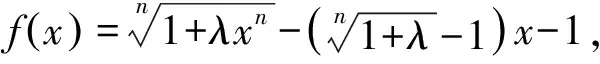
x∈0,1，则

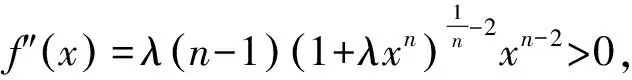
所以f′x在0,1上为增函数；

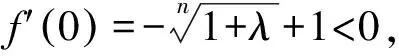
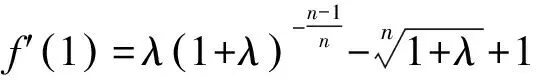
所以存在x0∈0,1，使得f′x0=0，于是

当0

当x>x0时，f′x>0；

所以fx在0,x0上为减函数，

在x0,1上为增函数,

所以当x∈[0,1]时，

f(x)≤max{f(0),f(1)}=0，

故①成立.

因为是对称不等式，不妨设a≥b≥c>0，

于是由①可得

由此有

又因为

所以

2019年1月号问题

(来稿请注明出处——编者)

(湖北省谷城县第三中学 贺 斌 龚为民 441700)

2462已知如图，AB为⊙O的直径，弦CD⊥AB于点E.点M1、M2在OC上，且CM1=OM2.直线AM1、AM2分别交⊙O于点N1、N2.求证：

S△DCN1·S△DCN2=S△DBN1·S△DBN2.

(北京市芳草地国际学校富力分校 郭文征 郭璋 100121)

2463设a,b,c>0,求证：

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000 )

2464△ABC的内切圆O分别与边BC、CA相切于D、E，连AD，AD与圆O又交于P，连BP，CP.求证：BPC=90°的充要条件是AE+AP=PD.

(江苏无锡市第一中学 李广修 214031)

(山东省滨州市北镇中学 宋志敏 256600)