数学问题2313号引致的一条不等式链
2019-03-08 06:53:44何灯
数学通报 2019年1期
何 灯
(福建省福清第三中学 350315)
设△ABC的3条边长为a,b,c,其内切圆半径、半周长、面积分别为r、s、S.对应边上的旁切圆半径、高线、角平分线、中线长分别为ra、rb、rc;ha、hb、hc;wa、wb、wc;ma、mb、mc.
2016年第7期《数学通报》中的2313号问题:
(1)
文[1]中得到和式(1)类似的如下三个不等式.
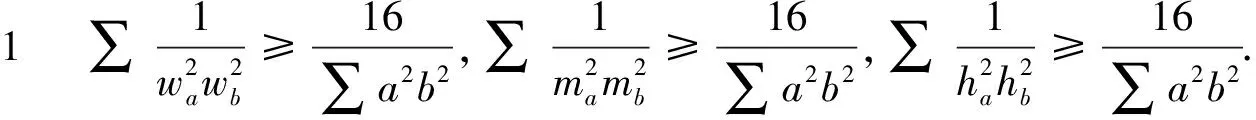
更一般地,文[1]中建立了定理1的指数推广形式.
定理2对于n∈N+且n≥2,有
评注1根据文[1]中定理2的证明过程,条件n∈N+可略去,即定理2对不小于2的实数n均成立.
读罢文[1],笔者感触颇深,不禁联想到与之相关的几篇文章.
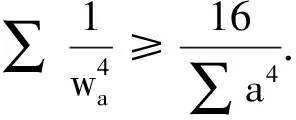
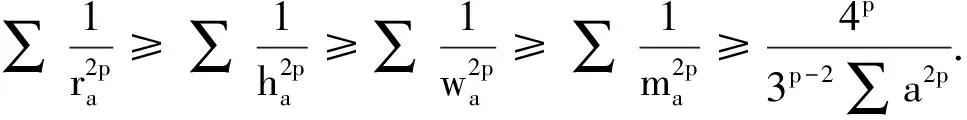
(2)
受定理2、3的启发,笔者思考能否将两个定理中的不等式进行串联,以进一步揭示它们之间的联系.经探究,得到如下结论:
定理4设p≥2,则
证明据定理2、3,只需证明
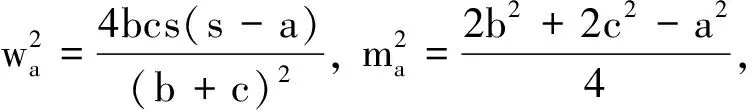
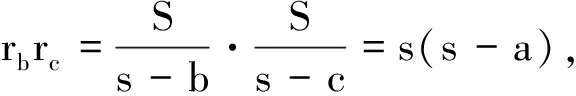
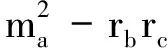
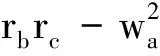

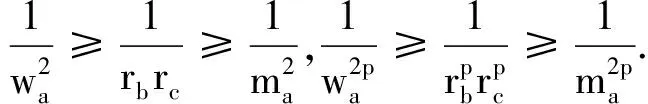
同理可得
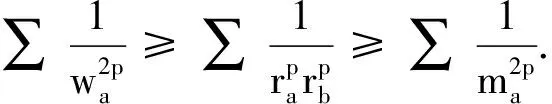
由熟知的不等式∑x2≥∑xy(x,y,z>0),
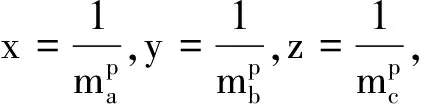
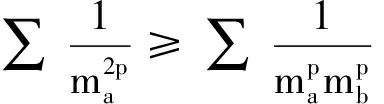
综上,定理4成立.
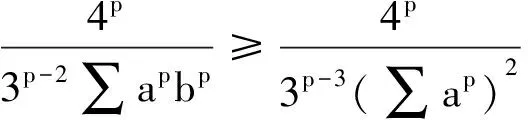
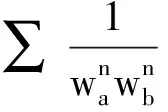
猜你喜欢
数理天地(高中版)(2022年19期)2022-05-30 10:48:04
中等数学(2021年2期)2021-07-22 06:21:52
中等数学(2020年9期)2020-11-26 08:07:28
郑州大学学报(理学版)(2020年1期)2020-02-08 08:40:00
中学生数理化(高中版.高考数学)(2019年9期)2019-11-27 20:09:58
Chinese Medical Sciences Journal(2019年1期)2019-04-11 09:26:46
中等数学(2018年7期)2018-11-10 03:29:04
中学数学杂志(高中版)(2018年1期)2018-01-27 18:49:49
中等数学(2017年1期)2017-06-01 12:21:50
上海金属(2016年2期)2016-11-23 05:34:23

