合理设计教学过程 发展学生核心素养
——以“零指数幂、负指数幂”为例
石志群
(江苏省泰州市教研室 225300)
新一轮课程改革提出了“核心素养”的概念和中国学生核心素养的基本框架与内容,各学科也据此明确了学科核心素养的具体内容,普通高中数学课程标准提出了“数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析”六大核心素养,并在“课程性质”中提出了“提升学生的数学素养,引导学生会用数学眼光观察世界,会用数学思维分析世界,会用数学语言表达世界”的观点.笔者认为,“用数学眼光观察世界、用数学思维分析世界、用数学语言表达世界”既是数学核心素养的表现形式,更是发展学生数学素养的基本路径.也就是说,要发展学生的数学素养,特别是数学核心素养,在数学教学过程中就必须引导学生用数学眼光观察世界、用数学思维分析世界、用数学语言表达世界.
下面以“零指数幂、负指数幂”为例,谈谈笔者对基于发展学生核心素养进行数学教学设计及其思考.
1 一个案例
1.1 用数学的眼光看世界
课程标准中对“用数学的眼光观察世界”中的“世界”是有明确的定位的,也就是“发现问题、提出问题”中“问题的来源”,指:现实世界中的、科学中的、数学中的问题.换句话说,“用数学的眼光观察世界”就是指用数学眼光观察现实世界(自然的、社会的)、用数学眼光观察科学世界(自然科学、社会科学)、用数学眼光观察数学世界(数学内部的问题、规律、关系等).
由于零指数幂、负指数幂是正整数幂的推广,可用下面的方法直接提出问题:
前面我们学习了同底数幂相除的运算性质:
aman=am-n(a≠0,m,n是正整数,m>n),
为什么要规定m>n?
学生可以想到:可以考察如果m不大于n,即m≤n,会出现什么情况:
若m=n,那么就会出现a0,如果m 师:为什么不允许呢? 生:因为an的意义是n个a相乘的积,0个a相乘、-1个a相乘是没有意义的! 师:很好!下面请大家再考虑一下:当m≤n时,aman是不是就不好运算呢?比如,2323,2324? 师:从上述过程可以看到,要解决同底数幂的除法运算法则在m≤n时能否运用的问题,可以归结为如何解决“0个a相乘没有意义、-1个a相乘没有意义”等问题. 为了解决提出的问题,需要运用数学思维进行分析.而归纳特例、回到原点、直观想象都是数学思维的重要形式. 师:请大家考察一个与乘方有关的实际问题: 1个细胞分裂1次变为2个,分裂2次变为22个,分裂3次变为23个,分裂4次变为24个,…… 当这个细胞没有分裂(即分裂次数为0)时,细胞的个数是多少? 生:还是1个.噢,这说明20=1还是有道理的! 师:那我们怎么办? 生:规定 20=1. 师:非常好!这说明只要将乘方的概念加以推广,20就可以有意义了,从而同底数幂除法运算的法则在m=n时也就可以成立了! 请大家再思考一下,2-1是否有意义呢? (停顿片刻) 大家可以先用数轴进行分析,在数轴上依次标出24,23,22,21,20所表示的点,并研究这些点之间的关系. (学生思考) 生:从图中可以看出,指数每减少1,幂所对应的点为原点与前一个点的中点. 师:按照这个趋势,如果2-1有意义的话,那么它所对应的点应该在哪里?对应的实数是哪个? 生:…… 师:根据正整数指数幂的意义,如果2n=x,那么,2n+1应该是多少? 生:2x. 师:那么,上述猜想的结果是否应该也满足这样的特性呢? 生:应该……是的,真的也满足. 师:既然如此,一般地,2-n(n为正整数)应该是多少呢? 生:…… 师:下面请大家用数学语言对20,2-1,以及一般地2-n(n是正整数)下定义. 师:那么a-n(a≠0)呢? (板书相关规定) 最后说明: aman=am-n(a≠0,m,n是整数) 成立. 思考: am×an=am+n(a≠0,m,n是整数) 是否成立?同底数幂的乘法运算法则与除法运算法则之间有着怎样的关系? 这是一节课题研究型的数学建构课,从学生已有知识结构出发,运用数学的眼光发现问题(事实上,历史上的数学家们也就是这样发现问题、发展数学的,或者说,这就是数学研究的基本过程):为什么同底数幂的除法运算法则中要作m>n的规定?进而通过数学的思考,将其归结为零指数幂、负指数幂有没有意义这个核心问题(或中心问题).先让学生由乘方的意义(原始意义)发现它没有意义(正因为其没有意义,我们才有资格对其进行新的定义),再通过数学的思维进行分析,从而发现其新的意义,进而引入零指数幂和负指数幂的概念. 本课,学生经历了数学探究的完整过程: 从原运算法则的“不能”,思考“为什么不能?”通过数学分析,寻找零指数幂、负指数幂的新的意义,从而拓展了乘方运算的意义,而这种“新”的意义又保持了正整数指数幂所具有的相互关系.这样的过程,充分体现了拓展新概念的必要性、合理性,又渗透了数学的统一美,让学生感受到数学的理性精神和价值理念.同时,这为将来将整数指数幂推广到分数指数幂打下了思想与观念的基础(其推广的方法可以完全类似于此). 从教学的视角看,“用数学眼光观察世界”就是发现问题,“用数学思维分析世界”是解决问题(用数学的知识、方法、思想、观念等),而“用数学的语言表达世界”则是将解决问题的结果(有时也包括过程)用数学的语言(符号、图形以及必要的文字)表达出来,得到数学的模型.这是一次数学的“再发现”过程,学生经历的是一次真正的数学活动. 这个学习过程对于初中学生而言是完全可以胜任的,符合学习的最近发展区理论.这是因为在学习过程中教师充分发挥了主导作用,适时地给学生以帮助、支持,为其数学思维提供“脚手架”. 通过上述案例,笔者认为,数学核心素养的培养应该寓于我们平时的每一节课的教学过程之中,寓于教学的每个环节的精心设计.这种设计既要符合数学的发展规律和内在联系,还要符合数学的研究规范,更要符合学生的认知规律和心理倾向,绝对不能让教师的“权威”替代了数学的理性:数学中的“规定”不是那么随意的,它需要有数学赋于的权利,也要有现实的合理性,还要符合数学内部的和谐一致.1.2 用数学的思维分析世界
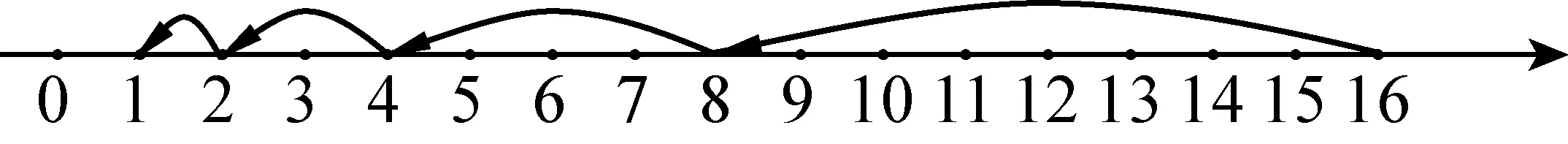
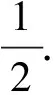
1.3 用数学的语言表达世界
2 几点思考



