设计有价值的问题 促进学生自主建构——以“两角和与差的余弦”为例

许兴震

(江苏省邗江区教育局教研室225009)

1 问题提出

体验、揭示知识发生、发展和形成的过程，帮助学生自主建构认知体系，促进学生思维能力的发展，是数学概念(公式)教学的核心任务.为了在实践中落实上述要求，笔者开展了“问题引领，自主建构”数学教学模式的研究，主要做法就是教师通过重构教材内容，通过设计有价值的问题(串)，引领学生开展深度思维，突破自主建构的瓶颈，学生在感受问题、提出问题、探究问题和解决问题的过程中，萌发学习动机和欲望，形成积极的学习态度，成为信息加工的主体和知识意义的建构者，并在此过程中获得个人的全面发展.下面，笔者以近期参加市高中数学骨干教师课堂教学能力考核的课例苏教版必修4第三章“三角恒等变换”第一课时“两角和与差的余弦”为例，谈谈通过设计有价值的问题，促进学生自主建构的一些做法，请读者批评指正.

2 教学案例

2.1 创设情境，提出问题

苏教版高中数学实验教材关于教学内容的呈现，高度重视问题情境的创设，但是教材中情境的创设往往是粗线条的，有些还是跳跃性的.学生对学习新知识的必要性，教材为何要按照这种顺序安排学习内容，用什么方法来研究新的知识，难以理解到位，对学生自主建构知识意义产生消极影响.因此，教师要按照教材的编写思路、知识的逻辑顺序和学生的认知规律，通过设计问题串，对教材创设的问题情境进行重构，使学生在问题情境中产生认知冲突，发现和提出问题，从而激发学生积极思维的动机和探索问题的欲望.

问题1前面，我们学习了任意角的三角函数和诱导公式，知道了同角三角函数之间的关系，可以用正弦、余弦、正切函数中的一个表示其余两个，那么，两个角的和与差的三角函数与这两个角的三角函数有什么关系？今天这节课，我们就来研究两角和与差的余弦.

问题2如何研究？教材在今天研究三角函数与上次研究三角函数之间安排了第2章平面向量，这说明什么呢？

问题3平面向量中的哪个知识点与三角函数有联系呢？向量的数量积的定义和坐标表示分别是什么？

生：a·b=abcosθ，θ是向量a、b的夹角，θ∈0,π；设a=(x1,y1)，b=(x2,y2)，a·b=x1x2+y1y2.

问题4设a=(cosx,sinx)，b=(1,1)，请用上面两种方法分别计算a·b.你能得出什么结论?

问题5cos(α-β)能否用α的三角函数与β的三角函数来表示？

意图教材中的情境设计是由求两个向量的数量积引入的，并未直接回答学习新知识的必要性，也未解释为何要把向量的数量积作为新知识的“生长点”，教师要分析学生在自主建构过程中可能出现的难点并将其梳理出来，通过设计针对性的问题，揭示出知识“发生”的背景和生成新知识的“生长点”，也为学生开展探究活动提供了研究的方向和研究方法.

2．2 意义建构，解决问题

学生对知识意义的建构，与问题发现、探究与解决相随相伴，同步推进.因此，在提出核心问题以后，教师要在学生的“最近发展区”上设计问题(串)，引导学生自主探究，让学生的思维逐步逼近问题的“核心地带”，自主的开展知识的建构.

探究1公式的“发现”

问题6为什么会出现这个问题？有什么办法解决这个问题？

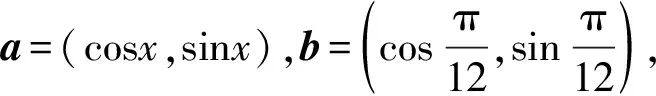
问题8这个公式能否推广到一般情形吗？

生：α、β为任意角时，cos(α-β)=cosαcosβ+sinαsinβ. (C(α-β))

探究2公式的证明

有了问题4、问题7的铺垫，用“算两次”的办法，学生很快得出了下面的结论.

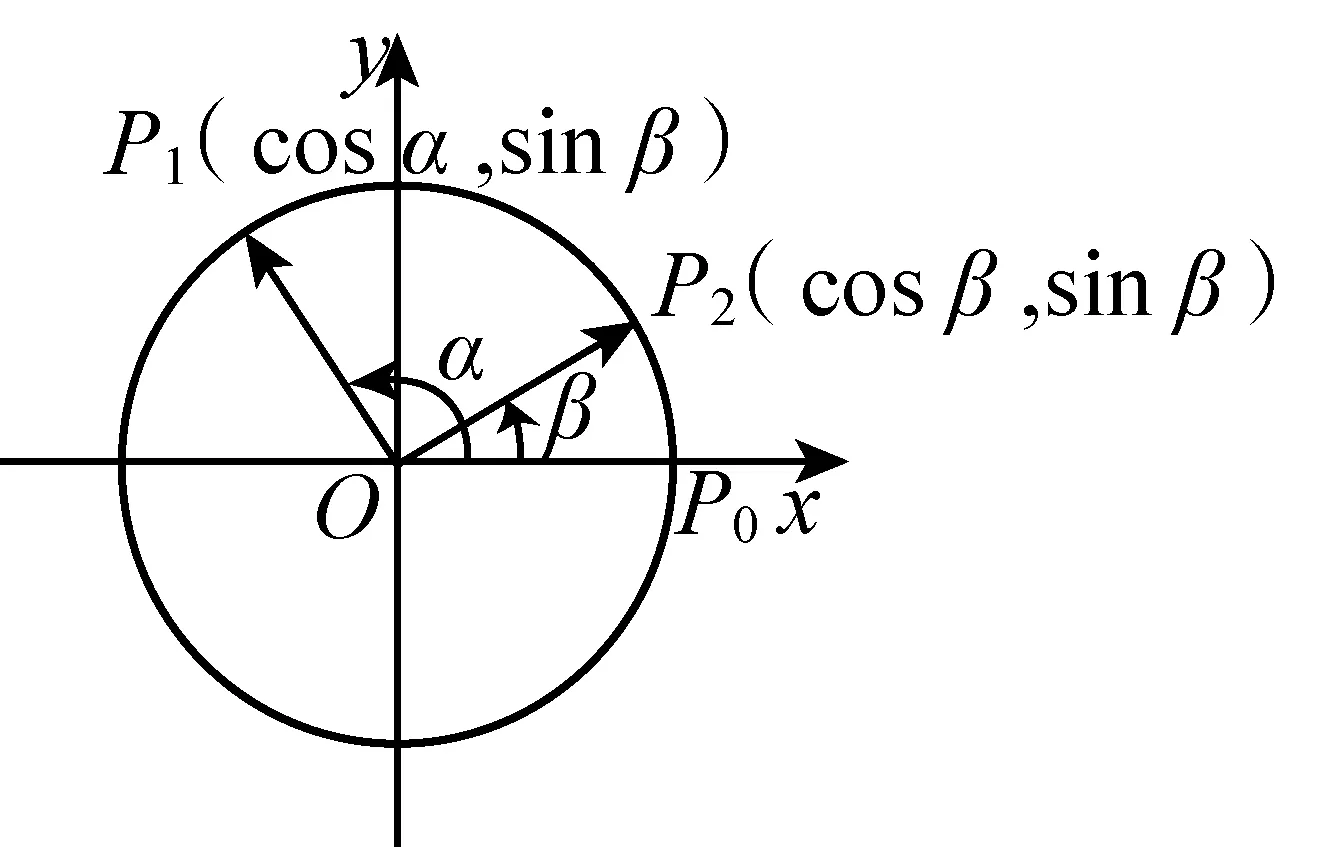
另一方面，由向量数量积的坐标表示，有a·b=cosαcosβ+sinαsinβ，所以，cos(α-β)=cosαcosβ+sinαsinβ.

问题9上面的证明有什么问题？

生：上述证明过程中，α-β不一定是向量a、b的夹角.但是，我觉得难以说清楚.

师：遇到比较抽象的问题，我们常用的思路是什么？请同学们任取一组α,β看一看，并求出两个向量的夹角θ.

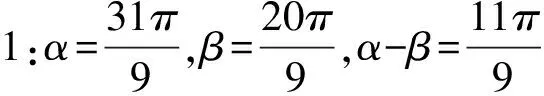
师：从中能发现什么规律？分组讨论.

生3：当α-β∉0,2π时，由于余弦函数的周期为2π，所以，我们可以首先利用诱导公式，把α-β转化到0,2π；当α-β的终边落在0,π时，θ=α-β；当α-β的终边落在(π,2π)，由于余弦函数是偶函数，一定可以在0,π内，找到一个角θ=2π-(α-β)，使得cos(α-β)=cosθ，因此，我们只需考虑0≤α-β<π的情况，从而α-β就是向量a、b的夹角θ.

意图当α，β为任意角时，向量a、b的夹角θ的确定是本节课的一个教学难点，也是影响学生自主建构的瓶颈.虽然教材上作了说明，由于比较抽象，学生难以理解.如何突破瓶颈？教师没有直接给出答案，由于学生具备了诱导公式的基础，因此教师从学生的立场出发，遵循学生的认知规律，让学生从特殊值开始探究，自主探寻出蕴含着的一般规律：将任意角→0,2π→0,π，cos(α-β)=cosθ均成立.这个过程，给教材上的有关说明作了一个很好的诠释，将知识从学术形态转变为教育形态.

生：α=θ+β+2kπ或β=θ+α+2kπ(k∈Z)，即θ=α-β-2kπ或θ=β-α-2kπ(k∈Z)，等式cos(α-β)=cosθ总是成立.

意图问题9的探究，师生对向量a、b的夹角的讨论，从特殊值开始，探寻一般性的处理方法；问题10的设计就是引导学生探究公式严格的证明，回避了对向量a、b的夹角的讨论，利用数形结合的数学思想方法，简洁、严谨地给出了证明.

探究3其他证法的探究

问题11有没有其他证法了？

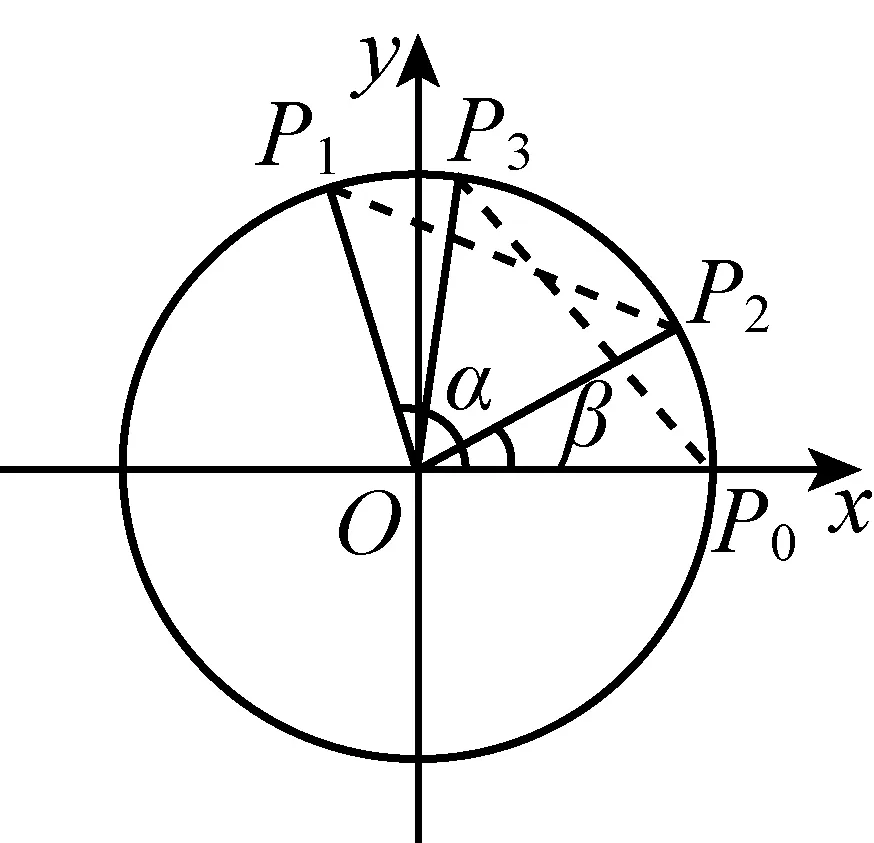
师：在这个公式中，涉及到α、β、α-β三个角，在直角坐标系中xOy中，以x轴为始边，分别作出这三个角.为了研究问题的方便，我们不妨假设：α∈0,π，β∈0,π，α>β，分别作出α，β，α-β的终边，分别与单位圆交于P1,P2,P3，单位圆与Ox轴交于P0.

问题12请大家观察，在单位圆中你能得到什么结论？

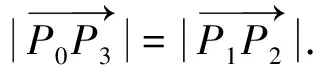
生：P0(1,0)，P1(cosα,sinα)，P2(cosβ,sinβ)，P3(cos(α-β),sin(α-β)).

问题13请大家用坐标表示，并进行化简，能得到什么结论？

生：cos(α-β)=cosαcosβ+sinαsinβ.

问题14α=β或α<β，等式还成立吗？

学生验证，公式对α=β或α<β均成立.这说明，公式对于α,β∈0,π均成立.

问题15大家讨论一下，怎样将α,β的范围推广到R？

通过讨论，大家拿出了推广方案.

问题16当α,β∈π,2π时，结论成立吗？

通过讨论，学生联想到问题9中对两个向量的夹角的处理方法，很快解决了问题.

2π-α∈0,π，2π-β∈0,π，从而满足上述结论，

cos(2π-α)+(2π-β)=cosαcosβ+sinαsinβ，

cos(α-β)=cosαcosβ+sinαsinβ(α,β∈R).

问题17其他情形，我们又如何证明呢？

生：利用诱导公式即可证明.

意图问题11是教材中的探究内容，证明过程需要对角α,β的范围进行分类讨论，因而对学生思维能力的要求较高，是本节课学生自主建构的另一难点.教师通过设计一组有易到难、层层递进的问题串，采取了化整为零、化生为熟策略，引领学生突破自主建构的瓶颈.其思路是α,β从0,π→0,2π→任意角，公式C(α-β)均成立，这种方法实际上是前一个证明方法的一种迁移.

问题18如何得到两角和的余弦公式？

生：用cosα+β=cosα--β

=cosαcos-β+sinαsin-β

=cosαcosβ-sinαsinβ.

师：两角和的余弦公式

cosα+β=cosαcosβ-sinαsinβα,β∈R.

2.3 拓展应用，反馈矫正

例1利用两角和(差)的余弦公式证明下列诱导公式：

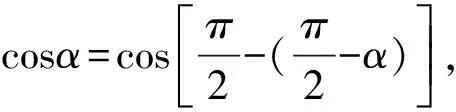
例2利用两角(差)的余弦公式，求cos75°，cos15°，sin15°，tan15°.

意图进一步熟练使用两角和与差的余弦公式、例1中的诱导公式，渗透化生为熟的化归思想.

意图熟悉公式的运用,对照公式,分清已知和未知,运用同角三角函数之间的关系求三角函数值时,应根据角的范围，正确确定两角正、余弦值的范围.

3 设计有价值的问题，促进学生自主建构教学的几点思考

问题是数学的心脏，是科学探索的出发点和动力.新课改倡导以问题为中心的教学，引导学生以高水平的思维活动开展学习，通过问题解决来自主建构知识.实践证明：不同的问题所引起的学生思维参与程度是不一样的，其对于学生理解和掌握知识的作用也不相同.教师要通过设计有价值的问题，引导学生在积极思维过程中，自主建构知识意义.关于有价值的问题，不少学者从不同角度开展了研究，为我们开展深入开展课程改革提供了指导和方向.笔者认为，有价值的问题应该包括下列特征.

3.1 围绕目标，突出教学重点和难点

教学目标对课堂教学活动起着指导作用.有价值的数学问题，首先应该服从于教学目标的达成，只有这样才能保证教学活动的开展和学生对知识意义的自主建构沿着正确的方向展开.教学重点和教学难点是师生活动的密集之处，如何突出重点、突破难点是教师在设计教学活动时思考的主要内容，教师需要设计出有价值的问题，并发挥其桥梁作用，引领学生与教材进行沟通，引导学生开展更有效、更深入的探究活动，促进学生对知识意义的自主建构.实践证明，问题对教学目标、教学重点和难点指向性越明确，越能激发起学生的求知欲望，建构活动就能沿着正确的方向推进，教学目标的达成度就越高.

3.2 关注学情，彰显主体地位

将教学内容进行问题化设计，问题就成为引领学生探究的载体，学生的学习活动就转化为学生的探究活动.学生是探究活动的主体，因此学生的认知基础、学习能力等学情状况就成为影响教师设计有价值问题的关键因素.对于学生来说，问题过易，无需探究，建构不了新知；问题过难，探究无法展开，自主建构难以推进.因此，有价值的问题一定要找准学生的认知起点，与学生的学习能力相适切，位于学生的“最近发展区”之内，才能实现真正的对知识意义的自主建构.

3.3 启发性强，提供迁移空间

课堂教学中，教师不仅要指导学生解决问题，更重要任务是通过对分析、思考，抽象出蕴含其中的一般性的思想方法，进而推广到更一般的情形和其他特殊的情形中，促进学生能力的提升.因此，有价值的问题，其解决的方法要有一定的启发性，学生通过思考、探究等手段能够得出多种解决的路径，其解决的方法可以迁移到解决类似的问题过程中.

3.4 具有层次性，引领思维逐步深入

学生是问题探究的主体，其抽象逻辑思维能力正处于发展阶段，认识事物的过程必然是渐进式的，而非跃进式的.因此，有价值的问题(串)要符合学生的思维发展规律，体现层次性.对于难度较大的问题，可以设计具有一定的逻辑联系、有一定层次的问题，以问题串的形式，引领学生进行系列的、连续的思维活动，使学生的思维逐步攀升到新的高度.这样的问题(串)，能循序渐进地引导学生思维的发展，逐步加深对问题本质的认识，促进学生对知识意义的自主建构.

3.5 引发合作探究，体验建构过程

问题是教师引领学生探究的平台，学生对知识意义的建构，与问题的探究和解决相随相伴，没有探究，真正的自主建构就不会发生.因此，有价值的问题，会能够引发学生的探究活动，让学生体验知识意义的建构过程.教材中知识的呈现形态更多是学术形态，教师的重要任务就是通过将教学内容设计成有价值的问题，引发合作探究，通过尝试、操作、想象、归纳、抽象等思维参与，实现对知识意义的“再创造”和“再发现”，进而将知识的学术形态转化为教育形态，而不是将书本知识灌输给学生.