一个三角等式证明及其应用

杨学枝

(福建省福州第二十四中学 350015)

本文首先给出一个常见的三角等式，并用多种方法证明，然后举例说明其应用.

定理设α,β,γ是任意实数，则

cos2α+cos2β+cos2(α+β)-2cosαcosβcos(α+β)=1，

或

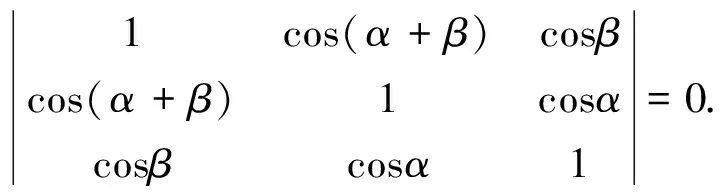
下面我们给出定理中的等式的十种证法，这十种证法各有特色，富有启发性.

证一应用和差化积及半角公式.

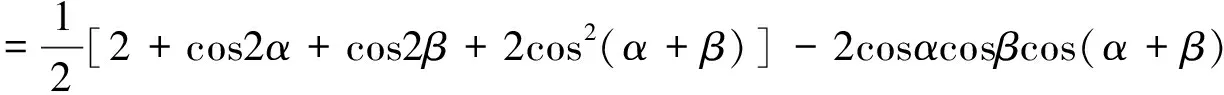
=1+cos(α+β)[cos(α+β)+cos(α-β)]-2cosαcosβcos(α+β)

=1+2cosαcosβcos(α+β)-2cosαcosβcos(α+β)=1=右边，

故定理获证.

证二应用积化和差及倍角公式.

左边=cos2α+cos2β+cos2(α+β)-cos(α+β)[cos(α+β)+cos(α-β)]

=1=右边，

故定理获证.

证三应用两角和的公式和诱导公式.

左边=cos2(α+β)+cosα[cosα-cosβcos(α+β)]+cosβ[cosβ-cosαcos(α+β)]

=cos2(α+β)+cosα[cos(α+β-β)-cosβcos(α+β)]+cosβ[cos(α+β-α)-cosαcos(α+β)]

=cos2(α+β)+sin(α+β)cosαsinβ+sin(α+β)sinαcosβ

=cos2(α+β)+sin(α+β)(sinαcosβ+cosαsinβ)

=cos2(α+β)+sin2(α+β)=1=右边，

故定理获证.

证四应用两角和的公式和诱导公式.

由于cos(α+β)=cosαcosβ-sinαsinβ，即有

sinαsinβ=-cos(α+β)+cosαcosβ，

将上式两边平方得到

sin2αsin2β=cos2(α+β)+cos2αcos2β-2cosαcosβcos(α+β)，

又由于sin2α=1-cos2α，sin2β=1-cos2β，代入上式，并经整理即得定理中的等式.

证五应用sin(α+β)=sinαcosβ+cosαsinβ，证法同上面证四(从略).

证六先配方，再应用两角和的公式及诱导公式.

左边=[cos(α+β)-cosαcosβ]2+cos2α+cos2β-cos2αcos2β

=(sinαsinβ)2+cos2α+cos2β-(1-sin2α)(1-sin2β)

=cos2α+cos2β+sin2α+sin2β-1=2-1

=1=右边，

故定理获证.

证七当sinα,sinβ,sin(α+β)有一个为零时，不妨设sinα=0，则α=kπ(k∈Z)，这时有

原式左边=cos2α+cos2β+cos2(α+β)-2cosαcosβcos(α+β)

=1+cos2β+cos2(kπ+β)-2coskπcosβcos(kπ+β)

=1+cos2β+cos2β-2cos2β=1=右边，

原式成立.

当sinαsinβsin(α+β)≠0时，可利用代数恒等式及余弦定理证明定理中的等式成立.

利用恒等式(证明从略)

x(-x+y+z)2+y(x-y+z)2+

z(x+y-z)2+(-x+y+z)(x-y+z)·

(x+y-z)=4xyz.

若在上式中取x=sin2α,y=sin2β,z=sin2(α+β)，xyz≠0，并注意到等式(证明从略)

-sin2α+sin2β+sin2(α+β)=2sinβsin(α+β)cosα，

sin2α-sin2β+sin2(α+β)=2sinαsin(α+β)cosβ，

sin2α+sin2β-sin2(α+β)=-2sinαsinβcos(α+β)，

即得到定理中的等式.

证八应用两角和的公式和行列式运算.

当sinαsinβsin(α+β)=0时，原式成立，可见上面证七.

当sinαsinβsin(α+β)≠0时，由于

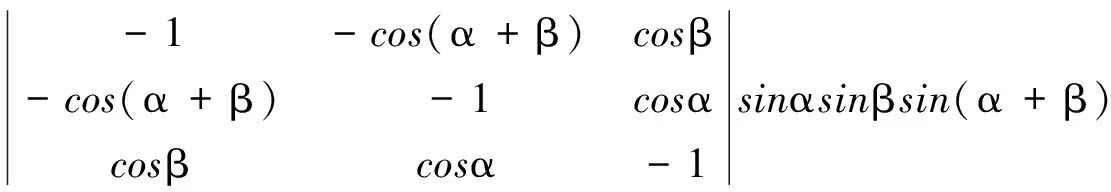
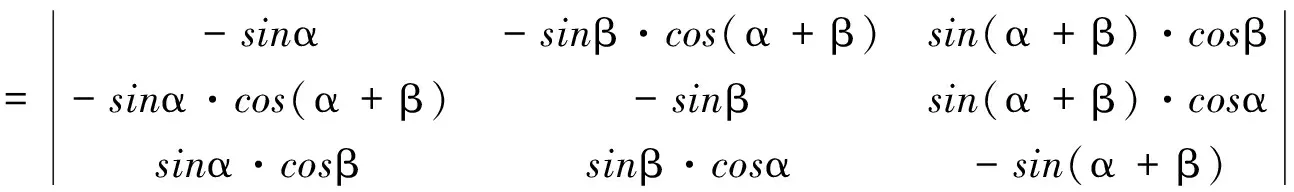
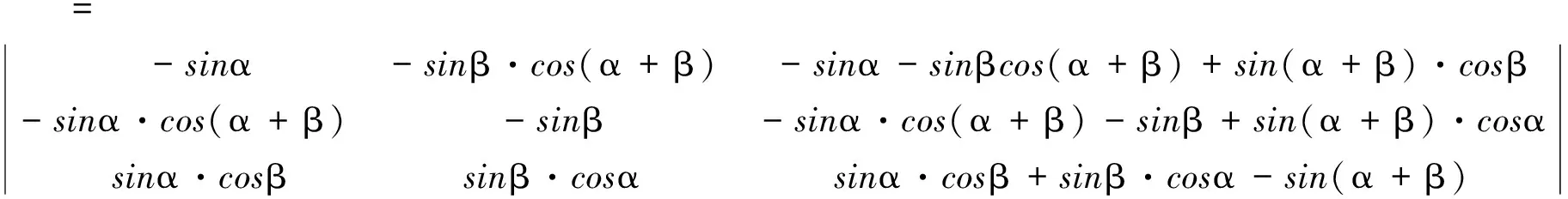
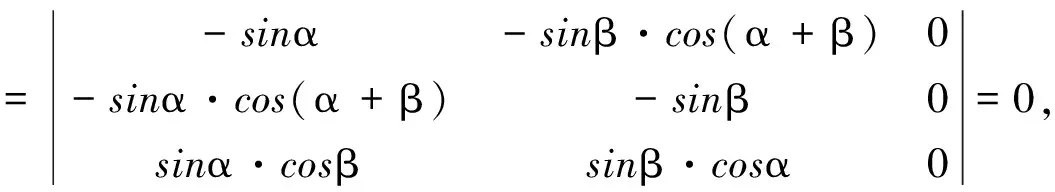
故有

展开即得定理中的等式.

证九应用两角和的公式以及方程性质.

由两角和公式，有

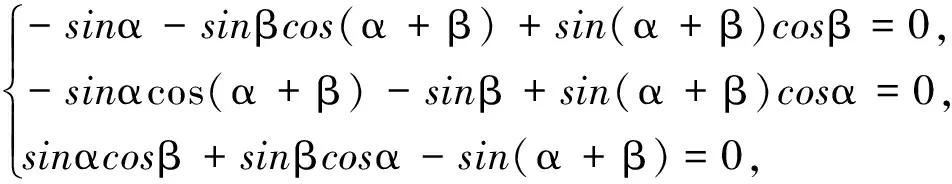
设x=sinα,y=sinβ,z=sin(α+β)，则以上方程组即为

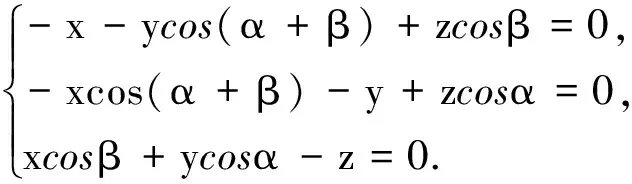
若xyz=0，上面证七中已经证明，这时原式成立.

若xyz≠0，由于上述方程组对于x,y,z是齐次线性方程组，有非零解，因此有

展开即得定理中等式.

证十设平面上一点O，射线OA，OB，OC的长度均为1，OB与OC成角为α，OC与OA成角为β，则OA与OB成角为-(α+β).由于平面上任意三个非零实数向量都线性相关，即总存在不全为零的两个实数λ,u，满足

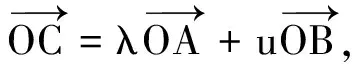
于是有

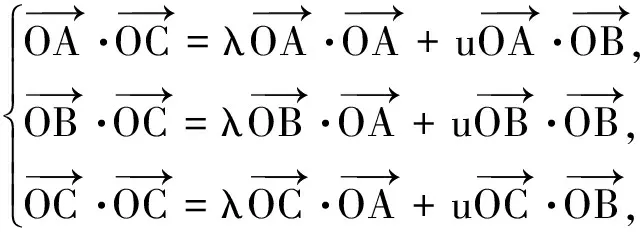
即

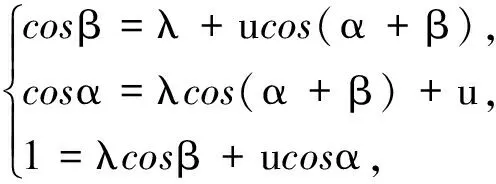
由以上关于λ,u的线性方程组，消去λ,u，便得到行列式

即

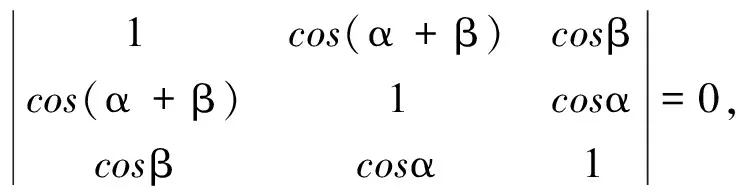
展开即得定理中等式.

由定理1即可得到以下推论.

推论1设A,B,C是任意实数，且A+B+C=(2k+1)π(k∈Z)则

cos2A+cos2B+cos2C+2cosAcosBcosC=1.

或写成下列行列式：

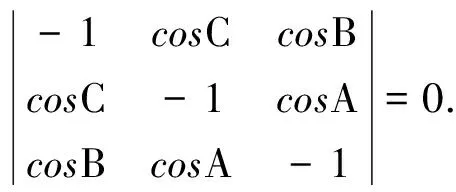
推论2设α,β,γ是任意实数，且α+β+γ=2kπ(k∈Z)则

cos2α+cos2β+cos2γ-2cosαcosβcosγ=1.

或写成下列行列式：

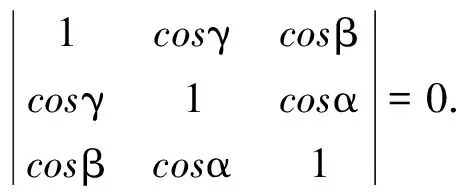
由推论1中的等式可得到

2cosAcosBcosC=sin2A+sin2B+sin2C-2，

再将上式两边平方，并应用cos2A=1-sin2A等，经整理，可得到以下

推论3设A,B,C是任意实数，且A+B+C=kπ(k∈Z)则

4sin2Asin2Bsin2C

=2∑sin2Bsin2C-∑sin4A.

推论3也可以用三角形面积海伦公式推导得到，由于

16Δ2=2∑b2c2-∑a4

=4R4(2∑sin2Bsin2C-∑sin4A)，

Δ=2R2sinAsinBsinC，

由上面两个三角形面积公式，即可得到推论3中的等式.

推广设α,β,γ∈R,则

cos2α+cos2β+cos2γ+cos2(α+β+γ)

=2[1+cosαcosβcosγcos(α+β+γ)+

sinαsinβsinγsin(α+β+γ)].

由等式cos(α+β)=cos[(α+β+γ)-γ]得到

cosαcosβ-cosγcos(α+β+γ)

=sinαsinβ+sinγsin(α+β+γ),

将上式两边平方,并应用等式

sin2α=1-cos2α,sin2β=1-cos2β,

sin2(α+β+γ)=1-cos2(α+β+γ),

即可得到.

上述定理及其推论有着广泛的应用.下面略举几例.

例1设α,β∈(0,π)，满足

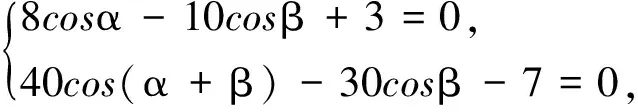
求cosα，cosβ的值.

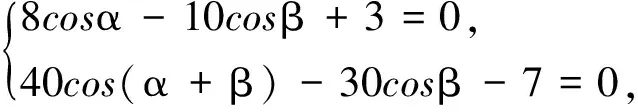
得到

代入定理中的恒等式

cos2α+cos2β+cos2(α+β)-2cosαcosβcos(α+β)=1，

并经整理得到

1500cos3β-2600cos2β+435cosβ+663=0，

即

(15cosβ-17)(100cos2β-60cosβ-39)=0，

由于15cosβ-17≠0，因此

100cos2β-60cosβ-39=0，

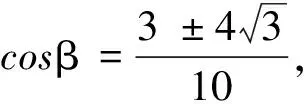
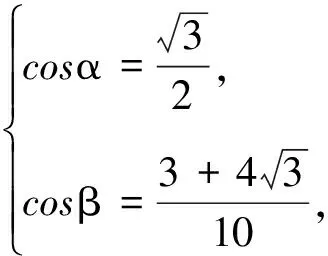
例2△ABC为逆时针转向，其三个内角为A,B,C，若P点为△ABC所在平面上一点，已知PA=R1,PB=R2，PC=R3，求△ABC三边长.

解i)当P点为外接圆内或外接圆上一点时.

设△ABC外接圆半径为R，则三边长为BC=a=2RsinA，CA=b=2RsinB，AB=c=2RsinC，射线PB到PC，PC到PA，PA到PB的角(均为逆时针方向)分别为α,β,γ，则有α+β+γ=2kπ(k∈Z).于是，由余弦定理得到

再利用三角函数恒等式(前面已证明)：若α+β+γ=2kπ(k∈Z)，则有

cos2α+cos2β+cos2γ-2cosαcosβcosγ=1，

将上面三式代入，便有

即

整理得到

(※)

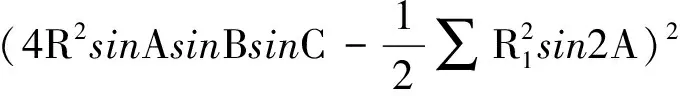
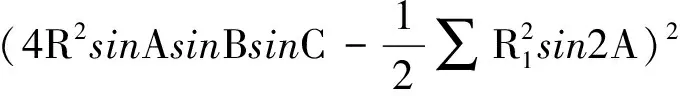
sin2C)

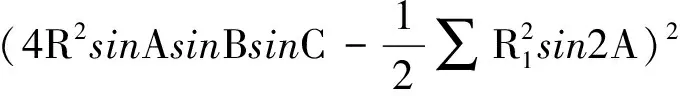
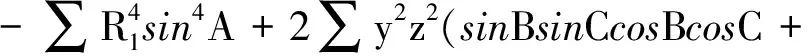
sinBsinCcosA)

(※※)

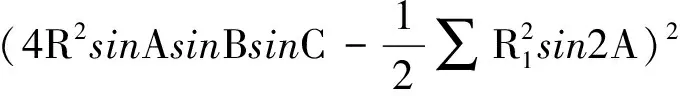
下面说明，当P点为△ABC外接圆内或外接圆上一点时，有

由于△ABC为逆时针转向，△ABC面积为正.从P点分别向三边BC,CA,AB引垂线,垂足分别为A′,B′,C′ 记△ABC与△A′B′C′的有向面积分别为Δ与Δ′，△A′B′C′三边长分别为B′C′=a′,C′A′=b′,A′B′=c′,并注意到

Δ=2R2sinAsinBsinC，

=Δ′，

可知, 若P点为△ABC外接圆内或外接圆上一点时，△A′B′C′面积Δ′≥0，因此有

=2Δ-2(Δ-2Δ′)=4Δ′≥0,

当且仅当P在△ABC外接圆上时Δ′=0[1].

因此，由式(※※)可求得

由此得到

于是，便可求得△ABC三边

ii)当P点为△ABC外接圆外一点时，Δ′<0，因此有

因此，有

由式(※※)，可以得到以下等式：

以上Δ,Δ′为有向面积.

例3半径分别为a,b,c的三个圆E，圆F，圆G，两两相外切，求同时与上述三个圆均外切的小圆的半径r.

解答见文[2].

例4若四面体ABCD，由顶点D出发的三条棱长为DA=a,DB=b,DC=c，底面ABC的面积为Δ，记∠BDC=α，∠CDA=β，∠ADB=γ，四面体ABCD体积为V，则有

证明设BC=a′,CA=b′,AB=c′，从D作DH⊥平面ABC，垂足为H，设HA=R1,HB=R2,HC=R3，射线HB到射线HC，射线HC到射线HA，射线HA到射线HB的角分别为α′,β′,γ′，则α′+β′+γ′=2kπ(k∈Z)， 且有

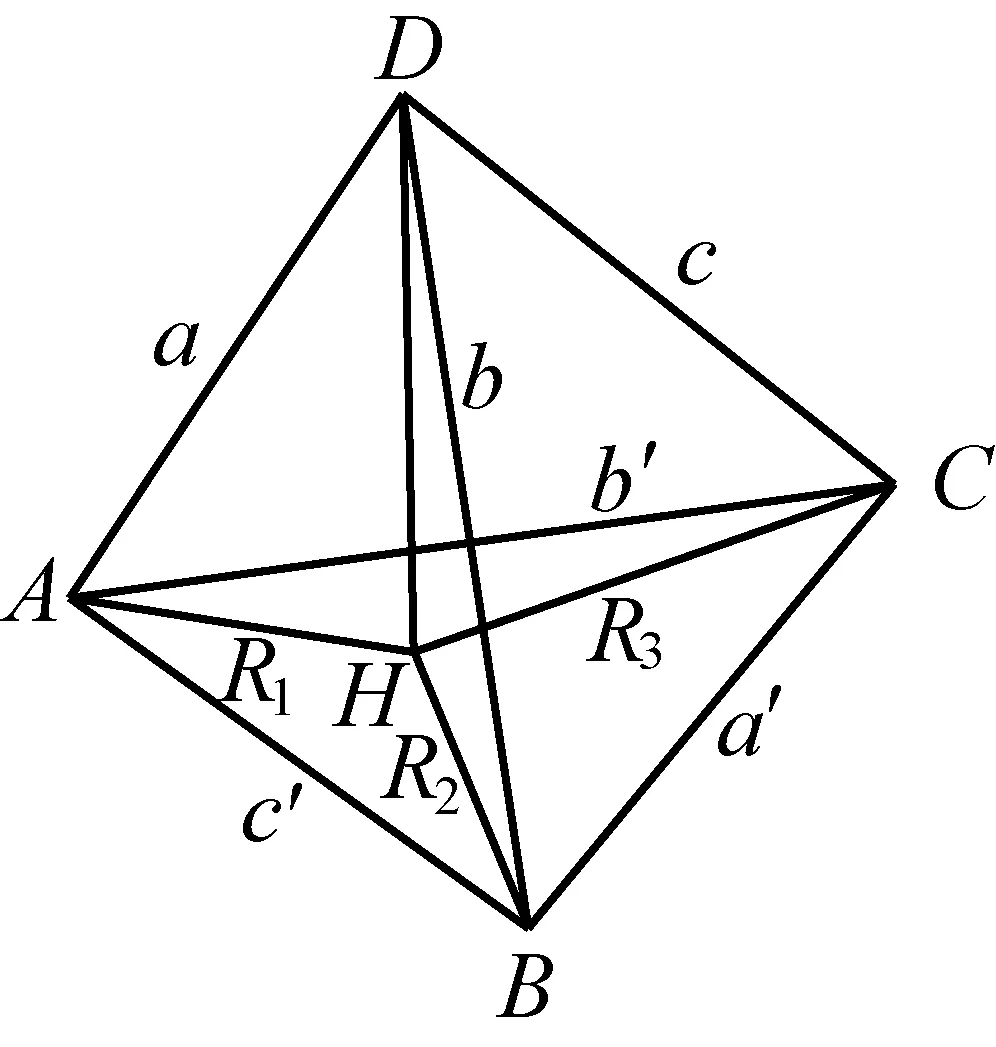
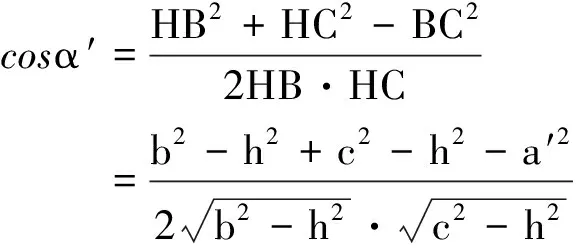
同理，有

代入等式

cos2α′+cos2β′+cos2γ′-2cosα′cosβ′cosγ′

=1，

(据推论2)得到

=1，

上式经化简，得到

16Δ2h2+a2(b2+c2-a′2)2+

b2(c2+a2-b′2)2+c2(a2+b2-c′2)2

-(b2+c2-a′2)(c2+a2-b′2)(a2+b2-c′2)

-4a2b2c2=0，

由此，可以求得

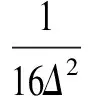
b2(c2+a2-b′2)2-c2(a2+b2-c′2)2

+(b2+c2-a′2)(c2+a2-b′2)(a2+b2-c′2)

+4a2b2c2]

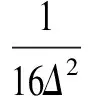
-4a2b2c2cos2γ

+8a2b2c2cosαcosβcosγ+4a2b2c2)，

+2cosαcosβcosγ)，

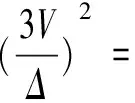
由此便得到

许多数学参考书中对于例4中的四面体体积公式的证明都比较麻烦，这里我们给出了一个初等的证明.

本文定理还有许多应用，限于篇幅就不累赘了.