三线相融：指向学生的深度发展

【摘要】《义务教育课程标准（2011年版）》指出：有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学生学习数学的重要方式。然而在小学数学教学中，学生还未能充分经历探究和思考的过程。因此，对教材，对教法，对学生进行深度研究，指向的是学生的数学发展。具体方法有：解读文本之线，打通教材编写的脉络;寻求教者之线，推敲适合学生的教法;基于学生之线，循着思维的发展前行。

【关键词】解读文本 寻求教法 基于学生 三线相融

《义务教育课程标准（2011年版）》指出：学生的数学学习内容应当是现实的、有意义的、富有挑战性的，这些内容要有利于学生主动地进行观察、实验、验证、推理与交流等教学活动。有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学生学习数学的重要方式。

基于这一理念，在数学教学中，我们有必要让学生经历或部分经历数学知识发生、发展的过程，不管是类似于揭示“规定”的教学，还是后续内容提前来教，都应该让学生经历深刻的学习体验，感受其数学本质，使之在学习冲突中不断地向数学“规律”迈进，从多样复杂的现象中看清其本质，感受到数学的简单，并在探索的过程中培养学生严谨、理性的学习态度。

那么，如何使学生获得深刻的学习体验呢？

一、解读文本之线，打通教材编写的脉络

教材的文本内容都是静态的，浓缩的，作为教师应从不同的角度细细研读教材，深入挖掘教材内在联系，进行个性化的解读。

1.理解教材编写结构，展示知识形成过程

数学教材具有较强的系统性和逻辑性，各部分内容之间的联系十分紧密。教师需认真钻研教材，既要熟悉本课内容，又要熟悉本册内容，还要熟悉相邻年级的内容，甚至要熟悉整个小学阶段的内容，整体把握各部分内容，理解知识之间的联系及教材编排意图。

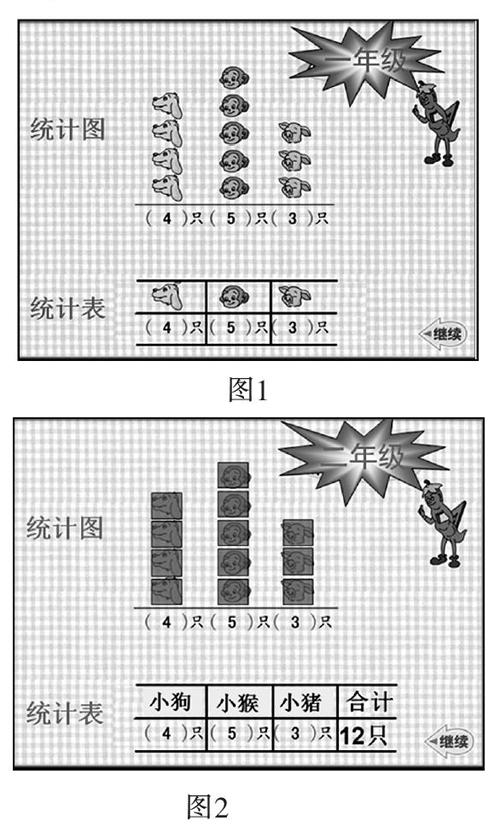
如，教学五年级上册《复式统计图》。

师：一年级的时候，我们就会从情境图中找动物，并且把这些动物分类排成一排，然后我们可以把各个小动物的个数统计在这样的表中（如图1），这就是我们最初学习的统计图和统计表（板书：统计）。到了二年级，统计表中的小动物变成了动物的名称，添了“合计”栏，而统计图中的小动物变成了一个个小方块（如图2）。把这些小方块垒起来，旁边标上数值，这就变成了三年级学习的条形统计图（如图3），再把条形统计图的直条变一变，压缩一下，把最顶上的点连成线（如图4），这就是折线统计图，四年级学习的内容。四年时间，我们学了很多统计知识了，统计图变了好多了，那咱五年级又准备变什么呢？

教学本课时，正是利用了教材间的联系，在原有基础上变一变，使学生获得新知。为很好地展示数学知识形成的过程，教师在教学前，认真阅读教材内容，充分理解教材的编写意图，发掘教材之间的联系，把已经学过的一至四年级的统计知识理一理，变一变，串成一条线，使学生清楚地理解知识之间的变化，对学习下一部分内容产生浓厚的兴趣。

2.对比不同版本教材，沟通知识呈现方式

教师能否整体把握教材，不但体现在能否纵向把握知识脉络上，还体现在能否横向沟通知识联系上。教师要通过新旧教材的对比、不同版本的对比等方式，科学解读教材的变化。

如，解读新旧教材的变化：五年级下册《简易方程》中的“解方程”，原先的教材是根据四则运算各部分之间的关系变形求解的，新教材的解方程的变形依据是天平保持平衡的原理，即等式的性质。为什么进行这样的改动呢？通过对比初中教材和小学教材，发现了改编的原因：原先小学教学简易方程，其实是用算术的思路求解，到了中学又要另起炉灶，重新学习等式的性质解方程。

又如，不同版本教材的变化：人教版四年级下册《小数的意义和性质》整个单元分小数的意义和读写法、小数的性质和大小比较、小数点移动引起小数大小的变化、小数与单位换算以及小数的近似数几个部分，与苏教版不同的是加了小数与单位换算这节内容（如图5和图6）。

而苏教版教材从三年级下册开始，以“长度单位”为例认识了一位小数后，接着编排了例题“1元2角，3元5角可以写成多少元”，并在习题中安排了单位改写（如图7）。在五年级上册安排了试一试（如图8），苏教版教材虽然并没有用专门的章节来教学单位换算，但是却分散在不同的单元，以习题、试一试等形式穿插进去。如果教师能经常阅读并对比不同版本的教材，那么，处理这些习题和试一试的时候，完全可以借鉴人教版的方法。

二、寻求教者之线，推敲适合学生的教法

“一千个读者就有一千个哈姆雷特。”同一课的内容，不同的教师就会有不同的解读。教师在深入理解教材的基础上，还要针对不同班级的学生情况，找寻适合学生的教學方法。

以三年级上册“两位数除以一位数”一课为例，不同的教师就有不同的教学：

【教师A】理解算理，形成算法。

师：46÷2=？你想怎么算？

生1：每班先分得2筒，是20个，再分得3个，合起来是23。

师：让我们一起来把分小棒的过程说一说：先把（  ）平均分成2份，每份（  ），再把（  ）平均分成2份，每份（  ），最后，把（  ）和（  ）合起来，就是（  ）。（如图9）

师：46÷2=？可以用竖式计算。请你试一试。

师：你们觉得哪种写法更能清楚地表示出分两次的过程？（如图10）

师：我们在分小棒的过程中，是分两次来分小棒的，为了体现这个过程，数学中规定，我们写竖式的时候也要分两步来写。（如图11）

教师A教学中结合分小棒的过程使学生认识到两位数除以一位数，要分两步除，然后通过对比学生的竖式，强调竖式书写也要分两步。

【教师B】他山之石，可以攻玉。

师：16个羽毛球平均分给2个班，每班分得多少个？

生：把一捆小棒拆开来，和6根合起来是16根，平均分成2份，每份8根。（如图12）

师：46个羽毛球平均分给2个班，每班分得多少个？

生：先分4捆，再分6根，最后把他们合起来。

教师板书竖式，强调分两次。（如图13）

师：56个羽毛球平均分给2个班，每班分得多少个？你准备分几次？

生：先把4捆小棒分成2份，每份两捆，再把剩下的1捆拆开来跟剩下的6根一起分成2份，每份8根。（如图14）

师：56÷2=？也是分两次除，竖式分“两层楼”写，那么再回过去想想，46÷2=？的竖式怎么写比较好？（如图15）

师：同学们写出了两种不同的竖式，那么，哪种写法更合理、更规范呢？我们先放一放，我们一起来研究一下，56÷2=？该怎么除？竖式又是如何写呢？

为了避免学生出现图10左边的写法，教师B调整教学过程，先复习以前学过的表内除法，再把首位能整除的和后一堂课“首位不能整除”的内容都放在一堂课中教学，这种以“他山之石，可以攻玉”的方法，让学生通过对比，发现“两层楼”书写竖式的必要性。

数学教学中会遇到很多“数学规定”，针对这些 “规定”，教师通常采用直接告知或让学生阅读课本的方式进行教学，并以“规定”为理由而让学生强行识记。久而久之，在学生的心中就会积压着越来越多的“为什么”，他们会觉得数学教师“不讲理”。其实，这些“规定”背后，也有着其合理性缘由，只要我们认真思考，就能发现其更为丰富的内涵。我们在教学时，也应尽可能地创造条件，让学生经历或部分经历“规定”从无到有的形成的过程，揭示“数学规定”背后的奥秘，让学生领悟“数学规定”。

三、基于学生之线，循着思维的发展前行

学生是课堂的主人，课堂教学的一切皆应为学生服务。他们有太多的“为什么”，且有弄清这些“为什么”的强烈需求。我们的数学课堂须站在“学生立场”，要主动弄清学生在课堂中的所思、所想、所惑，并保护他们这种与生俱来的需求。课堂上，我们要顺应思维发展的轨迹，带领他们探索，经历完整的探究过程，并在他们的疑惑处进行适时启发和点拨，启发他们进行分析与推理。

1.基于学生视角探寻“原点”

学生作为独立个体，在生活学习中积累了一定的经验基础，学生学习成长的过程就是在已有知识基础这个“原点”上逐渐提升的过程，脱离了“原点”，一切学习活动都是徒劳。作为教师应该从学生视角分析学习者“现有水平”和“可能发展水平”之间的差距，并以此来设计、展开教学活动。

如，教学五年级上册《小数的意义》。

师：生活中，很多地方都能见到小数。瞧！赛跑的成绩，我们的身高、体重、体温等。在进行测量和计算时，往往不能正好得到整数的结果，根据需要便产生了小数。一起来回顾一下，你能说说1分米等于几分之几米？写成小数是多少米？3分米呢？

师：你能用你喜欢的方式表示出0.5米吗？桌子上有一些材料你们可以自己选用。（如图16）

师：课桌的高比5分米多2厘米，也就是52厘米，52厘米是多少米呢？你能继续分吗？（如图17）

对一节课的学习，学生的认知“原点”非常重要。在已有知识经验的基础上教学，学习过程自然流淌，虽有波澜或坎坷，但学习者能主动而勇敢地学习，保持强烈的学习欲望，真正具有生命力。

2.立于学生立场打造“圆点”

基于学生立场的课堂，注重学生自主学习、独立思考、实践操作，学生的学习是真实发生的，是看得见，摸得着的，能让教师感受到的。他们眼睛受智慧启迪发亮，凝神静思，神情专注，一只只手臂高高举起;他们有兴趣，喜欢做，主动获取，积极操作，合理应用。

（1）真实操作，增加学生活动经历

课堂上，学习是真正发生的，不是学生在学习上顺着教师的思路顺利完成学习任务，而是学生真正参与到课堂中，动手操作，自主探究，不断尝试，在一次次地操作中积累数学活动经验。

例如，教学《表面涂色的正方体》时，很多老师都用教学课件，展示了3面涂色、2面涂色和1面涂色的小正方体位置。（如图18）

但这样的教学，其实只是填鸭式的展示，缺乏想象力的孩子可能还是没有懂。为了使学生真正感受到数学的魅力，老师专门制作了教具（如图19），让学生真正操作，真实体验，感受规律。

（2）适时留白，唤醒儿童内心觉悟

课堂的适时留白，能启发诱导学生思考，引导学生走进课堂，体验矛盾，让学生有发挥的空间，最后交流体会水到渠成，在讨论交流、辩论说理中发展思维。

例如，五年级上册《小数的意义》。

师：我们已经知道了一位小数表示十分之几，两位小数表示百分之几，三位小数表示千分之几……你能任意写一个小数，然后在直线上写出来吗？  （如图20）

在认识小数的意义后，教师并没有在课堂上抛出很多练习，而是抛出问题，给学生留足时间和空间，让学生思考、交流，在找一个又一个数的过程中知道数的意义、位置、顺序等信息，犹如文章的布局谋篇，一气呵成。在这样的学习中学生才能去品尝到成功的喜悦和升华到美的境界，让课堂显得更充实，更有生机。

3.朝向学生发展驶向“远点”

数学教学的本质是要让学生学会数学地思维，教师要能够站在更高的层次上去引导学生的思维方向，把课堂的温度建立在思维的深度上，增设思维孵化的契机，让学生在思维演变的路上慢慢孵化、生长，向“通过数学学会思维”的方向发展。

如，教学一年级“100以内的数”一课时，“九十九添上一是多少？”通常情况下，教师引导学生从一个十，二个十，三个十，类推往下数，九十九，就是9捆小棒再多9根，再加1根就需要把9根合起来再捆成一捆，并且有10捆捆成一大捆，就是一個百。也可以这样教：在学生数一个十，二个十……的时候，对应的出现一个水滴，按顺序排好，直至九个十，十个十是一个百。（如图21）

这样的教学，可以引导学生明白数的排列顺序，也隐含了数轴的雏形，渗透了物数对应以及数的大小、无限性等，为后续知识的学习指明了方向。可以引导学生在享受劳动成果的过程中，对数学学习产生一份积极的情感，其活动积累的体验会使学生获得学习数学、建构数学思想方法的后劲。

理解文本，寻求教法，基于学生，这样“三线相融”式的教学，使教师的眼光不局限于教材，而是站在数学学科本质的高度去教学。正是这样的教学，才能使学生真正进入课堂，沉入课堂，使学生的数学思维得到深度发展，把学生真正带到知识和思维的更高处。

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]戴俊.“约定”未必“俗”成——数学约定性知识的教学意旨[J].中小学数学（小学版），2014（12）.

[3]庞舒勤.源流式教学：赋予数学知识自然生长的力量[J].江苏教育（小学教学版），2012（4）.

[4]匡金龙.数学课堂：让知识自然生长[J].江苏教育（小学教学版），2013（9）.

[5]包晓燕.简约至真：课堂教学就是一幅中国画[J].小学教学研究（教学版），2019（4）.