小学数学深度学习的认识与落实

课堂教学方法的深度研究

策划人语 教学改革，首先应是课堂的改革;课堂改革，首先应是教学方法的改革，课程教学方法是教育教学研究亘古不变的主题。

课堂教学方法有很多，先学后教、翻转课堂、以学定教……无论是哪种课堂教学方法，它的目的都是促进学生的学，让学生站在课堂正中央，让学科核心素养落地生根。

近年来，“深度学习”被越来越多的教师们所认识所理解所推崇，逐渐意识到只有深层次的学习才是有意义有价值的学习，才能真正培育学生的学科核心素养。本期，我们特别约请了人教版数学教材主编王永春、“全国小学数学深度学习研究联盟”理事长赵国防、全国著名特级教师黄慧共同探究“深度学习”，他们就概念厘清、相关认识和实践策略等进行了深入研究，相信能给广大教师带去一些思考和启迪。

（本刊编辑部）

【摘要】本文从小学数学核心素养的认识和落实两个维度进行讨论。从小学数学核心素养目标达成的视角对深度学习进行了界定，小学数学核心素养体系具体包括：数学认知（包括概念、命题、结构）、数学基本思想和关键能力、独立思考和自主学习、合作乐学。小学数学深度学习的落实重点包括：  加强学生对数学概念和命题的理解、加强知识间的自主关联和结构化，学习方式上强调以自主学习为主的多种教学方式的融合、非智力因素的协调发展。

【关键词】深度学习 核心素养 关联 结构化 学习方式

一、对深度学习的认识

关于深度学习，简明扼要地说，就当前对小学数学学科而言，学生达成数学核心素养目标的学习就是深度学习。笔者对小学数学核心素养的基本观点，已经发表文章进行了阐述，主要观点是超越数学学科本身来构建小学数学核心素养体系，具体包括：小学数学核心素养体系是以数学认知（包括概念、命题、结构）为基础，以数学基本思想和关键能力为核心，以学生的独立思考、自主学习、合作乐学为关键。其中，数学认知是对数学基础知识和基本技能的具体化，既是数学思想与能力的基础和载体，又是一个形成和运用数学思想、实现个人发展的心理活动和数学认知结构形成的过程;独立思考和自主学习是学生达成深度学习的核心途径和方法。形成数学核心素养的终极目标是实现个人发展、会用数学思想面对现实世界。

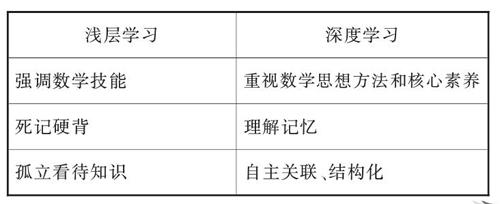
深度学习是一个相对的概念，是针对浅层学习而言的，从对数学本质的认识、学习方式、教学过程、课时知识容量、学习兴趣习惯等维度考虑，深度学习与浅层学习的比较如下表。

二、深度学习的落实

深度学习是从学生的角度论述的，体现了以学生为主体的教学理念。我们要实现深度学习，一方面需要教师具备这样的理念与专业素养;另一方面，在明确努力方向和目标的前提下，还要确定实现深度学习的方法和途径、评价标准等问题。独立思考、自主学习、合作交流等，这些既是个人发展的具体外在表现，又是实现个人发展的方法途径，综合来说是实现深度教学和深度学习的重要策略。关于自主学习，本来是各种学习方式（听讲、独立思考、自主学习、合作交流、动手实践等）其中的一种，那为什么强调自主学习呢？笔者认为，基于自主学习的学习，才是可持续发展的深度学习，所以应成为核心的学习方式。一方面，对学生而言，自我认识的觉醒与自主行为习惯的形成是学生发展的内因，比什么都重要，这样才能够学会学习、学会思考，形成可持续发展的态度和能力。另一方面，对教师而言，要认识到这样一个高度：学生核心素养的形成、自我成长能力的形成，仅仅依赖教师的讲授是不行的，更重要的是依赖学生自主学习、独立思考、合作交流，这是一种过程性的教育。实事求是地说，我们要构建实现深度教学和深度学习的教学范式，是以自主学习为核心、多种学习方式融合的基本教学方式，而不是只有自主学习这个唯一的方式。

1.强调对概念和命题的理解，没有理解就没有深度学习

学生对知识的理解水平决定对知识本质的接近程度，是进一步掌握和应用知识的基础，也是对知识进行分析与综合、评价与创造的基础。虽然深度学习不仅仅是反对死记硬背和机械模仿、强调理解基础上的记忆这么简单，但是理解是基础，没有理解这个根基其他免谈。概念既是基本思维，又是形成命题和推理的基础，没有正确的概念，就没有思维的材料，也就没有正确的判断，继而就没有正确的推理，也就没有进一步的思维。笔者把这个关系概括为：概念不清、判断不明、推理不灵。例如，长方形和正方形的认识，教科书并没有给出定义，只是让学生在一些多边形中，先辨认出长方形和正方形，学生通过上述一系列活动，初步抽象概括长方形和正方形的各自特征。考虑到部分学生的认知困难，回避了正方形是特殊的长方形，但是这种回避，丧失了一次认识概念的本质特征的机会，因为正方形满足长方形概念的本质特征，所以正方形也是长方形，只不过它比较特殊的是：四条边都相等。当学生真正建立了长方形与正方形的概念及关系后，才有利于后续知识的学习，才能够根据长方形的面积公式、正方形是特殊的长方形进行推理，推出正方形的面积计算公式。

2.用联系的、而不是孤立的观点处理知识，强调关联与结构化

深度学习不仅仅是一个知识点纵向深度，还有知识的宽度，各个知识点间的关联和结构化。浅表的碎片化知識不如深度的碎片化知识有价值，但是深度的碎片化知识不如深度的结构化知识有价值。比如，我们非常注重让学生记忆一些概念、公式、性质、运算律等，这固然重要，但是理解记忆比关联结构化更重要。在看到知识点间区别的同时，多看联系，这样有利于知识结构化，把概念结构化有利于保持长久记忆，减少记忆量。

以自然数的认识为例，学生从一年级到五年级（因数与倍数）一直在学习自然数。小学数学中自然数的本质是十进位值制，主要有两点：10个数字符号与数位。自然数中最重要的数是10，10是第一个发生质变的数，1到2，2到3，…，8到9，都是量变;而9到10是质变，10没有用新的符号表达，而是用了前面的两个数字符号1和0占用不同的位置（数位）表达，这个历史进程非常漫长。10的教学，可以启发学生进行时光穿越，回想我们的祖先（2600年前的春秋战国时期）如何数数计数：1个物体用“|”表示，2个物体用“‖”表示，3个物体用“|||”，…，9个物体用“”表示（阿拉伯数字在我国推广正式使用才100多年），那么比9个多一个，用什么表示呢？学生也可能想象：可以继续用不同的符号表示，但是这样下去，有很多物体时，就得使用更多的符号，很麻烦，也不容易记忆。那么，怎么办才能解决用比较少的符号表示很多数呢？请同学们开动脑筋，想出好办法来。勤劳智慧的中国人受个、十、百、千、万等这些计数单位的启发，创造了数位（位值制），只用10个符号就能够表示所有的数，把数字放在不同的位置上，可以表示不同的数。例如数字1，把1放在个位上表示1，放在十位上就表示10……可别小瞧这个发明，我们的祖先在商朝时期（大约公元前1600年）的甲骨文中开始用十进制计数，到春秋战国（大约公元前600年）发明十进位值制，这个过程用了近1000年。

学生理解了两位数10，其他两位数就水到渠成了。进一步，学生知道了9到10是怎么增加变化的，99到100也自然呼之欲出了，以此类推，999到1000，9999到10000，…，数位不断增加，只用10个数字符号和数位就能表达我们需要的数。十进位值制是读数、写数、比较大小、计算等的原理和依据。比如，两个数怎么比较大小？为什么数位多的数就大？两位数最大是99，三位数最小是100。数是一个一个大起来的，每当一个数位上是9时，再加1就进入下一个高位。以此类推，最大的n位数比最小的n+1位数小1。所以，两个数比较大小，数位多的数大。同理，如果两个数的数位相同，就先比较最高位。

现行教材单元后的整理与复习，强调了知识的关联与结构化。例如，《多边形的面积》单元后的整理与复习第1题（如下图），体现了知识之间的关联与转化、结构化。

但是这样还不够，这种关联与转化、结构化不能仅仅是事后诸葛亮，而更应该体现在知识的学习过程中，在每个知识点的学习中都应该不断地关联与转化、结构化。

3.强调独立思考、自主学习

我们的数学课堂教学和学习，要解决一个普遍性难题：为什么很多学生课堂上听懂了，但是不会做题？为什么作业会做了，考试题不会做？从理解到运用、应用的鸿沟是什么？如果教师讲、学生记，然后刷题，这样的教学没有真正体现学生的主体性，学生缺少独立思考和自主学习，无法达成深度学习。应培养学生独立思考、主动关联建构、自主变式探究、运用数学思想方法的能力和习惯。

比如，学生学习了除法、分数、比这三个概念，知道了它们的区别。但是另外一方面，更为重要的是，我们要看到这三个概念之间的密切联系和相同点，即这三个概念的符号表达形式可以用等号连接起来，建立等式，这样便于我们运算和推理，包括推导它们的性质。商不变的性质、分数的性质、比的性质、分式的性质，这四个知识点类似，具有可类比性。学生在四年级学习商不变的性质，通过计算几个具体的除法算式，运用不完全归纳法发现这几个除法算式有一个共同点：被除数和除数同时乘上或除以一个非零的数，商不变。等学习了分数的基本性质以后，可以用分数的性质推导商不变的性质、比的基本性质、分式的性质，而不必再用不完全归纳法探索规律，而是与分数的性质进行类比，直接把新知识转化成旧知识，完成认知结构的更新。这个转换过程蕴含了变中有不变的思想、恒等变形方法、数形结合思想（几何直观）、关联思想（普遍联系）、类比推理方法、转化思想等。

再如，学生学习了相遇问题后，应理解路程除以时间，得到的是两个速度的和。举例来说，一段1000米的直线路程，两个人从两端同时出发相向而行，如果两个人的速度相等，那么相遇时每个人只行了这段路程的[1] [2]，每个人用的时间是自己独立走完这段路程所用时间的[1] [2]。生活中还有类似的例子：在一条双向两车道的公路上，相距1千米的两辆汽车都以60千米/小时的速度相向行驶，两车多长时间会车？1÷（60+60）×3600=30（秒）。从答案中可以看出，两车会车的时间很短，如果两车相距500米，那么会车的时间只有15秒。这道题的现实意义在于：在双向两车道的公路上，超车一定要谨慎，要留出会车的安全距离;两辆汽车都以60千米/小时的速度相向行驶，相当于对方汽车不动，而自己以120千米/小时的速度冲向對方。

4.兴趣、态度、习惯、自信心、价值观等方面应协调发展

学生个体的数学认知结构主要包括：个体的数学知识结构、数学思想方法、元认知、非智力因素等。非智力因素虽然不直接参与智力活动，但是对智力或者思维的影响不可小觑，比如说有的学生平时数学考试成绩非常好，但是一到期末考试或者中考、高考就发挥失常。这是非智力因素的影响，影响学生对认知结构中数学知识的提取（本来是储存在头脑中的，状态不好时提取不出来，等到状态正常时又恢复了），以及智力活动和思想方法的运用。因此，培养学生对数学学习的兴趣、态度、习惯、自信心、价值观等就显得尤为重要，而且各方面应协调发展。

这里我们要特别强调的是，从一年级开始就培养学生自主学习的能力，加强对数学本质的理解，如前文所述，加强学生对自然数，尤其是10的本质的认识，这是学生能够长期建立对数学的兴趣、好感、自信心的根本保障。当然，并不是说情境、活动、游戏不重要，而是要通过这些情境、活动、游戏让学生感悟数学的本质，否则部分学生早晚对数学失去兴趣与信心，三年级的两极分化就是一个残酷的现实。