改进傅里叶方法在梁结构振动特性分析中的应用

肖 伟，霍瑞东，李海超，高晟耀，庞福振

（1.中国舰船研究设计中心，武汉 430064；2.哈尔滨工程大学 船舶工程学院，哈尔滨 150001； 3.中国人民解放军92578部队，北京 100161）

梁结构在工程领域中应用广泛，开展典型梁结构振动特性研究具有重要的价值。在此方面，Rao[1]得出了一般约束下Euler-Bernoulli梁的振动频率和振型。ABBAS[2]使用有限元法求解得到了Timoshenko梁的自由振动方程。Grief[3]提出使用拉格朗日方程的基于傅里叶级数的振动模态方法。在此基础上Chung[4]综合利用傅里叶级数和拉格朗日乘子，提出了一种在经典边界条件下梁的固有频率和模态计算方法。W.L.LI[5]提出了一种改进傅里叶级数的方法，该方法在传统傅里叶级数方法的基础上增加了一项辅助多项式函数，成功解决了梁在边界上存在的不连续性问题。张大克等[6]针对梁的振动方程采用了广义差分法进行求解。许士菊等[7]采用有限差分法求解到了精度较高的振动模态数值解。曾文平等[8]则运用多辛算法推导求解了等截面梁的自由振动特性。

通过对国内外研究现状的分析可知，现有的梁结构振动特性分析方法大多局限于经典边界条件或某些特定的弹性条件，对一般边界条件下的振动问题研究较少。为此，本文基于改进傅里叶级数法，建立了弹性边界条件下梁结构振动分析模型，并基于弹簧参数法模拟一般边界条件，在保证良好收敛性的前提下具有较高的求解精度，可为一般边界条件下梁结构振动特性分析提供参考依据。

1 梁结构模型的建立与求解

在研究梁结构的弯曲振动问题时常用的物理模型主要有Euler-Bernoulli梁、剪切梁、Rayleigh梁和Timoshenko梁。其中，Euler-Bernoulli梁忽略了旋转和剪切变形因素，剪切梁模型在其基础上考虑了剪切效应，Rayleigh梁模型在其基础上考虑了截面旋转效应，而Timoshenko梁模型则同时考虑了旋转和剪切这两种效应，从而可得到最为理想的效果。

1.1 Euler-Bernoulli梁自由振动微分方程

本文取在一般边界条件下的Euler-Bernoulli梁为研究对象，其物理模型如下图所示

图1 一般边界条件下的梁结构示意图

其中：K0、K1表示旋转方向约束弹簧的刚度，k0、k1表示横向约束弹簧的刚度。

根据弹性力学相关知识，梁的动力平衡方程可表示为

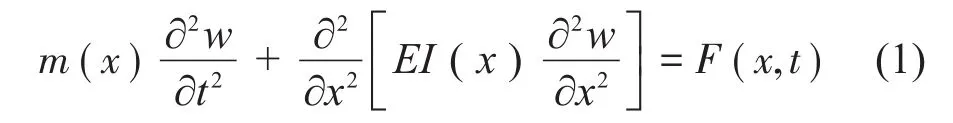
将梁视为均质等截面梁，在研究其自由振动时其外界激励载荷F(x,t)=0，则上式可改写为

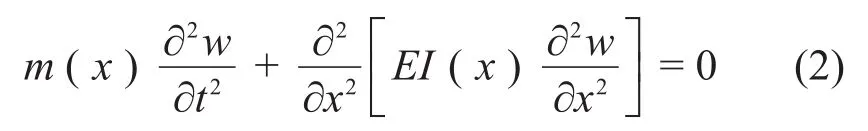
其中：I和E分别为梁的惯性矩和杨氏模量，w为梁的横向位移函数。

梁结构的边界条件可以表示为

其中：K和k分别代表旋转约束和横向位移约束弹簧刚度，通过改变弹簧刚度值可模拟不同边界条件下梁结构的振动情形，具体弹簧刚度取何值能有效模拟各种边界条件的讨论将在后文进行。

1.2 基于改进傅里叶级数的梁结构振型函数

根据改进傅里叶级数的方法，Euler-Bernoulli梁的振型函数可表示为

式中：Am和Bn是位移容许函数中未知的Fourier系数，λm=mπ/L，λn=nπ/L。引入简谐时间因子eiωt用于表述梁在不同时刻的位移函数。显然位移容许函数的选取将会直接影响到求解的结果，在求解过程中需将式（5）代入平衡方程式（1），但传统傅里叶级数的导数在端点处会产生不连续现象，如图2所示。

图2 传统傅里叶级数在端点处不连续问题示意图

通过将位移容许函数表征为式（5）的形式，即除了单傅里叶余弦级数以外，还包含一项单傅里叶正弦级数，该正弦项辅助函数的引入使位移容许函数满足求解域内2阶导连续且3阶导存在，从而有效地克服边界上可能存在的不连续性问题，如图3所示。

图3 改进傅里叶级数解决端点处不连续问题示意图

通过对位移函数逐次求导就可以得到速度、加速度等参数。因此整个求解过程的主要任务变为求解未知的傅里叶展开系数。

1.3 基于Hamilton原理的模型求解

首先对系统进行能量描述，分别求出该系统下的总势能V、总动能T以及外部载荷做功We，然后基于Hamilton原理求解得到梁振动的特征值方程。由于Euler-Bernoulli梁是最简单的梁结构模型，它忽略了旋转和剪切效应，因而其弯曲产生的应变能可表示为

相应地，系统的动能Tb以及弹簧的势能Vs可分别表示为

外部载荷所做的功可以表示为

其中：外载荷为均布载荷时用式(9)表示，外载荷为集中载荷时由式(10)表示。δ为单位脉冲函数，F为外载荷的幅值，x0表示作用点的位置。

因此，总势能可以表示为

于是，梁结构的拉格朗日函数可以表示为

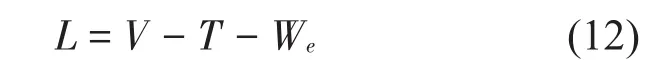
将式(6)－式(10)代入式(12)，并对未知的傅里叶系数求极值

联立上述两式，可得梁结构振动的标准特征式方程

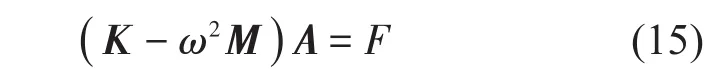
式中：K和M分别为系统的刚度矩阵和质量矩阵，其取值只与系统的结构特征和边界条件有关，当外载荷F=0时即可由求得梁结构自由振动下的振动特性。

任意激励下梁结构的傅里叶系数向量可表示为

将上式求解结果代入式(3)，即可求得梁结构的受迫振动特性。

2 方法有效性验证

为验证本方法的收敛性和计算结果的准确性，本文从弹簧刚度值、傅里叶展开阶数多个角度，定量分析影响本方法计算结果收敛性的因素。同时将本方法在几种典型边界条件下的计算结果与有限元计算结果及相关文献进行比对。

本文所研究梁结构模型的几何及材料属性参数如下：长L=1 m，截面宽b=0.06 m，高h=0.01 m，杨氏模量E=2×1011Pa，密度ρ=7 800 kg/m³，无量纲频率取Ω=L/π(ωρA/D)12。

2.1 弹簧刚度值对收敛性的影响

为了探讨弹簧刚度k、K如何合理取值以模拟各种边界条件，同时验证弹簧刚度对计算收敛性的影响，图4以C-C典型边界条件为例，显示了无量纲频率参数Ω与弹簧刚度值的变化关系。其中假设K0=K1=k0=k1。

图4 C-C边界条件下Ω随弹簧刚度值变化关系

从图4可以看出，在C-C边界条件下，无量纲频率参数Ω在弹簧刚度取到1×108之后趋于收敛，此时即可模拟刚固的边界条件，弹簧刚度在1×104～1×106区间内与频率值大致呈线性关系，结合结构固有频率应与材料弹性模量呈线性相关这一普遍规律，可将其视为弹性边界条件。此外从上图可以看出该范围两端的线性规律不如中间段明显，因此弹簧刚度值取中间部分来模拟弹性边界较为合理。如不做特殊说明，本文均取刚度值为1×1010来等效刚固条件，取1×105来等效弹性条件。在此基础上，图5讨论了C-S边界条件下，无量纲频率参数Ω关于横向弹簧刚度k1的收敛性。其中刚固端取K0=k0=1×1010，简支端旋转方向无约束，取K1=0。

从图5可以看出，在C-S边界条件下也有类似的规律，无量纲频率参数Ω在弹簧刚度取到1×108之后基本趋于收敛，因此用旋转方向弹簧刚度K=0、横向弹簧刚度k=1×1010来模拟简支条件是合理的。

为了探讨上述用于模拟各种边界条件所取弹簧刚度范围和梁结构刚度之间的关系，本文以C-S边界条件为例，给出了不同杨氏模量下1阶固有频率随横向弹簧刚度值k1变化的规律(见图6)，其中刚固端取K0=k0=1×1010，简支端取K1=0。

图5 C-S边界条件下Ω随横向弹簧刚度值k1变化关系

图6 不同刚度下Ω随横向弹簧刚度值k1变化关系

从图6可以看出，模拟不同边界条件的弹簧刚度取值范围与梁的刚度有明显关系，梁的刚度越大，相应的线性范围越靠右，即对于较大刚度的弹性梁应取较大的弹簧刚度值来模拟弹性边界条件。具体范围应通过试算来选取。

根据上述讨论，本文给出了刚度取E=2×1011Pa时，几种经典边界条件下弹簧刚度的合理取值，如表1所示。

表1 弹簧刚度取值

2.2 傅里叶展开阶数对收敛性的影响

傅里叶级数展开后所截取的阶数对计算结果的精确度有直接影响，展开阶数越多越接近准确值，但会影响求解效率。一般来说所取阶数达到一定值后计算结果即可趋于稳定，本文以C-C边界条件为例，探讨了本方法计算结果收敛性随展开阶数M变化的影响。

从表2可以看出，随着展开阶数的不断增加，梁结构无量纲频率参数逐渐趋于收敛，当M=10之后无量纲频率参数已具有较高的精度。因此本方法所求解的频率值关于展开阶数M收敛性良好，如不作特殊说明，本文展开阶数均取M=10。

表2 C-C边界条件下Ω与展开阶数关系

2.3 有效性验证

为了验证本方法计算结果的有效性，本文给出了几种典型工况下无量纲频率的计算值，并与有限元仿真结果及现有文献进行比对，有限元（ANSYS）分析模型参数与1.1节相同，单元类型为shell63，网格数量为47 926，对比结果如表3所示。

由表3可知，本文方法计算结果与有限元仿真结果具有较好的一致性，最大相对误差不超过0.11%，由此可证得本方法的有效性；从计算效率上来看，本方法只需修改对应弹簧刚度值即可模拟各种边界条件，在更换模型时只需修改对应尺寸参数与材料属性值，可见本方法相较于传统有限元法体现出了巨大的优势。本方法所求得C-C边界条件下梁结构自由振动振型图与有限元仿真对比如图7所示。

3 简谐载荷作用下的受迫振动响应

在对梁结构进行一般边界条件下自由振动模态分析的基础上，讨论了一定激励下结构的受迫振动响应特性。

其中梁的具体参数保持不变，激励载荷幅值取F＝1 000 N，扫频范围取f＝1 Hz～1 000 Hz。图8和图9分别给出了梁在刚固和弹性边界下梁中点位置处速度与加速度级的响应曲线，其中模拟弹性边界条件下的弹簧刚度值取：K0＝K1＝1×105N·m/rad，k0＝k1＝1×104N/m。

由图6可知，弹性边界条件下梁结构的波动程度比刚固边界条件大，尤其是在低频激励下这种情况更为明显，但相应的激励响应幅值却要小很多，此规律可为工程中的减振方案提供借鉴与参考。

为探讨弹性边界条件下旋转方向约束弹簧与横向约束弹簧刚度变化对梁振动特性的影响程度的区别，本文给出了一些对比性的数值结果。表4为对梁一端刚固，另一端分别改变旋转方向和横向弹簧刚度后梁的1阶无量纲频率值。

表3 经典边界下梁结构的无量纲频率参数

将表4的数值结果用三维图表示如图10所示。

图7 C-C边界条件下本方法与有限元结果振型图对比

表4 旋转方向和横向弹簧刚度变化对固有频率的影响

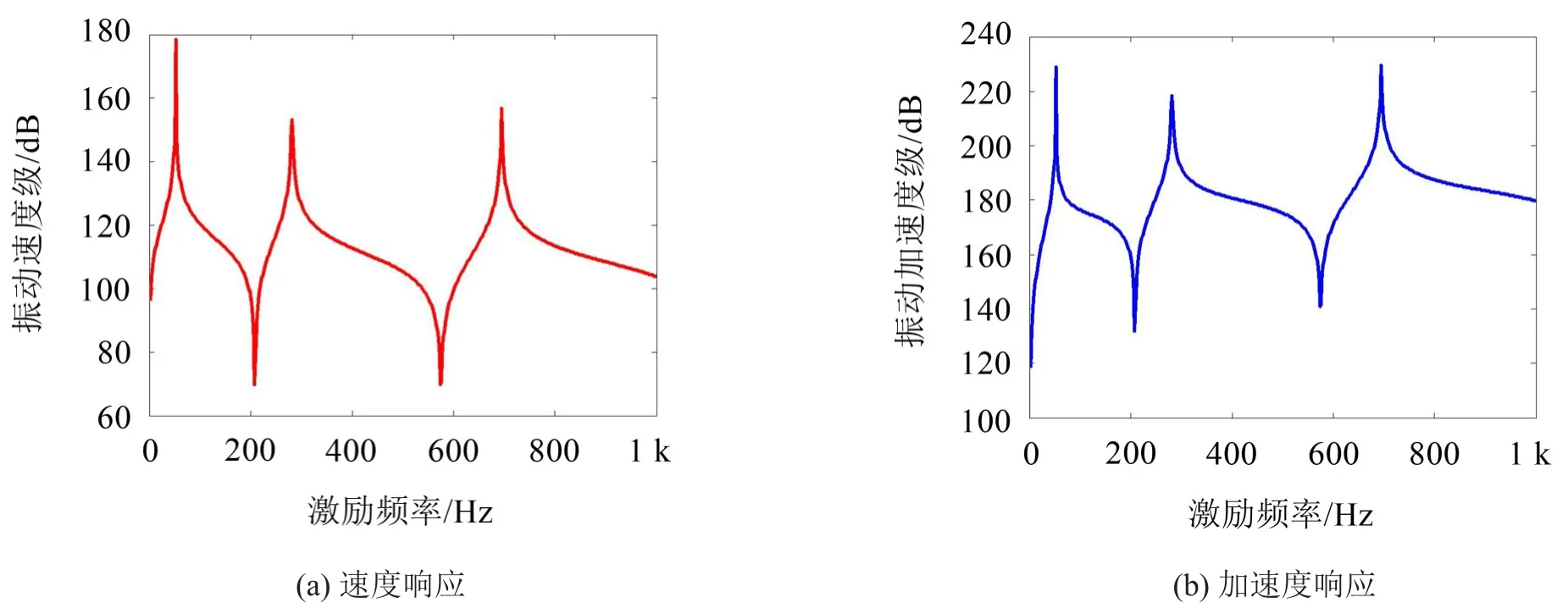
图8 刚固边界条件下梁中点位置处激励响应图

从图10中可以很直观地看出两者对梁振动特性影响程度的不同。当横向弹簧刚度k保持不变时，1阶无量纲频率随旋转方向弹簧刚度K的增大变化不很明显，而当旋转方向弹簧刚度K保持不变时，1阶无量纲频率随横向弹簧刚度k的增大变化很大，由此可知横向约束对梁结构振动特性的影响起主要作用。

图9 弹性边界条件下梁中点位置处激励响应图表1经典边界下的弹

图10 旋转方向与横向弹簧刚度对固有频率值的影响

5 结语

本文基于改进傅里叶级数法对一般边界条件下梁结构的振动特性进行了研究，通过本文研究，可得如下主要结论：

(1)通过计算分析并与有限元结果对比验证了改进傅里叶级数法的准确性与良好的收敛性。

(2)通过改变结构两端的弹簧刚度值可有效模拟一般边界条件，并给出了典型边界条件下弹簧刚度的合理取值。

(3)模拟不同边界条件弹簧刚度值的选取取决于梁的刚度值大小。

(4)针对梁的低频受迫振动，对梁进行弹性约束可更有效降低结构的振动响应。

(5)在弹性边界条件下，梁端横向约束对结构振动特性的影响比旋转方向约束大。