基于流固耦合的货车燃油箱动力学仿真分析及试验验证

程贤福，程安辉，李 晶，梁高峰

（华东交通大学 机电与车辆工程学院，南昌 330013）

燃油箱在实际使用过程中不仅承受来自地面的振动，还要承受因振动而引起的燃油晃动的冲击，而燃油的晃动又受到燃油箱的影响，是典型的流固耦合问题。流固耦合问题的研究在航空、汽车、水利、化工、海洋等领域都有着十分重要的意义[1-2]。装有燃油的油箱动力学特性和空油箱的动力学特性有很大的差别[3]，工程实际中如果不考虑流体的作用，往往会造成结构强度不够，噪声过大影响乘坐舒适性[4]，疲劳寿命达不到预期设计的目标[5]。随着对流固耦合问题研究的深入，各种不同的分析计算方法也相继被提出，其中有限元法是应用最为广泛的一种数值方法，是研究流固耦合问题的有效手段。其中程相克[6]等人通过对燃油箱干湿模态分析发现装入燃油后燃油箱的耦合模态频率大幅下降。张俊红[7]等人采用流固耦合方法对塑料机油冷却盖的振动噪声水平进行了预测评估，根据预测结果识别出对噪声贡献度较大的耦合模态频率。屠翔宇[8]等运用Opti Struct求解器计算油箱的自由模态。用Hyper View观察模态分析结果，得到前5阶固有频率和振型，并通过试验验证了有限元分析结果的准确性。王晖等[9]分析了储液容器液体深度变化对结构频率的影响，得到系统频率与水深关系曲线，考察了刚度对系统频率的影响。一般来说，主要有4种分析流体对结构作用的方法，分别是轴对称水弹性模型分析法、流固耦合法、虚拟质量法、外场法，流固耦合法适合于分析含液容器的模态分析和振动分析，是流体与结构耦合动力学分析的重要方法[10]。在工程振动领域有着重要的应用。梁高峰[11]运用流固耦合方法对燃油箱进行了2 g振动激励下的焊点应力分析。但未增加试验量级进行对比试验。

上述文献主要考虑了液体对燃油箱模态频率及变化规律的影响，对燃油箱耦合振动的力学响应分析较少。本文利用有限元仿真计算与试验相结合的方法对国内某公司自主研发的某轻型货车的油箱进行不同充液比（燃油与燃油箱的总容积之比）的湿模态仿真，分析不同充液比固有频率和振型的变化规律。在路试中发现0.5充液比状态下的燃油箱更容易发生破坏，因此在模态分析分析的基础上利用国标规定的振动谱作为振动输入，重点对0.5充液比的油箱模型进行振动分析。

1 流固耦合基本理论

1.1 流体离散方程

由欧拉方程、连续方程、伯努利方程及拉普拉斯方程联合推导得出可压缩流体连续方程为

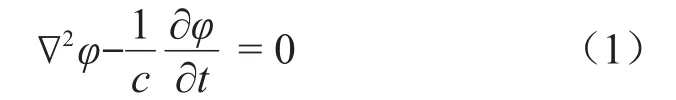
式中：∇为拉普拉斯算子，c为声音在液体中的传播速度，φ为流体速度势函数，φ=φ(x,y,z,t)是2阶连续并且可导的。求解φ还需要确定边界条件，其边界条件为：

1）流体与固体耦合交界面SI上

式中：n为流固交界面处的法线方向。

2）固体界面SB上

3）液体自由液面SF上

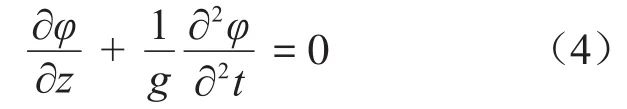
式中：g为重力加速度。

通过Galekin法推导流体运动的离散方程为

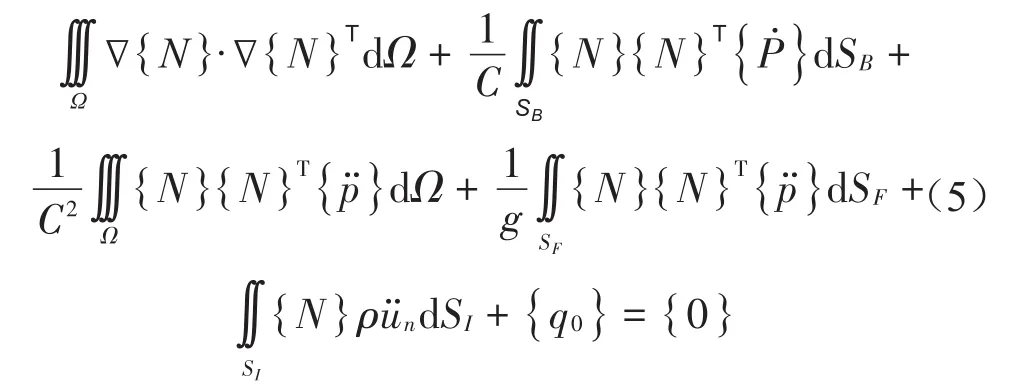
式中：{N}为流体单元的动压力的形函数向量；{P}为流体单元的动压力方向向量；n为箱体在耦合交界面上的法向加速度；ρ为水的密度；Ω为整个流体域；{q0}为已知输入激励向量或给定的边界运动向量，其中包括了由于结构变形而引起流体的位移向量。

将式（5）写成矩阵和向量的形式

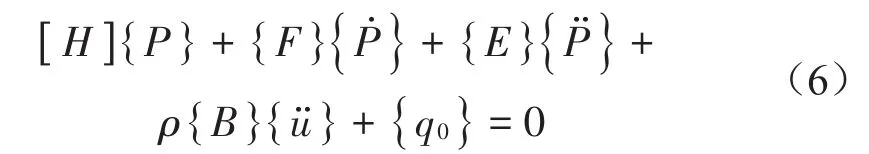
式中：{u}节点位移向量；

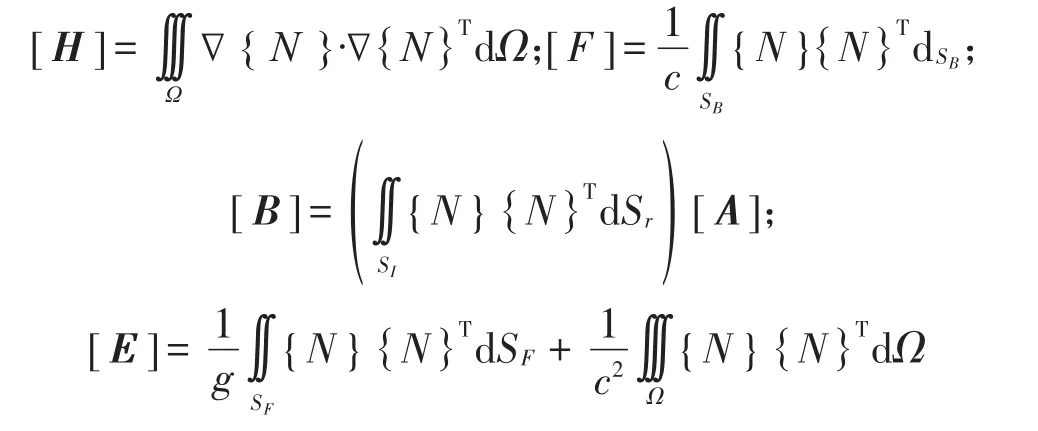
1.2 燃油箱结构离散方程

1）结构的受力平衡方程

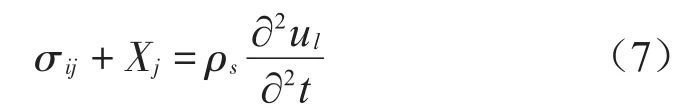
式中：σ代表应力；Xj代表体积力在三个坐标方向的分量；ul是位移矢量。

2）几何方程

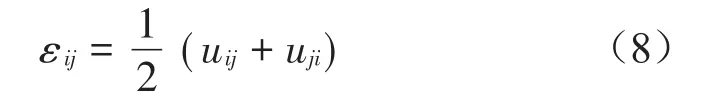
式中：ε表示应变，uij、uji为位移矢量。

3）物理方程

式中：E为弹性模量。

4）边界条件

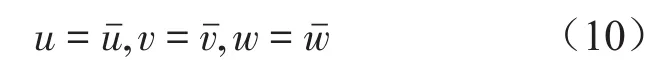
式中：u、v、w分别代表任意一点的位移矢量在坐标X、Y、Z方向的分量，、、代表对应u、v、w的单位表面处位移。

根据哈密尔顿变分原理建立离散结构单元的运动方程

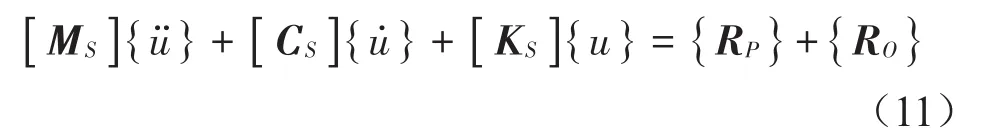
式中：[MS]为质量结构矩阵；[CS]表示振动结构阻尼矩阵；[KS]代表振动结构的刚度矩阵；{RP}、{RO}分别为流体和固体交界面处流体作用在结构上的动压力向量和作用在结构上的其他动载荷向量。

1.3 流固耦合系统离散方程

结合以上方程，利用虚功原理可以得出流体和固体耦合系统离散方程为

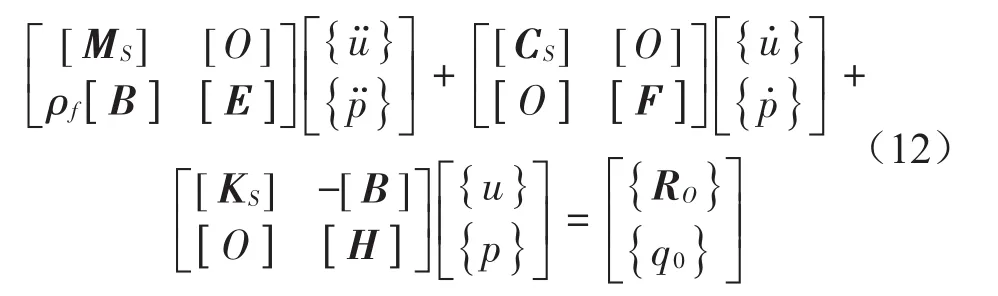
2 模态分析

油箱的振动不仅影响发动机供油系统的稳定性，而且还影响到油箱的使用寿命。因此了解油箱的固有频率和振型，可为防止油箱发生共振破坏、振动疲劳以及评价油箱结构的动态特性和优化结构设计提供一定的依据[12]。通常模态分析都是在密度较小的空气中进行的，空气对模态分析结果影响不大因而不考虑空气的作用，将这种条件下的模态分析称之为干模态分析。对于内部含有液体的燃油箱而言，会受到液体的作用而且液体的密度比空气大很多，液体与固体的耦合作用在模态分析时需要考虑在内，这种考虑耦合作用的模态称之为湿模态分析。通过对油箱湿模态分析，提取相应的固有频率和振型，为振动分析奠定基础。

2.1 油箱模型及固定方式

在进行有限元分析前，首先建立油箱的三维模型。本文的油箱三维模型是在SolidWorks中完成的，如图1所示。

图1 燃油箱三维模型

托架通过螺栓固定在车架上，箱体的固定是通过箍带固定在托架上。油箱的固定方式对模态分析结果和振动分析结果都有很大的影响，为了能够真实反映计算结果，需要在托架上添加固定约束。

2.2 模型简化说明

利用ANSYS进行燃油箱模态和振动分析需要对模型进行合理简化，综合考虑模型的复杂程度和网格数量以及计算结果精度，对模型做出如下简化：

1）忽略箱体上一些对计算结果影响较小的附件包括：铭牌、油量传感器、吸油管固定支架、螺纹加油管、连通管、放油螺栓等。

2）不考虑燃油箱的装配工艺的影响，即箱体与端板和防波板的点焊连接对箱体材料性能没有影响，将箱体、端板、防波板以及箍带和托架视为一个整体。

3）除箍带和托架外将箱体、端板和防波板视为厚度均匀的薄壁。

4）假设液体没有粘性，不可压缩的理想液体。

分别建立简化后的空油箱模型如图2(a)中所示、含有25%燃油的燃油箱模型如图2(b)中所示、含有50%燃油的燃油箱模型如图2(c)中所示、含有75%燃油的燃油箱模型如图2中(d)所示。

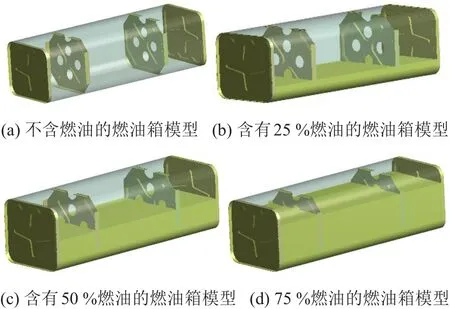
图2 简化后的燃油箱模型

2.3 材料参数

本文研究的燃油箱采用BFS-400材料冲压而成，其材料参数为：弹性模量2000 MPa，泊松比为0.3，密度为7 850 kg/m3，箱体以及隔板的厚度均为0.8 mm；

利用水代替燃油，其密度为1 000 kg/m3，声音在水中的传播速度为1 500 m/s。

2.4 网格划分与求解方法设定

定义流体的单元类型为流体声单元，自由面处定义膜单元。为了使流体与固体在交界面处实现网格节点对应，将燃油箱与内部的流体定义多体部件。将固体单元与流体单元交界处用FSI命令标记为流固耦合交界面。因为流固耦合问题是通过非对称矩阵求解的，因此定义模态的求解方法为非对称法。

2.5 求解频率范围确定

为了减少运算的盲目性和计算机计算规模，合理确定燃油箱的共振频率范围是十分有必要的。燃油箱的直接激励来源于车架，而车架的激励由发动机振动和路面不平产生。发动机产生振动的原因是发动机点火（压燃）曲轴脉冲式输出扭矩、连杆和曲轴往复式运动而产生不平衡惯性力。

曲轴脉冲式输出扭矩产生的振动频率计算公式为

式中：n为发动机转速（r/min）；i为发动机气缸数；τ为冲程系数，两冲程取值为1，四冲程取值为2。

不平衡惯性力产生振动频率计算公式

式中：Q为比例系数，一级惯性力取值为1，二级惯性力取值为2。

本文所研究燃油箱用于6缸柴油机供应燃油，该柴油发动机参数如下：怠速转速850 r/min，冲程数为4。由于曲轴通常安装平衡块来平衡连杆和曲轴往复式产生的惯性力，因此发动机的振动主要是曲轴脉冲式输出扭矩产生的振动。经计算发动机的振动频率为42.5 Hz，考虑到弹性阻尼橡胶悬置的减震作用，本文模态频率计算从30 Hz开始。

2.6 有限元分析结果

模态分析的目的是揭示液体的存在对模态频率的影响及变化规律，由于车架的频率较低，对油箱的振动起主导作用的是低阶模态，因此分别提取模型的前12阶模态如表1所示。

由于不同状态下的油箱模态阶数较多，一一展示会占用较多篇幅，因此本文给出了空油箱的前6阶模态（第6阶模态的频率已经远远超出车架的振动频率）变形云图，如图3所示。从前6阶模态变形云图可以发现，燃油箱的变形区域主要集中在箱体的上表面，与文献8得到的分析结果一致。

表1 干湿模态固有频率/Hz

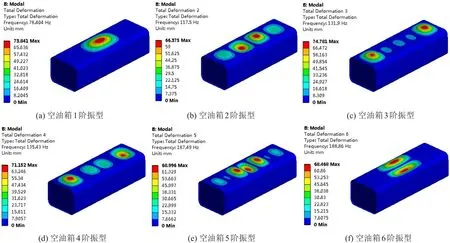
图3 油箱前6阶模态

模态频率随阶数的变化曲线如图4所示。

从图4可以看出湿模态与干模态的固有频率相比有明显的下降，其中充液比从0%～50%燃油的模态下降得更加明显，但是随着燃油充液比的进一步增大，充液比到50%以后模态下降幅度缓慢且各对应阶数模态下降也缓慢，所以含75%以上的燃油模态不再分析。原因是油箱在晃动时燃油对箱体有粘附作用，在流体与固体的相互耦合作用下使得整个分析对象的湿模态的频率小于干模态的频率。随着燃油量的增加，整个分析对象的质量增加，造成整个分析对象的模态频率下降。

3 振动分析

3.1 振动激励输入

一个振动系统结构振动频率不能与所在环境相适应[13（]燃油箱固有模态频率与车架频率相等），否则会产生共振，导致噪声过大，严重时发生防波板脱落，箱体被撕裂现象。因此有必要对燃油箱进行振动分析。

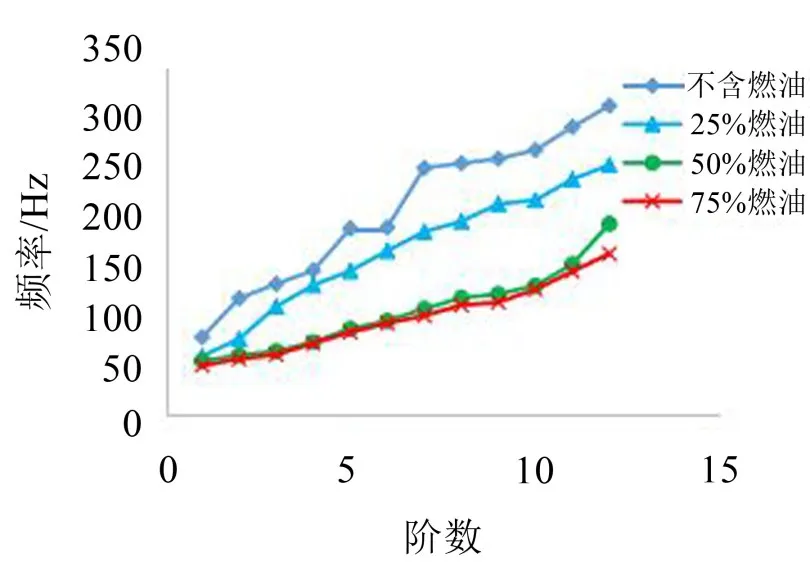
图4 模态频率随阶数变化曲线

在前文模态分析的基础上根据国标GMW3172_AUG2008对燃油箱固定在装置上进行随机振动谱的规定，其振动频率以及加速度如表2所示，对应的振动曲线图如图5所示。并将该振动曲线作为ANSYS随机振动分析的激励。

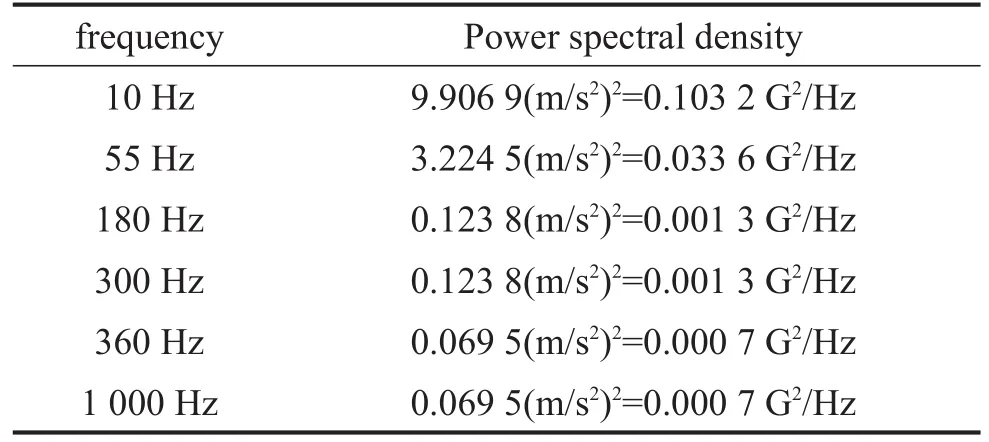
表2 随机振动频率对应加速度表

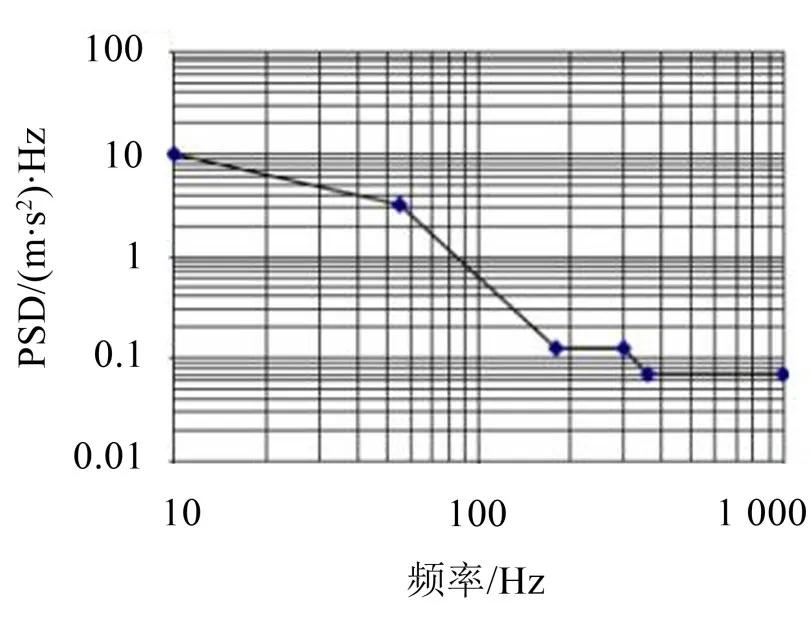
图5 随机振动曲线

3.2 试验设计

为了验证分析结果的准确性，将燃油箱放置在MPA409/LS444A/GT800M振动台上进行试验并在相应的位置布置传感器利用DEWE-2601采集仪采集实验数据，由于燃油箱在实际使用过程中中间两块防波板与箱体连接处（通过点焊连接）容易发生破坏，因此此处是仿真和实验关注的重点。将此处以及与其对称处各布置一个应变片，同时将两端各布置一个应变片用于应力数据的提取。燃油箱安装状态如图6所示。在本实验中，利用40 kg水代替箱体内的燃油，随机振动方向定义如图7所示。对油箱的3个方向进行随机振动试验，从应力的测量结果判断最严酷的试验方向，之后在严酷方向上依次增加试验量级，增加步长为2 g，进行对比试验。

图6 燃油箱安装及传感器的布置图

图7 随机振动方向定义

3.3 数据分析

随机振动的激励在振动时间内的相位与幅值无法进行准确的预测，但是随机振动概率概率密度函数能够通过解析式表达，一般认为具备高斯分布（正态分布）的特征[14]。随机振动的激励信号具有很强的不确定性，在任意时刻都有全频率带宽内的频率存在。但可以通过对随机信号功率谱密度、标准差等指标对进行评价。高斯随机振动信号加速度瞬时值分布在{-3σ，+3σ}区间分布的概率为99.73%，约为1，瞬时峰值超过3σ值的概率非常小。因此工程上通常认为随机信号的最大加速度激励水平为3σ（1 σ为试件加速度响应的均方根植）即随机振动激励下的峰值，在仿真应力分析时提取了3σ下的应力。由于2#和3#应变片是燃油箱内防波板与箱体的点焊所在位置，且两者处于对称位置，因此在实验和仿真过程中，重点提取了2号应变片位置处的应力数据。

车辆在行驶过程中，会受到纵向、横向以及垂向3个方向的振动，因此对燃油箱的3个方向分别进行了仿真分析和随机振动试验。在垂向方向上2#应变片处的试验应力为63.77 MPa，在仿真软件中提取焊点处的应力为60.18 MPa，如图8、图9所示，两者数值比较接近，误差为5.6%。

图8 垂向2#应变片仿真应力

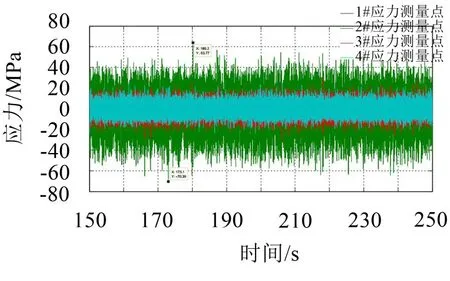
图9 垂向2#应变片实验应力

在横向方向上，2#应变片处的试验应力为83.15 MPa，在仿真软件中提取焊点处的应力为82.07 MPa，如图10、图11所示，误差为1.3%。

在纵向方向，试验得到的应力的数值40.12 MPa，在仿真软件中提取的该处的应力为42.22 MPa，如图12、图13所示，两者的误差为5.23%。

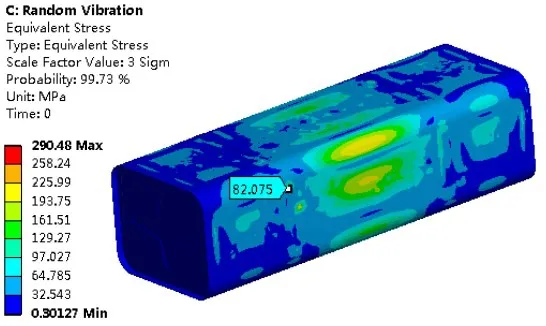
图10 横向2#应变片仿真应力

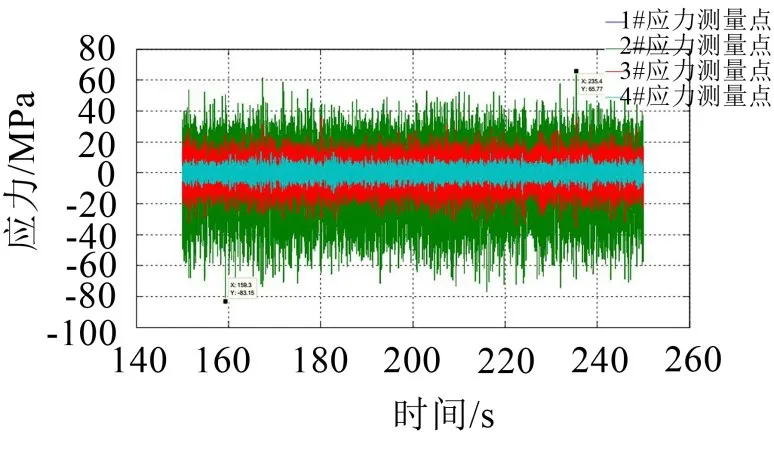
图11 横向2#应变片实验应力

图12 纵向2#应变片仿真应力

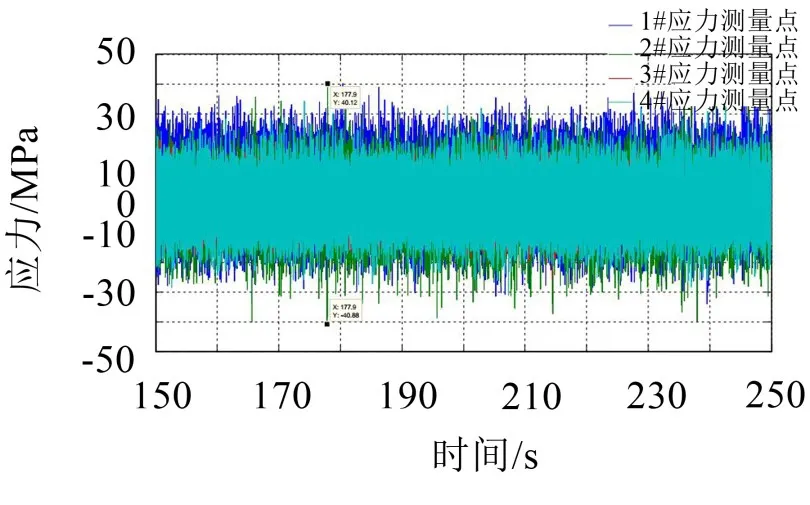
图13 纵向2#应变片实验应力

从纵向、横向以及垂向3个方向的应力数值看，横向的应力数值最大，其确定为严酷方向。在严酷方向上依次增加试验量级，增加步长为2 g，在试验和仿真过程中，分别提取2号应变片位置处4 g、6 g和8 g的应力数据进行再次对比试验。对比试验数据如表3所示。

由于在箱体内还有吸油管、连通管、滤网、固定螺栓等结构，进行有限元仿真时，除隔板外全部将其简化，导致在纵向方向液体所受的阻力减小，使得仿真得到的应力大于试验应力。

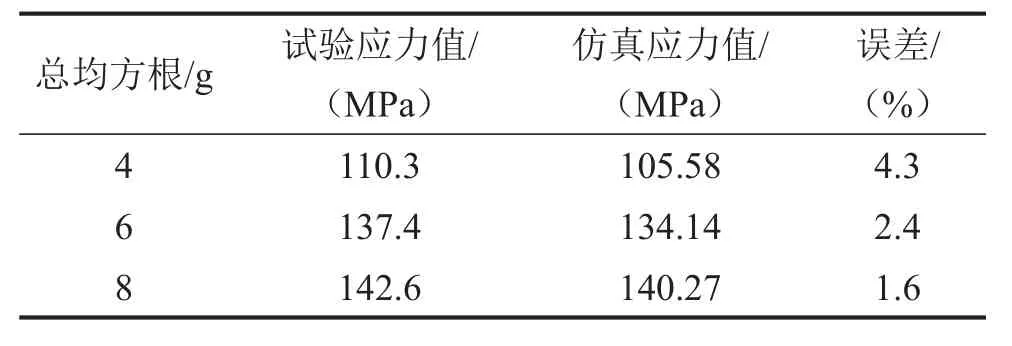
表3 不同总均方根下试验和仿真应力值

通过对3个方向及严酷方向的应力分析发现，虽然应力分析结果在各个方向上有不同程度的误差，但是误差均在6%以内，能够满足工程分析要求。

4 结语

（1）建立不同充液比的燃油箱模型，通过模态计算发现与空油箱相比，含有燃油的油箱模态频率较低。随着注油量的增加，模态频率曲线随阶数增加变的平缓。

（2）利用国标对燃油箱振动谱的规定对含有50%燃油的燃油箱进行了振动仿真，在仿真软件中提取相应位置的应力，通过横向、纵向、垂向3个方向及严酷方向的应力与实验应力对比发现，误差较小，符合工程设计要求。

（3）该仿真方法能够对贮箱类流固耦合的模态、振型和振动响应进行分析和计算。

（4）对不同充液比油箱进行了模态分析，获得了充液比对模态频率的影响规律，进行了燃油箱随机振动仿真与实验研究，通过对比特定位置应力值仿真结果与试验测试结果，验证了仿真分析的准确性。论文研究方法具有一定的工程参考价值。