一种管道卡箍位置自动优化方法

於为刚，赵正大，陈 果，寸文渊，陈雪梅，侯民利

（1.南京航空航天大学 民航学院，南京 210016；2.成都飞机工业（集团）有限责任公司，成都 610092）

管路系统作为现代飞机动力传输的主要通道，承担着输送燃油、滑油、空气和液压油等介质的重要任务，因此在飞机的运行过程中起到极其重要的作用[1]。然而，飞机液压系统管路的振动问题一直困扰着工程技术人员。随着现代军用飞机对作战性能的要求日益提高，飞机液压系统逐渐向高压力发展，工作压力可以达到21 MPa，甚至28 MPa，管道振动问题也随之愈加突出。对管道的振动抑制可以采取多种方式，包括管形优化、卡箍优化、以及施加管道减振器等[2]。

安装卡箍是增加管道系统刚性、减小变形、避免低频共振的一种主要方式。目前，飞机管道系统中卡箍的布置多是从原型机中对比和移植，再依靠设计者的经验在实际放样时做出一定的调整，这样会造成实际卡箍布局具有较大的随机性，严重影响了管道系统的可靠性，使飞机产生一定的安全隐患[3]。因此，研究复杂管道系统的卡箍位置优化方法具有极其重要的意义。

Wang分别以变形最小化和基频最大化为目标，采用启发式优化算法实现了对直梁结构和矩形板结构的支撑位置和优化设计[4-5]；Zhu等采用伪密度技术将离散问题转化为连续体建立支撑布局的拓扑优化方法[6]；刘伟分别以基频与外界激振频率的差值最大化以及随机振动均方差响应最小化为目标，利用罚函数法对复杂管路的关键卡箍位置进行了优化设计[7]。李鑫以激振源固有频率点的特征阻抗加权和为目标函数，利用粒子群优化算法为飞机液压管路的优化布局提供了一定的理论依据[8]。

然而，现有研究方法复杂度较高，计算效率很低，难于满足工程实际的需求。有鉴于此，本文确定以提高管路系统基频为目标，提出了一种新的基于模态位移的管道卡箍位置自动优化方法，并进行了方法验证。

1 管道系统模态分析理论

在对管道进行模态分析时，不考虑阻尼和外载荷的影响，管道系统的自由振动方程方程是

其中：M和K分别为管道系统的质量矩阵和刚度矩阵。设自由振动响应为以下形式

代入无阻尼自由振动方程可得

通过求解上述方程可以确定ω和X，其中特征值ω1,ω2,……,ωn代表系统的n个固有频率，特征向量X1,X2,……,Xn代表对应每一阶固有频率ωi的n个固有振型。

2 卡箍位置的灵敏度分析

安装卡箍是增加管道系统刚性、减小变形、避免低频共振的一种主要方式，卡箍位置与刚度对系统振动特性有着重要的影响。为了研究卡箍位置和刚度对管道固有振动特性的影响，针对某一空间管道，获得管道在施加不同位置和刚度卡箍下的基频变化，并基于卡箍位置对提高管道基频的灵敏度分析，得到卡箍位置与刚度对管道基频的影响规律，进而确定卡箍优化的最佳位置。

建立的空间管道有限元模型如图1（a）所示，由4根直管和3段弯管构成。导管具体尺寸为：Pipe1=530 mm，Pipe2=930 mm，Pipe3=520 mm，Pipe4=880 mm，外径为21 mm，壁厚为2.4 mm。导管密度设为7 850 kg/m3，杨氏模量为2×1011N/m2，泊松比为0.3。该导管被离散为22个单元，共计23个节点。

（1）两端为固定支撑的情形

设S1和S2为管道两端的固定支撑点，分别布置在节点1和节点23。为了最大程度地提高管道基频，需要研究卡箍位置对提高管道基频的灵敏度，得到管道施加卡箍的最优位置。对该支承情形下的管道进行模态分析，管道基频为12.21 Hz，第1阶振型如图1（b）所示。

图1 管道模态分析

图2为第1阶振型中各个节点的无量纲振型位移。为了得到卡箍位置对管道基频的影响规律，选择在不同位置施加不同刚度的卡箍，表1和图3都表示了在不同位置和刚度卡箍下的基频变化情况。从计算结果可以看出：

1）在无量纲振型位移最大的节点施加卡箍能最大程度地提高基频，是施加单个卡箍的最优位置；

2）当卡箍的刚度在达到某个值时（卡箍刚度在106N/m以上），再增加卡箍刚度对管道基频无影响，即可以认为是固定支撑。

（2）三点固定支撑的情形

在两端固定的情形下得到最优卡箍位置为第1阶振型位移最大处，在该处（节点12）设置1个固定支撑S3，即设定已经优化好的卡箍，卡箍刚度为108N/m，如图4（a）所示。对3点固定支撑下的管道进行模态分析，管道的基频为30.26 Hz，第1阶模态振型如图4（b）所示。为了进一步提高管道基频，需要继续增加卡箍，现在需要解决如何以最少的卡箍最大程度地提高管道基频的问题。

表1 卡箍不同位置和刚度下的管道基频/Hz

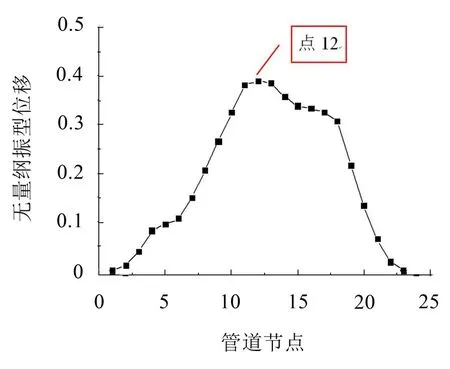
图2 第1阶振型位移

图5为第1阶振型中各个节点的无量纲振型位移，从振型图中可以看出，在3个固定点间出现了2个极大值点。

根据2点固定下的管道分析结果，可以设想，要想进一步最大程度地提高管道基频，可以在每2个卡箍固定点间的振型位移极大值点处施加1个卡箍，即在3个固定点下需要同时施加2个卡箍。

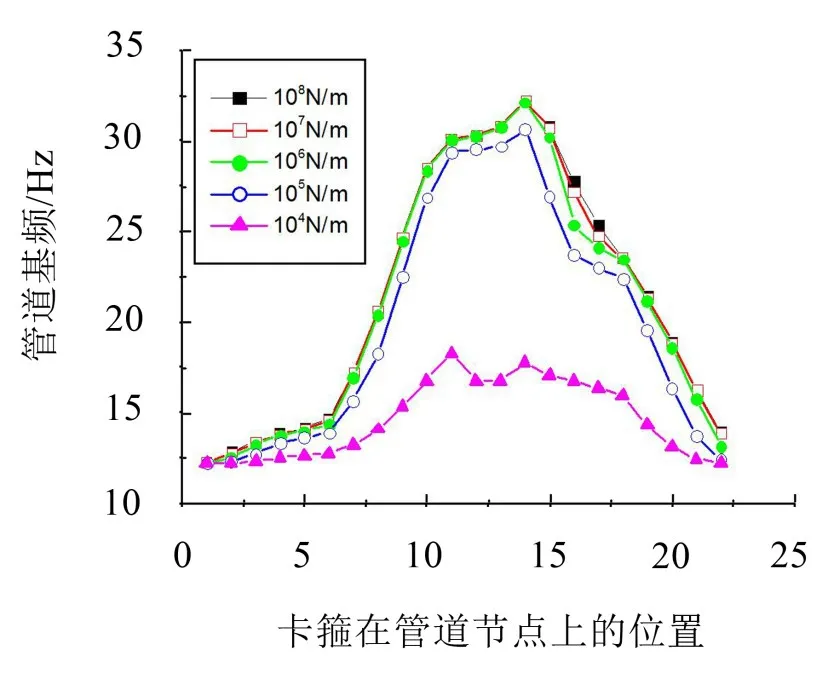
图3 不同卡箍位置和刚度下的管道基频

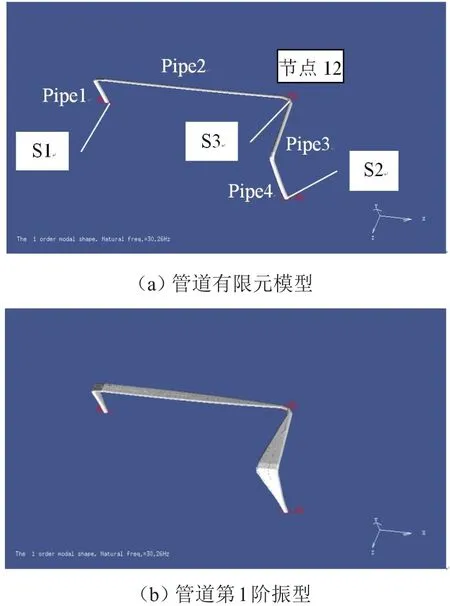
图4 管道模态分析

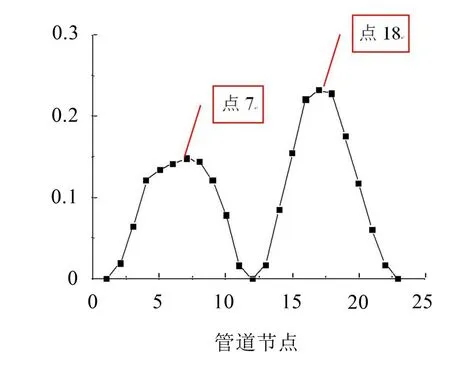
图5 第1阶振型中各个节点的无量纲振型位移

为了验证这一想法，计算比较了在不同位置同时施加两个卡箍的管道基频，其中1个卡箍加到节点2到节点11之间，另一个加到节点13到节点22之间，卡箍刚度设定为108N/m。

表2为不同卡箍位置和刚度下的管道基频。从计算结果可以看出：3点固定不加卡箍时，基频为30.26 Hz；3点固定施加2个卡箍时，管道基频最大提高到110.67 Hz，卡箍位置正好对应于第1阶振型位移的2两个极大值点，分别为节点7和节点18，这与设想中提出的卡箍最优位置完全一致。由此，可以得出结论： 22个固定间点的模态位移极大值点是进一步提高管道基频的最优卡箍位置点。

3 基于模态分析的卡箍优化方法

根据上述卡箍位置对提高管道基频的灵敏度分析，得到卡箍位置对管道基频的影响规律：两个固定间点的模态位移极大值点是进一步提高管道基频的最优卡箍位置点。基于此规律提出了1种管道卡箍位置自动优化方法，其基本流程框图如图6所示。主要步骤为：

（1）导入给定初始固定支撑位置的初始管道模型；

（2）通过模态分析得到管道系统的基频及对应的第1阶振型；

（3）判断基频是否达到目标值，如果达到则输出卡箍位置、数量及管道基频；如果没有达到，则在第1阶振型的极大值点处施加卡箍，得到新的管道模型；

（4）转入步骤2，计算新的管道模型，直至管道系统的基频满足要求。

4 卡箍优化方法验证

为了验证管道卡箍位置自动优化方法的正确性，选择了《GJB 3054-1997飞机液压管路系统设计、安装要求》中针对特定管型给出卡箍施加的最优位置进行对比。该要求中提到：流速突变会在管路系统中产生冲击压力，换向阀快速切换会产生大的冲击压力，作动筒活塞快速止动时也会引起液压冲击。冲击压力在导管中以音速传播，当压力传到导管转弯处就产生1个侧向力，使导管弯曲，并使导管承受弯曲应力，弯曲成U型和Z型的导管受影响较大。一些固定不良的管路系统，当产生液压冲击时会发生大的导管位移和振动。如图7所示。

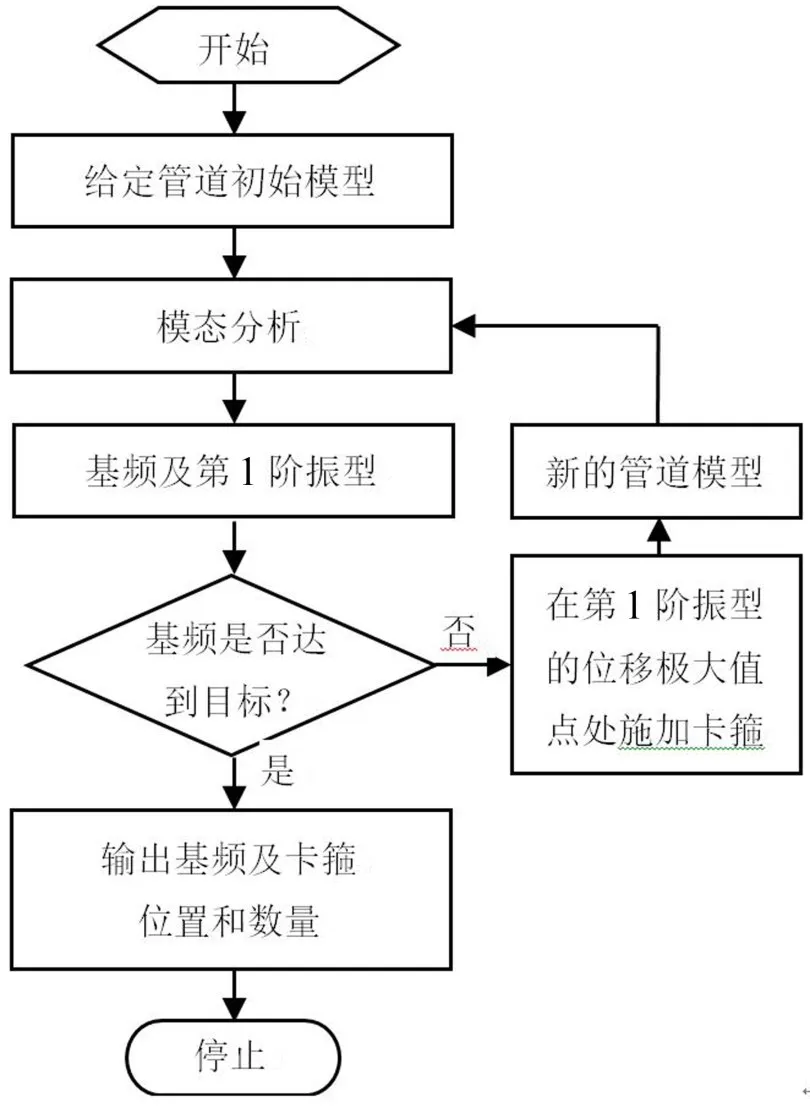
图6 管道卡箍优化流程

图7 GJB 3054-1997飞机液压管路系统设计、安装要求

仅在C处设置管夹难以阻止导管运动，衬垫易磨损，导管也易受损，应继续在A或B设置管夹。

4.1 Z型导管分析

根据图7（a）建立一段Z型管道有限元模型，导管各段长度如图8（a）所示，L1=0.5 m，L2=0.35 m，L3=0.5 m，导管外径为20 mm，壁厚为1 mm。导管密度设为7 850 kg/m3，杨氏模量为2.07×1011N/m2，泊松比为0.3。导管两端设置为固定支撑，将导管离散为42个单元、43个节点。

图8 Z型管道分析与优化

图8（b）和表3为优化结果，从表3可以看出，在不加卡箍时，管道基频为47.79 Hz，第一次优化结果为在节点22处施加一个卡箍，基频提高到149.78 Hz；第二次优化结果为在节点13和31再各增一个卡箍，基频提高到354.11 Hz。与图7（a）对比发现，卡箍优化结果与GJB 3054-1997中提到的Z型管道卡箍设置结论相同，验证了卡箍优化方法的正确性与有效性。

表3 Z字形管道卡箍优化结果

4.2 U型导管分析

根据图7（b）建立一段U型管道有限元模型，导管各段长度如图9(a)所示，L1=0.5 m，L2=0.35 m，L3=0.5 m，导管外径为20 mm，壁厚为1 mm。导管密度设为7 850 kg/m3，杨氏模量为2.07×1011N/m2，泊松比为0.3。导管两端设置为固定支撑，将管道离散为42个单元、43个节点。

图9 U型管道分析与优化

图9（b）和表4为优化结果，从表4可以看出，在不加卡箍时，管道基频为33.83 Hz，第一次优化结果为在节点22处施加1个卡箍，基频提高到149.79 Hz；第二次优化结果为在节点13和31再各增一个卡箍，基频提高到354.72 Hz。与图7（b）对比发现，卡箍优化结果与GJB 3054-1997中对U字形管道的卡箍设置结论相同，验证了卡箍优化结果的正确性与有效性。

表4 U字形管道卡箍优化结果

5 结语

（1）基于卡箍位置对管道基频的灵敏度分析研究了卡箍对基频的影响规律，以提高管道基频为目标，提出了一种基于管路系统模态位移的卡箍位置自动优化的方法。

（2）利用GJB相关规范中的Z形和U形管道进行了方法验证，结果充分表明了新方法的简便性和有效性。