弹性边界条件下弹性基础加筋板声辐射特性研究

孙勇敢，黎 胜，包振明

(1.大连理工大学 工业装备结构分析国家重点实验室 运载工程与力学学部船舶工程学院，辽宁 大连 116024；

(2.重庆交通大学,重庆 400074； 3.江苏科技大学,江苏 镇江 212003)

加筋板结构在建筑、车辆和海洋工程等领域得到广泛的应用，其声学性能一直是国内外学者研究的重要课题。在实际结构中，如土木建筑的楼板，高速公路，具有弹性车轮的轻轨车辆甲板等通常可以简化为具有弹性基础的板/加筋板结构等。国内外学者在弹性地基结构动力问题方面开展了大量的研究工作，Morfidis[1]推导了铁木辛柯梁在弹性基础上的动力平衡方程及相应的固有振动方程，B.Uğurlu等[2]研究了弹性基础和流体对矩形板固有频率和振动模态的影响，Hashemi等[3]应用里茨法研究了流体加载下弹性基础矩形板动力特性，计算了不同的弹性基础刚度、流体加载区域，边界条件，几何尺寸下结构的固有频率。Nguyen[4]研究了移动质量激励下弹性基础梁的动力响应，覃霞等[5]运用最小二乘无网格法研究了弹性地基上加筋板的固有频率，高阳等[6]建立了被隔振设备弹性基础上受垂向激励的力学模型，结果表明设备弹性基础对整体的弹性振动不能被忽略，贺小龙等[7]建立了弹性基础下多级并联调谐质量阻尼器数学模型，讨论了弹性地基对主系统的影响。这些研究表明弹性基础对结构的静力或动力性能有重要影响，而弹性基础对结构的声学性能研究却比较少，另外，而实际结构边界约束往往比较复杂，如船舶甲板结构的边界既不是自由支持，也不是刚性固定，而是介于自由支持和弹性固定之间的情况，因此，本文对弹性边界条件下弹簧基础加筋板声学性能进行研究。

1 弹性边界条件下弹性基础加筋板声辐射特性计算模型

考虑结构与流体的耦合效应，弹性边界条件下弹性基础加筋板在外力作用下有限元形式的运动方程为[8]

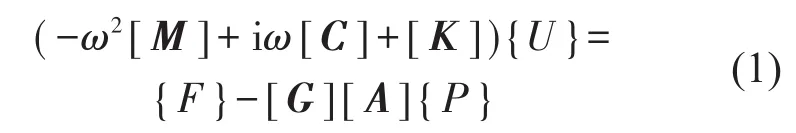
其中：[M]，[K]=[Ks]+[Kf]+[Kb]和[C]分别是总体质量矩阵，总体刚度矩阵，总体阻尼矩阵。其中[Ks]为加筋板刚度矩阵dS为弹性基础刚度矩阵，[N]为板结构形函数矩阵，弹性基础仅与垂向位移有关[9]，Γ为加筋板的边界，[N(b)]为弹性边界形函数，弹性边界Kb包括旋转刚度Kr和Z方向的平移刚度Kt。ω为激励圆频率，{F}为外载荷向量，{U}结构节点位移向量为转换矩阵，{P}为结构表面声压向量。

结构表面辐射声压和节点法向速度的关系为

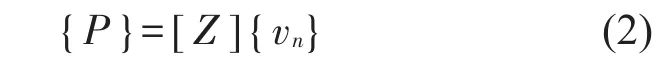
式中：[Z]为声阻抗矩阵，可由带无限障板的板表面进行瑞利积分求得，{vn}为结构表面节点的方向速度向量。结构表面节点法向速度向量{vn}与节点速度向量{v}之间的转换关系为

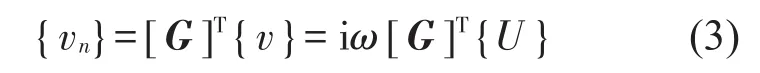
联立式(1)－式(3)，未知结构位移向量可用以下公式求得

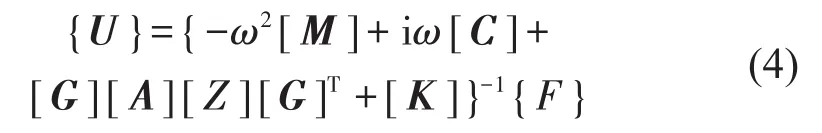
一旦结构位移向量求出，结构表面声压和节点法向速度可有式(2)－式(3)求出。

结构的辐射声功率可以用结构表面声压和节点法向速度表示，即

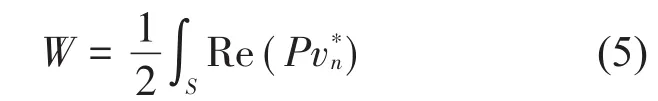
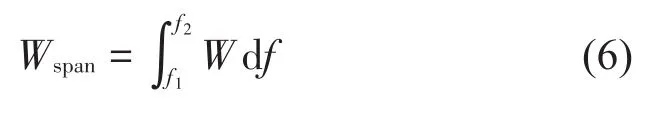
在某带宽范围内辐射的总功率为其中f1和f2为起始频率和终止频率。

结构表面法向速度均方值定义为

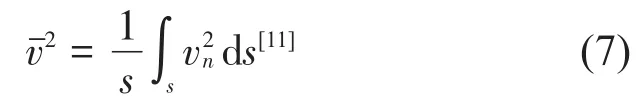
声辐射效率为

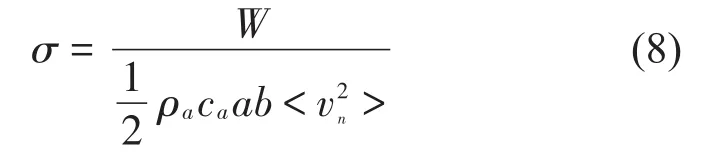
式中：ρa为流体密度，ca为声速，a为板长，b为板宽。

2 数值结果分析

图1为工程中常见的加筋板结构，选取如图中所示的坐标系，在计算中取板的尺寸为：板长a=0.8m，板宽b=0.6m，板厚h=0.01m，T型材尺寸为（单位：mm），L型材尺寸为20× 15× 4（单位：mm），材料为钢,杨氏模量E=2.1×1011N/m2，泊松比ν=0.3，密度为ρ=7800kg/m3。Kf为弹性基础刚度，Kt为z方向边界支持刚度，Kr为边界旋转刚度，不同的边界旋转刚度和边界支持刚度的组合可以表示相应的边界条件。结构阻尼比取值1%，流体介质为空气，密度ρa=1.21kg/m3，声速为ca=343m/s，参考声功率10-12W，单位简谐力作用在加筋板的中心位置。

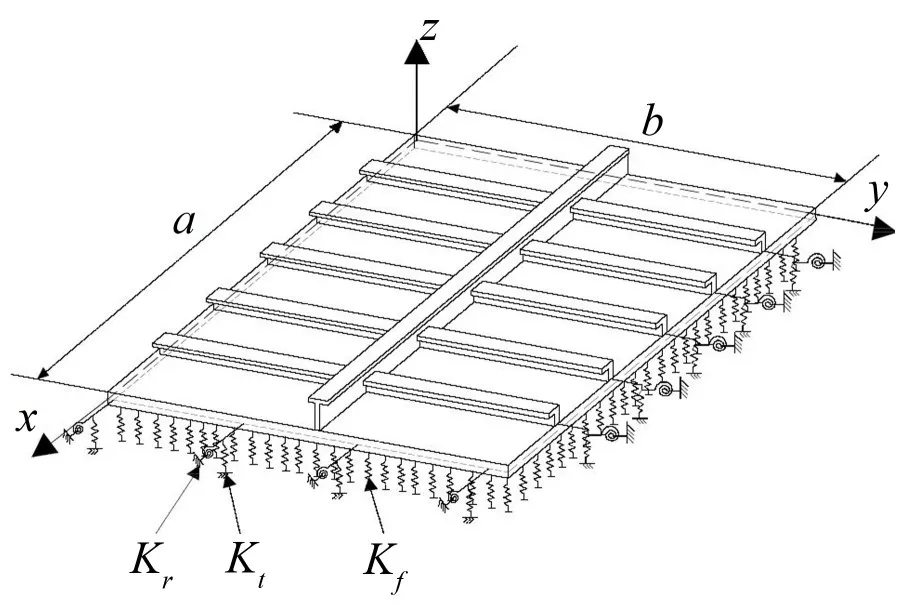
图1 具有弹性边界加筋板模型

2.1 模型验证

下面分两步验证本文计算模型的精确度，首先通过计算弹性边界和弹性基础条件下板的固有频率来验证弹性边界刚度和弹性基础刚度的精度，再通过计算矩形板辐射声功率特性验证计算模型的可靠性。

2.1.1 验证弹性边界条件和弹性基础条件下板固有频率

令式（1）中等式右边等于零可求出加筋板在真空中的固有频率。为计算C-F-F-F边界条件且x=a和y=a边界处分别具有平移约束刚度和旋转约束刚度方形板[12]，将本文计算模型中T型材和L型材取为微小值（下同），y=0边界处取支持刚度和旋转刚度为无穷大表示刚性固定边界，x=a处的平移约束刚度1a3=100，y=a处的旋转约束刚度分别取b1a=10和b1a=100，其中x1=Kt/D，b1=Kr/D，D表示板的弯曲刚度，计算时网格为48×48，计算结果与文献[12]比较见表1，可以看出结果非常接近。

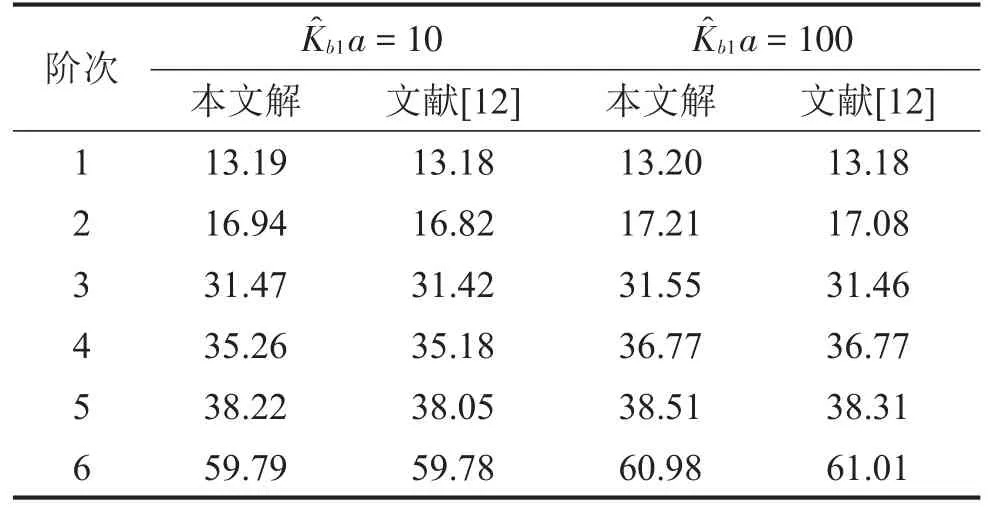
表1 C-F-F-F边界约束且x=a和y=a边界处的分别具有平移约束刚度和旋转约束刚度方形板的频率参数，kx1a3=100

弹性地基板[13]，板长a=1 m，板宽b=1.2m，板厚h=0.02m，杨氏模量E=7.2×1010N/m2，泊松比ν=0.3，密度为ρ=2800kg/m3。Kf=5.5N/m3，计算时四周边界处支持刚度Kt和旋转刚度Kr取为无穷大表示刚性固定边界，计算时网格为48×48，计算结果与文献[13]比较见表1，可以看出结果相差较小。

表2 四周刚性固定弹性地基矩形平板的前5阶频率/Hz

一四边刚性固定的钢板[14（]a=b=1m，h=0.025m），单位简谐力作用在板的中点。计算时四周边界处支持刚度Kt和旋转刚度Kr取为无穷大表示刚性固定边界，Kf=0N/m3，计算结果与文献[14]比较见图2。可以看出结果非常接近。

2.2 边界条件对加筋板振动特性的影响

为方便讨论，加筋板四周边界采用相同的约束且弹性基础刚度系数Kf=0N/m3。图3为加筋板固有频率随边界支持刚度和边界旋转刚度变化（或自由边界—简支边界—刚性固定）曲线，从下到上依次是前10阶的固有频率，从图中可以看出存在固有频率急剧增加的2个阶段，第1个阶段：边界支持刚度从Kt=1×106Pa变化到Kt=1×109Pa，边界支持刚度对高阶频率的影响较大，而对低阶频率的影响较小，弹性模量（弯曲刚度）增加（减小）时，第1阶段所对应的边界支持刚度也近似线性增加（减小）（图4（a）），故产生第1个阶段的原因是，与加筋板弯曲刚度相比，边界支持刚度足够大时（约Kt=1×106Pa）能够限制加筋板边界节点的垂向位移，边界支持刚度增大时，结构的刚体位移和边界节点位移逐渐变小，当Kt=1×109Pa时，结构模态变为四周边界位移约为零的弯曲振动模态（图5），此时即使再增大边界支持刚度，结构模态也将不会改变；第2个阶段：边界旋转刚度从Kr=1×105N/rad 变化到Kr=1×108N/rad，加筋板的固有频率也会有所增加，但没有第1阶段增加的幅度大，各阶频率变化基本相同，弹性模量增加（减小）时，第2阶段所对应的边界旋转刚度也近似线性增加（减小）（图4（b）），故产生第2个阶段的原因是，与加筋板弯曲刚度相比，边界旋转刚度足够大（Kr=1×105N/rad），能够限制弯曲振动模态的边界转动，边界旋转刚度增大时，结构模态边界的转角逐渐变小，当Kr=1×108N/rad时，结构模态为四周边界转角约为零的弯曲振动模态，此时再增大边界旋转刚度，结构模态将不会改变。在其他边界支持刚度和边界旋转刚度范围内，加筋板的固有频率基本不变。

2.1.2 验证矩形板辐射声功率

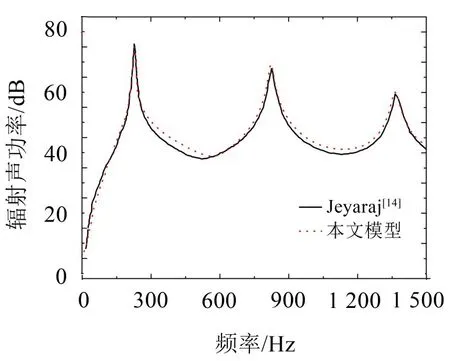
图2 与文献[14]矩形板辐射声功率对比

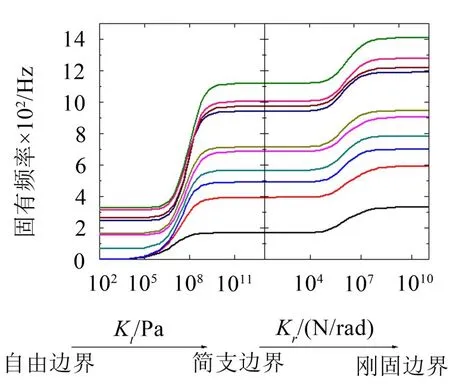
图3 边界支持刚度和边界旋转刚度不同时加筋板前10阶固有频率变化曲线

当边界支持刚度较小时，为避免刚体位移的影响，以边界支持刚度取不同的值时加筋板的第7阶模态为例来具体说明边界支持刚度对加筋板模态的影响，如图5所示（其他阶次变化类似不再赘述），从图中可以看出边界支持刚度增加时，加筋板的模态发生了明显变化，主要原因是边界支持刚度的增加限制了边界节点位移，与图3加筋板频率突变阶段相对应，在此阶段边界支持刚度对结构模态有较大影响。

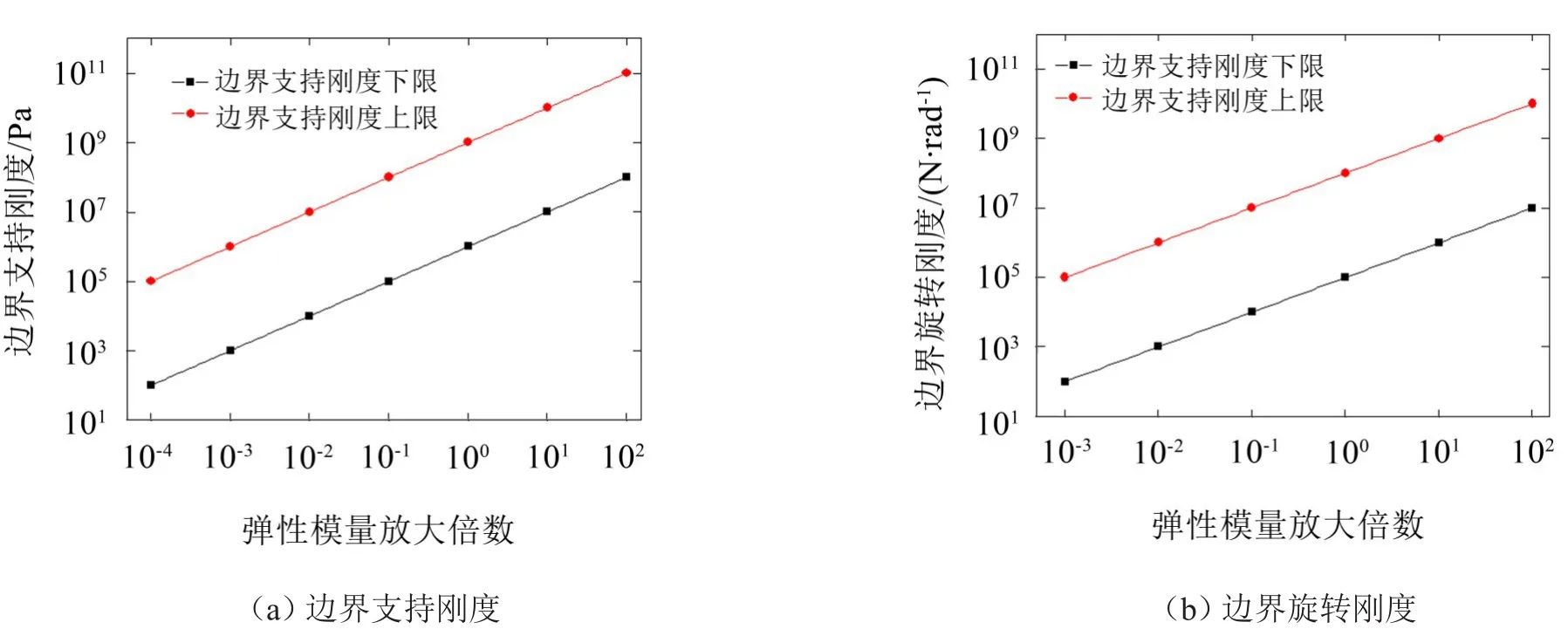
图4 不同弹性模量时加筋板固有频率增加阶段所对应

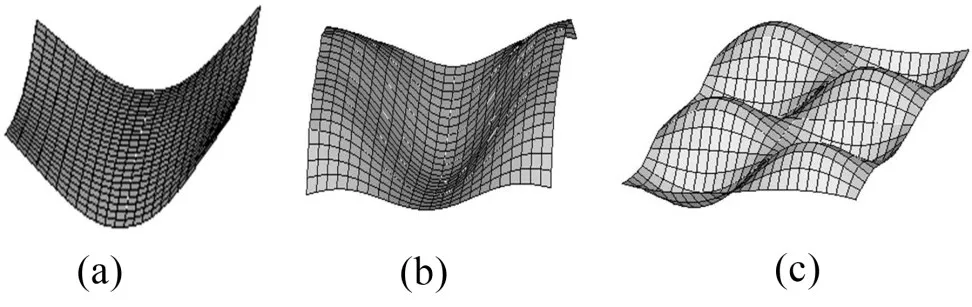
图5 不同边界支持刚度时加筋板的第7阶模态

当边界支持刚度足够大时，增加边界旋转刚度，此时结构模态因变化较小不易观察，为了清晰地描述边界旋转刚度对加筋板模态的影响，以y=b/2时加筋板的线模态为例具体说明边界旋转刚度对模态的影响。图6为边界旋转刚度取不同的值时加筋板的前两阶模态，从图中可以看出边界旋转刚度增加时（箭头方向表示边界旋转刚度增大），加筋板模态基本不变，仅模态两边的“坡度”略变小。由此可见，支持边界刚度比旋转边界刚度对结构模态的影响更大。

2.3 结构参数对加筋板辐射声功率特性的影响

2.3.1 边界支持刚度的影响

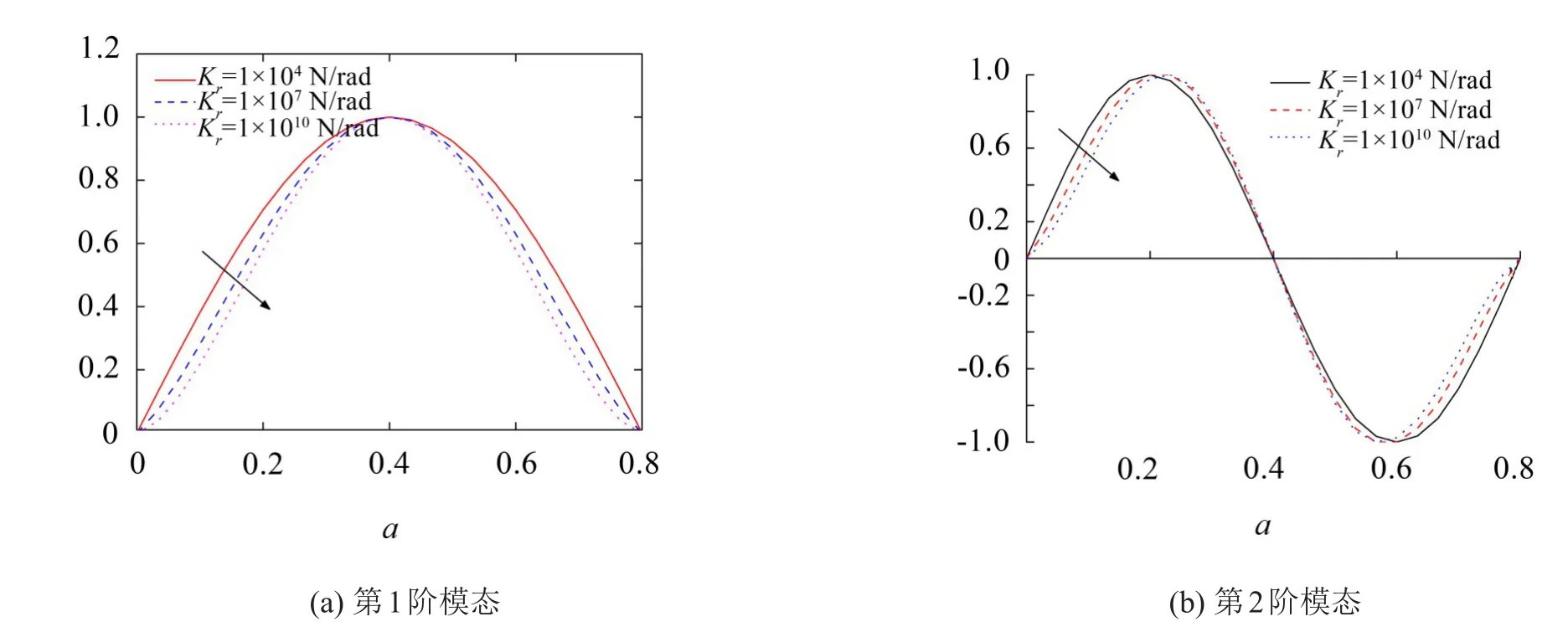
图6 在y=b/2处加筋板的模态

板结构辐射声功率与结构表面各点的振动幅值和振动速度的分布有关，而结构辐射效率反映了结构表面法向振速均方相同时各种速度分布辐射声功率的能力[15]，因此可以用各个频段内结构表面的法向振动均方值和结构辐射效率来解释结构的辐射声功率变化，当弹性基础刚度为Kf=0N/m3、边界旋转刚度Kr=0N/rad时，不同边界支持刚度时加筋板表面振动速度均方值曲线和声辐射曲线见图7。随着边界支持刚度的增加，低频时加筋板振动均方速度减小（图7（a）），低频声辐射效率基本不变（图7（b）），所以低频辐射声功率有所减小（图7（c））；中高频的振动均方速度基本不变，声辐射效率明显增加，从而辐射声功率增大，结构总辐射声功率增加（图7（d）），这主要是因为当边界支持刚度较小时，加筋板结构可近似为自由板，其辐射效率很低[16]，当支持刚度增大时，声辐射效率会明显增加，而边界支持刚度对整个加筋板结构的振动幅值影响较小（图7（a）），即边界支持刚度增加时，声辐射效率的增加引起结构辐射声功率增加。所以在结构噪声控制时，应尽量控制边界支持刚度，“软”边界可以减小结构辐射效率。

2.3.2 边界旋转刚度的影响

当弹性基础刚度Kf=0N/m3、边界支持刚度Kt=1×1015Pa时，不同边界旋转刚度时加筋板表面振动速度均方值曲线和声辐射曲线见图8，在图中有个明显的特征：随着边界旋转刚度的增加，加筋板振动均方速度曲线与结构辐射声功率曲线有相同的变化趋势（图8（a）和图8（c）），这主要是因为边界旋转刚度对加筋板声辐射效率影响较小（图8（b）），此时对加筋板辐射声功率起主要作用的是结构表面的均方速度。随着边界旋转刚度的增加，加筋板固有频率会略增加，加筋板振动均方速度曲线略向高频移动（图8（a）），在恒定频带内（300 Hz）加筋板的声辐射功率见图8（d），从图中可以看出，边界旋转刚度对辐射总声功率影响不大。

2.3.3 弹性基础刚度的影响

不同弹性基础刚度、弹性刚度作用范围、弹性基础位置时四周刚性固定加筋板表面振动速度均方值曲线和声辐射曲线见图9－图11。

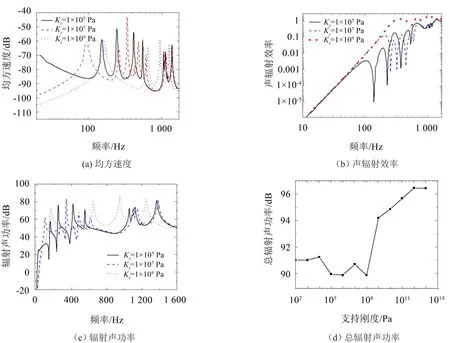
图7 不同边界支持刚度加筋板振动均方速度与声辐射

从图中可以看出不同弹性基础（刚度，范围或位置）时加筋板的辐射效率变化较小，即四周固定约束（或简支约束）的加筋板，如再施加额外的约束（如增加弹性基础刚度等），加筋板的辐射效率变化较小。加筋板结构表面振动速度均方值曲线与加筋板声功率曲线变化趋势基本相同，此时对加筋板辐射声功率起主要作用的是结构表面的振动速度均方值。

随着弹性基础刚度的增加，加筋板结构表面振动速度均方值曲线向高频移动（图9（a））。这是因为弹性基础的增加相当于增加了结构刚度，使结构的共振频率增加，特别是第1阶频率增加明显，在低频时加筋板表面均方速度被抑制，而中高频时加筋板表面均方速度基本不变，故低频时加筋板辐射声功率明显降低（图9（d）），如与弹性基础刚度Kf=0 N/m3时加筋板辐射声功率曲线相比，当Kf=2.5×105N/m3时，在 0～300 Hz、300 Hz～600 Hz频率段内辐射声功率分别下降了38.4%、44.5%，600 Hz～1 200 Hz频率段内辐射声功率基本相同，而在1 200 Hz以后频率段辐射声功率变化不大与弹性基础（Kf=5×109N/m3）范围等于加筋板面积时相比，当弹性基础范围减小一半时，此时加筋板共振频率明显减小且振动峰值增多（图10（a）），在低频时加筋板表面速度均方速度显著增加，这是由于加筋板的相当刚度减小，并且不对称的弹性基础约束激发出较多的共振模态，因此低频时加筋板辐射声功率明显增加（图10（c）），如在0～400 Hz、400 Hz～800 Hz频率段内辐射声功率分别增加了27.5%、46.9%。800 Hz以后频率段辐射声功率几乎没有变化（图10（d））。

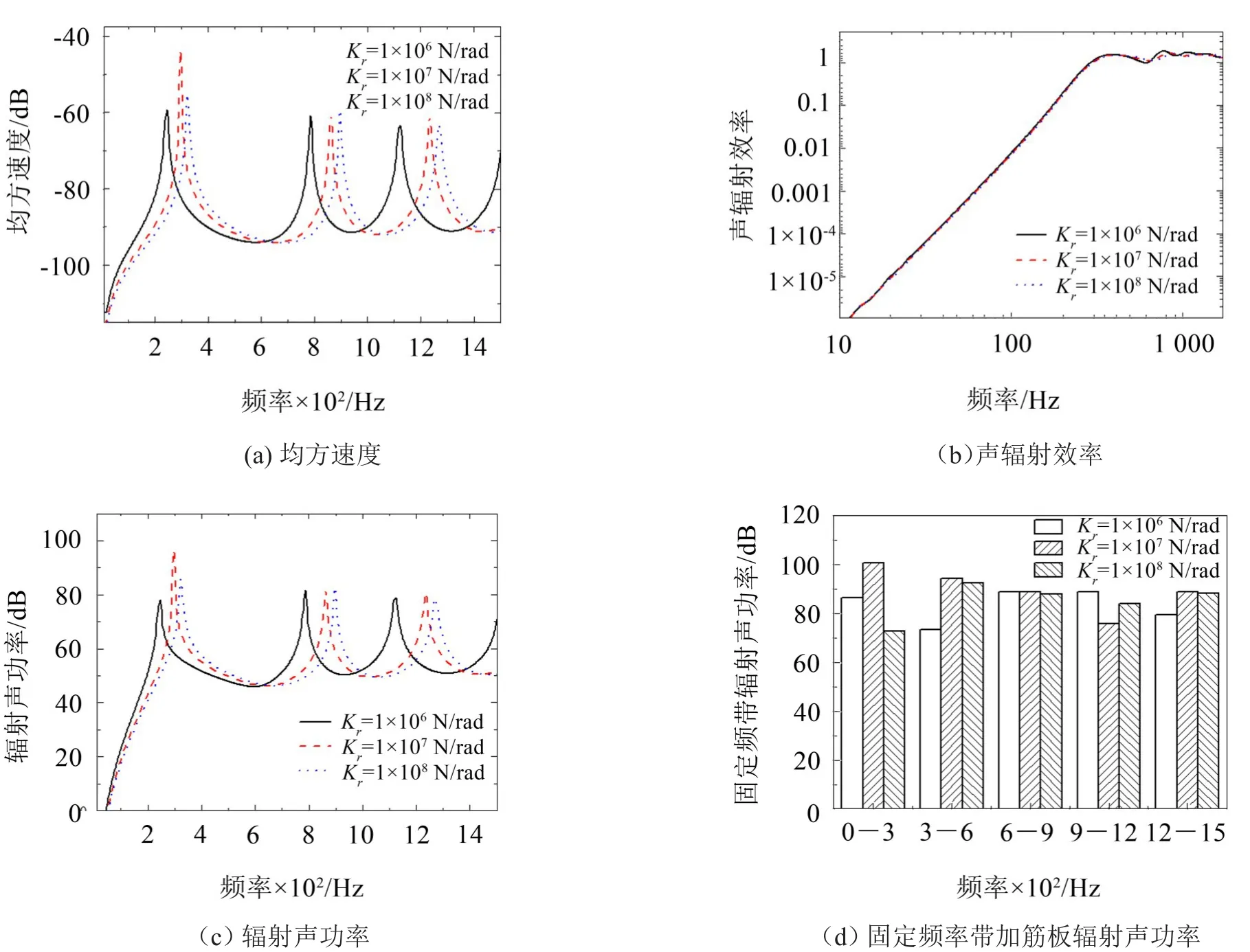
图8 不同边界旋转刚度加筋板振动均方速度与声辐射

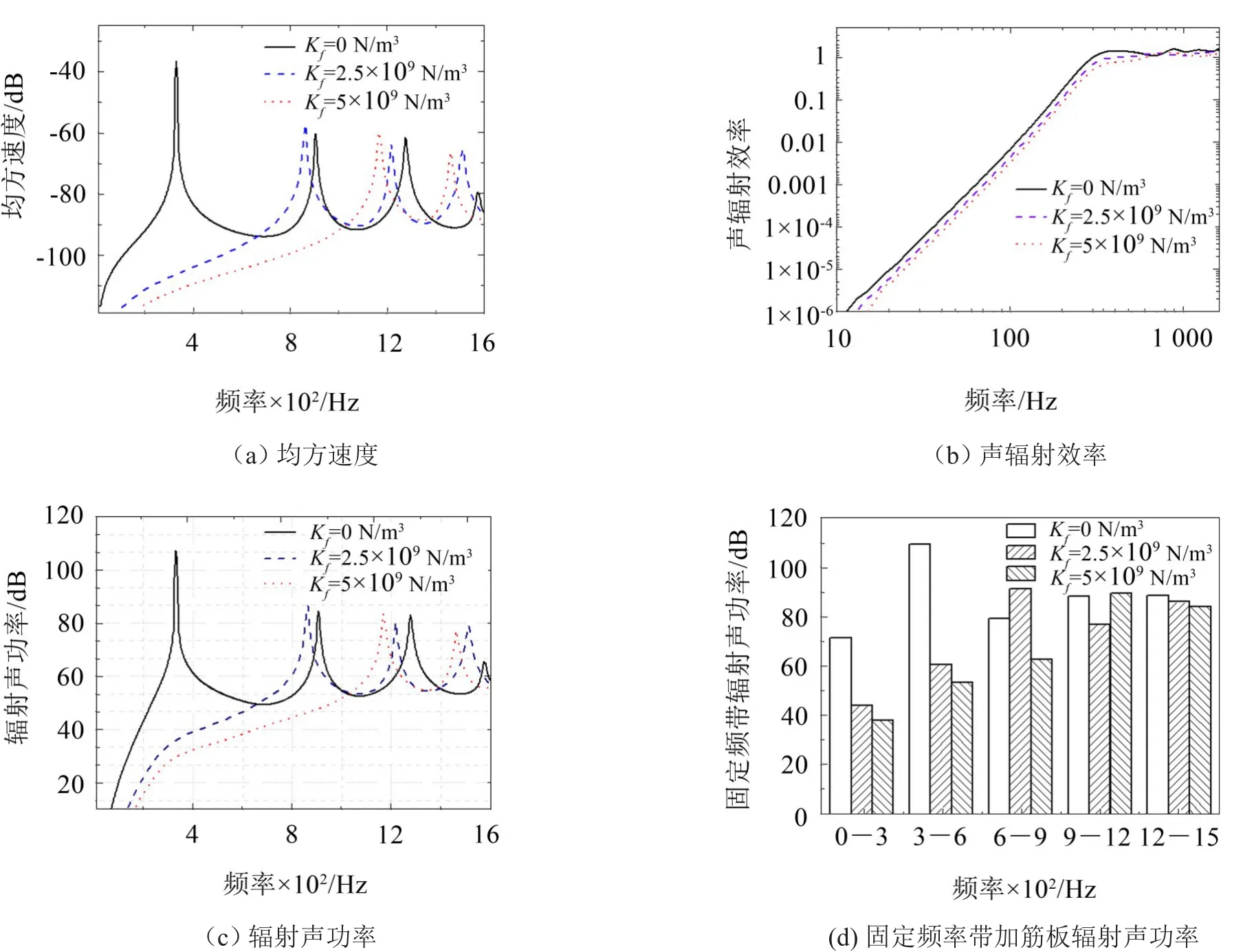
图9 不同弹性基础刚度加筋板振动均方速度与声辐射

弹性基础（Kf=5×109N/m3）分别位于y=b/4和y=b/2时（注：此时弹性基础范围仅为一条直线），在位置y=b/4时由于弹性基础约束的不对称，在低频时加筋板被激发出较多的共振模态（图11（a）），此时低频处加筋板振动峰值增多，加筋板被激发出较多的辐射声功率峰值，与局部弹性基础在y=b/2相比，在位置y=b/4时0～300 Hz，300 Hz～600 Hz、600 Hz～900 Hz频率段内加筋板辐射声功率分别增大了13.8%，4%，16%。900 Hz以后频率段辐射声功率几乎没有变化（图11（d））。

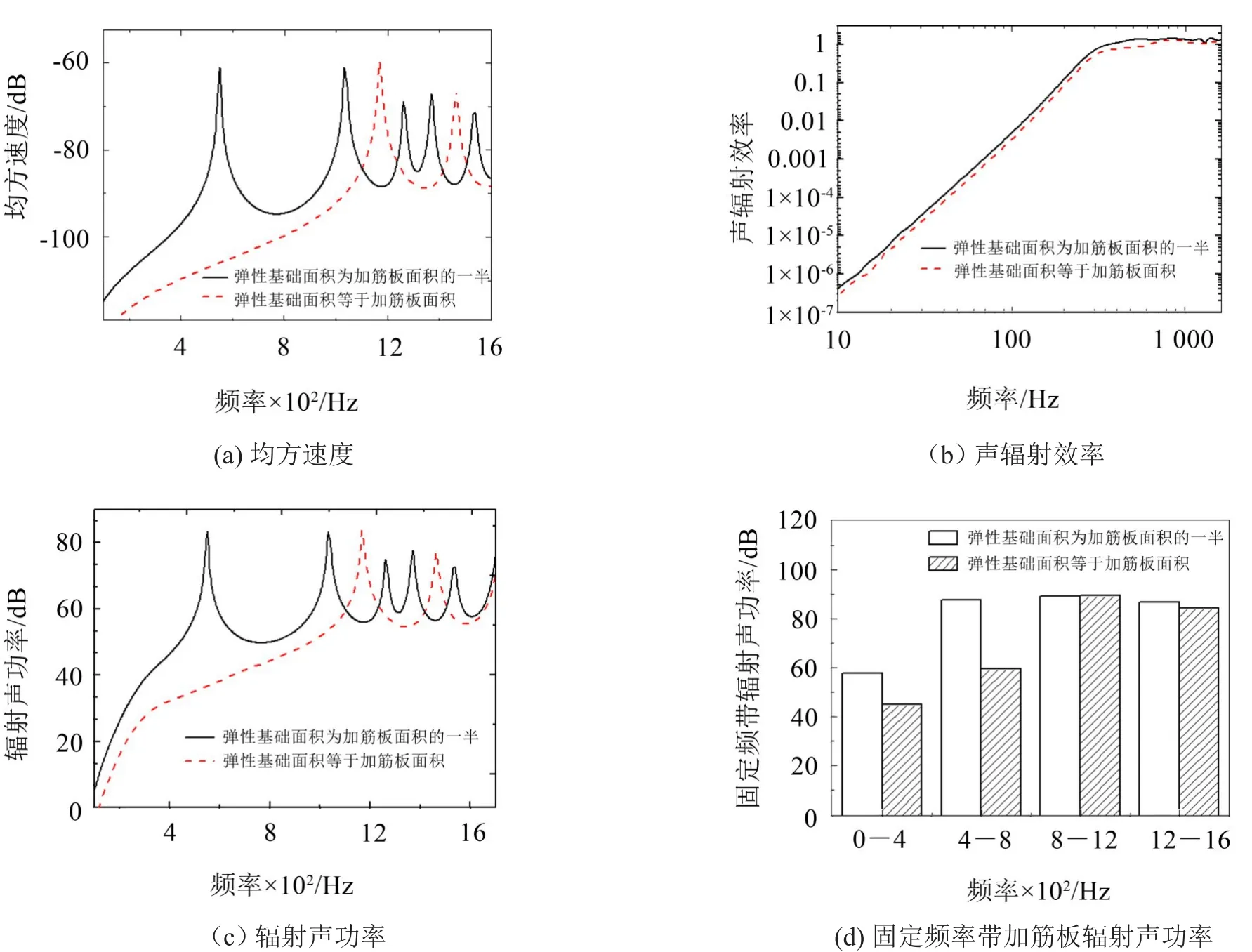
图10 不同弹性刚度作用范围加筋板加筋板振动均方速度与声辐射

3 结语

本文建立了弹性边界条件下弹性基础加筋板辐射声功率模型，研究了边界条件和弹性基础对加筋板振动特性和辐射声功率特性的影响，主要结论如下：

（1）从自由边界—简支边界—刚性固定边界过渡过程中，存在两个固有频率急剧增加的阶段，在实际结构振动计算时要特别注意，以免引起大的误差。另外边界支持刚度会引起振动模态的改变，而边界旋转刚度对振动模态的影响较小。

（2）边界支持刚度是影响结构辐射效率的重要参数，“软”边界有助于降低结构辐射效率。

（3）当支持边界足够大时，增加结构的边界旋转刚度，结构辐射声功率变化不大。

（4）当支持边界足够大时，增加弹性基础刚度时，加筋板的辐射效率变化较小，此时可以增加弹性基础的刚度以减小低频结构表面节点速度均方值，降低结构低频辐射噪声，同时弹性范围、弹性位置等可能影响辐射声功率减小的幅度。

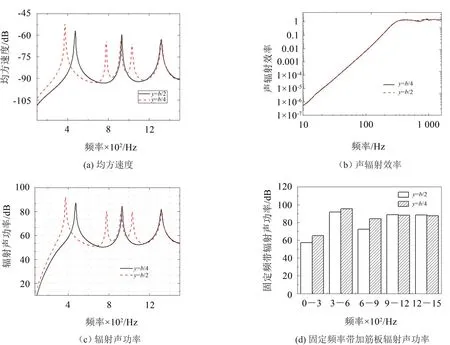
图11 不同弹性基础位置加筋板振动均方速度与声辐射