基于HLS-SVDR和SPPCS的CEEMD的滚动轴承微故障特征提取*
徐 波, 周凤星, 马娅婕, 严保康, 黎会鹏
(1.武汉科技大学信息科学与工程学院 武汉,430081) (2.黄冈师范学院电子信息学院 黄冈,438000)
引 言
Huang等[1]提出了Hilbert-Huang变换算法(Hilbert-Huang transform, 简称HHT),适合处理非平稳随机信号,在机械故障诊断中得到广泛应用。经验模态分解(empirical mode decomposition, 简称EMD)作为HHT的核心部分,算法直观简单,具有正交性、完备性和自适应性等特点,然而存在包络拟合过冲/欠冲、端点效应和模态混叠等问题,严重影响其推广和应用。针对模态混叠问题,胡爱军等[2]提出了加入高频谐波再进行EMD分解的模态混叠的消除方法。曹莹等[3]提出了基于形态滤波预处理与特征尺度匹配的模态混叠抑制方法。但上述方法经验性较强,缺乏自适应性。汤宝平等[4]提出了基于独立分量分析的模态混叠消除方法,但该方法没有考虑端点效应严重影响EDM分解结果的有效性。Yeh等[5]提出了互补集总经验模态分解方法,通过向原始信号中添加两对相反的白噪声信号分别进行EMD分解,克服了EEMD的白噪声残留的问题,有效消除了模态混叠问题,对端点效应也有一定的抑制作用,是目前消除模态混叠简单且有效的方法。
针对包络拟合过冲/欠冲问题,相关学者提出了如三次B样条插值[6]、分段三次Hermite样条插值[7]、分段抛物线插值[8]、单调分段三次样条插值法[9]和分段约束三次样条插值[10]等改进方法。上述方法中,三次B样条插值的拟合特性没有明显提高;分段三次Hermite样条插值的平滑性不好;单调分段三次样条插值法的计算量太大;分段约束三次样条插值的包裹性差。
针对端点效应问题,相关学者提出了如镜像延拓[11]、最大相关波形延拓[12]、极值波延拓[13]、最大斜率再优化极值延拓[14]、PDE信号修补[15]、均生函数周期叠加外推[16]、最小平方距离相关[17]及加窗函数[18]等基于信号特征或极值特征的延拓方法。但这些方法具有很强的经验性,泛化能力差。另外一些学者提出了如支持向量回归预测[19]、支持向量机[20]、神经网络延拓[21]及自回归综合滑动平均模型延拓[22]等基于数据预测延拓的方法,能够较为准确地进行端点延拓,然而算法复杂、效率低、参数难以选择,工程实现度低。
笔者在总结上述改进方法的基础上,提出同伦-最小二乘支持向量双回归的保形分段三次样条CEEMD方法,获得一个完备的CEEMD算法。通过对实际振动信号的分析及滚动轴承微故障频率特征的提取来验证该方法能够从整体上解决EMD存在的拟合过冲/欠冲、端点效应和模态混叠问题。
1 基本原理
1.1 CEEMD简介
在对信号x(t)做EEMD分解时,令集总平均的次数为N,对x(t)第j次添加白噪声uj(t)后得到
(1)
令x(t)减去uj(t),得到
(2)
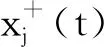
(3)
对式(3)求集总平均,获得
(4)
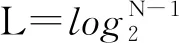
由于对x(t)分别添加同一白噪声,但符号相反,使得相加后残留在IMFj+和IMFj-中的白噪声基本互相抵消,从而使最后IMF分量中的白噪声基本互相抵消,上述添加符号相反的白噪声正是“互补”的本质。CEEMD不仅消除了模态混叠问题,而且基本上消除了白噪声残留问题。
1.2 包络拟合过冲/欠冲分析
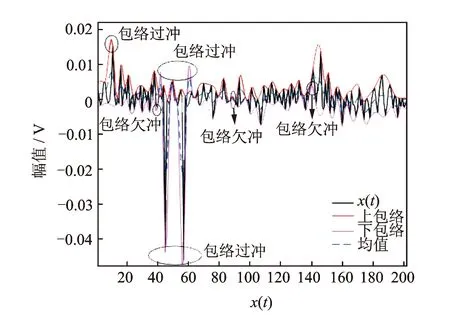
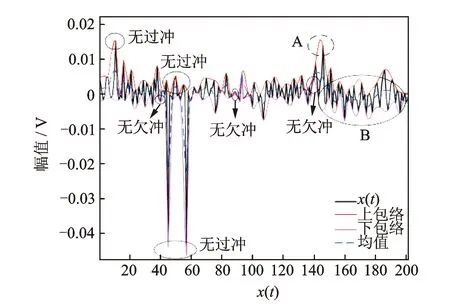
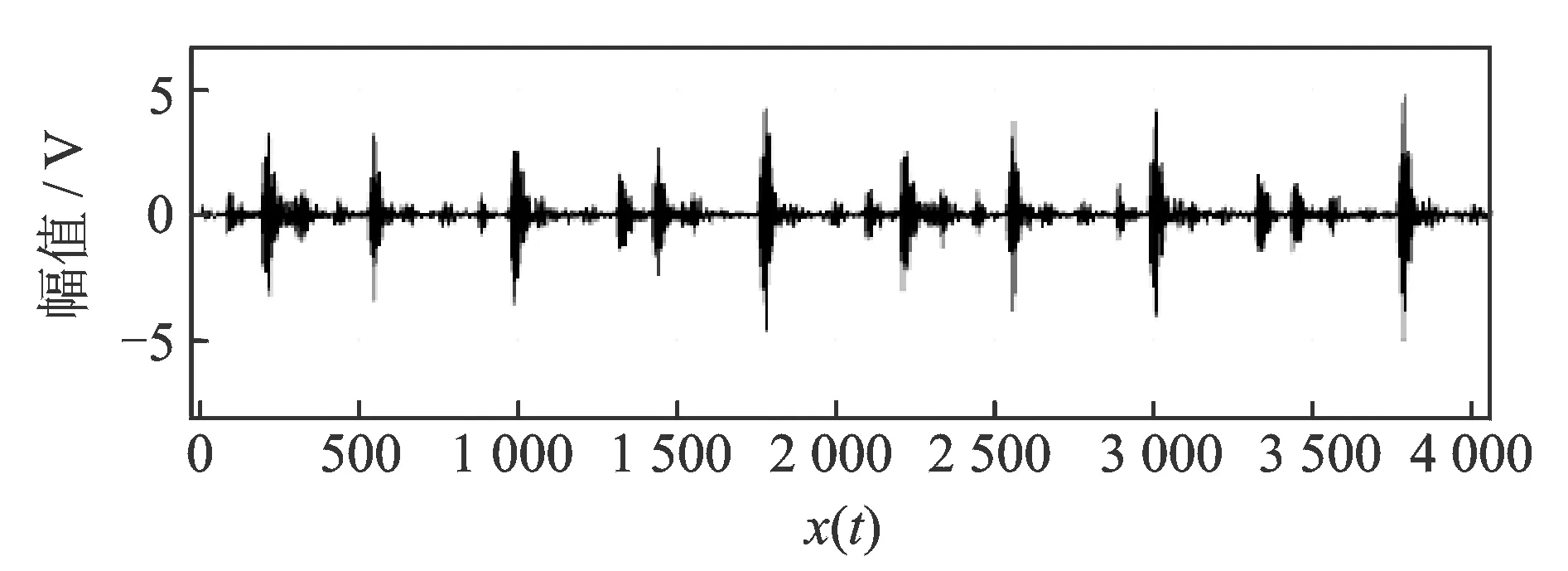
Huang在文章中没有给出构造上、下包络线时产生包络拟合过冲/欠冲问题的严格定义。龙思胜等[23]认为“拟合过冲/欠冲”现象是在待处理数据序列的每个子段内,所得拟合函数的部分数值大于这两个数据的大者或小于这两个数据的小者,并提出了一阶导数零点法,一定程度上解决了拟合过冲/欠冲问题。由于没有严格的数学依据及证明,而是根据处理数据时的经验,对于任意信号的有效性有待验证。使用最常用的三次样条插值对取自滚动轴承实验台的故障信号x(t)(如图1所示,其中x(t)为时间数据序列为无量纲单位)进行一次上、下包络线插值拟合,得到包络线如图2所示。
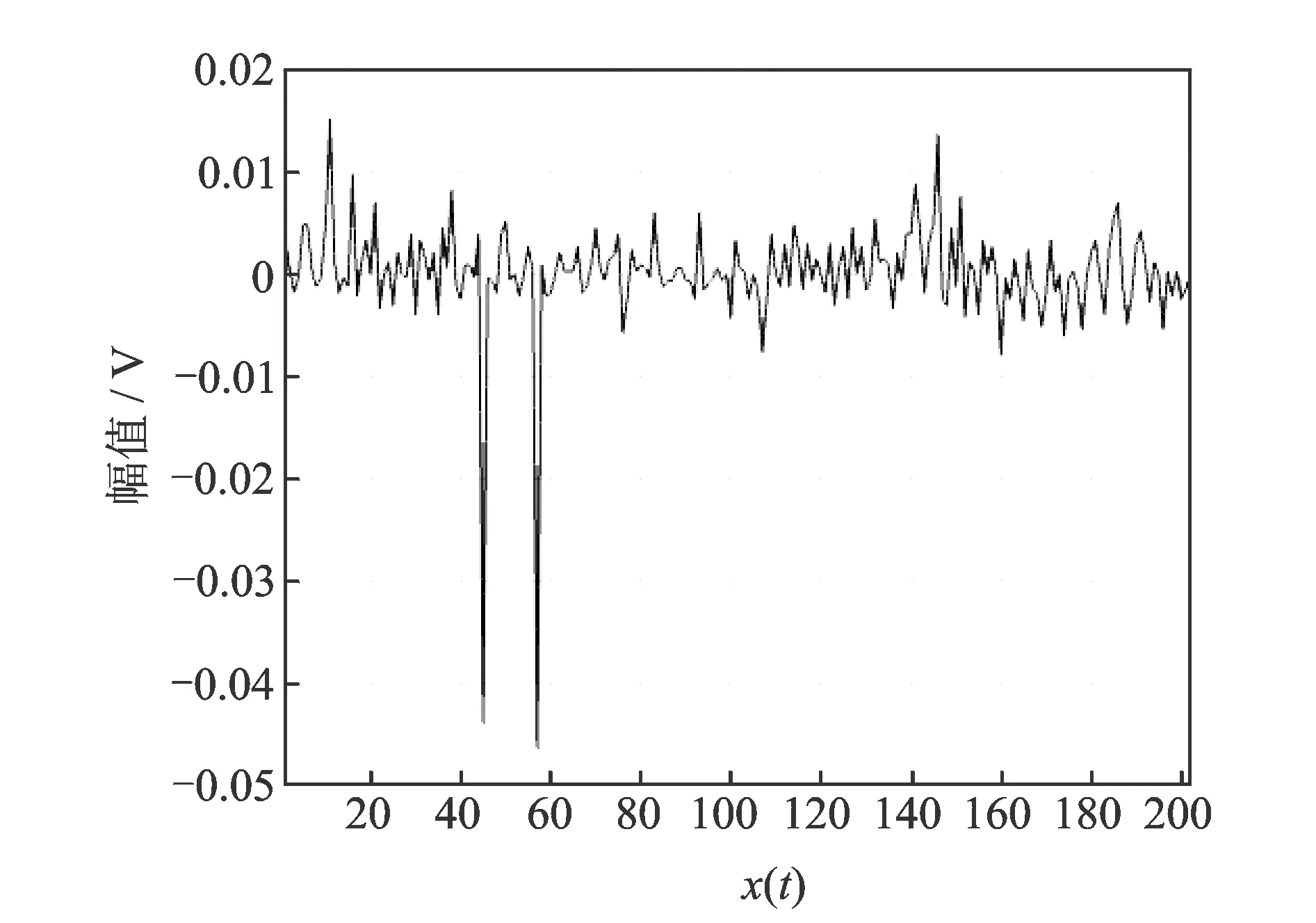
图1 滚动轴承振动信号x(t)Fig.1 Rolling bearing′s vibration signal x(t)
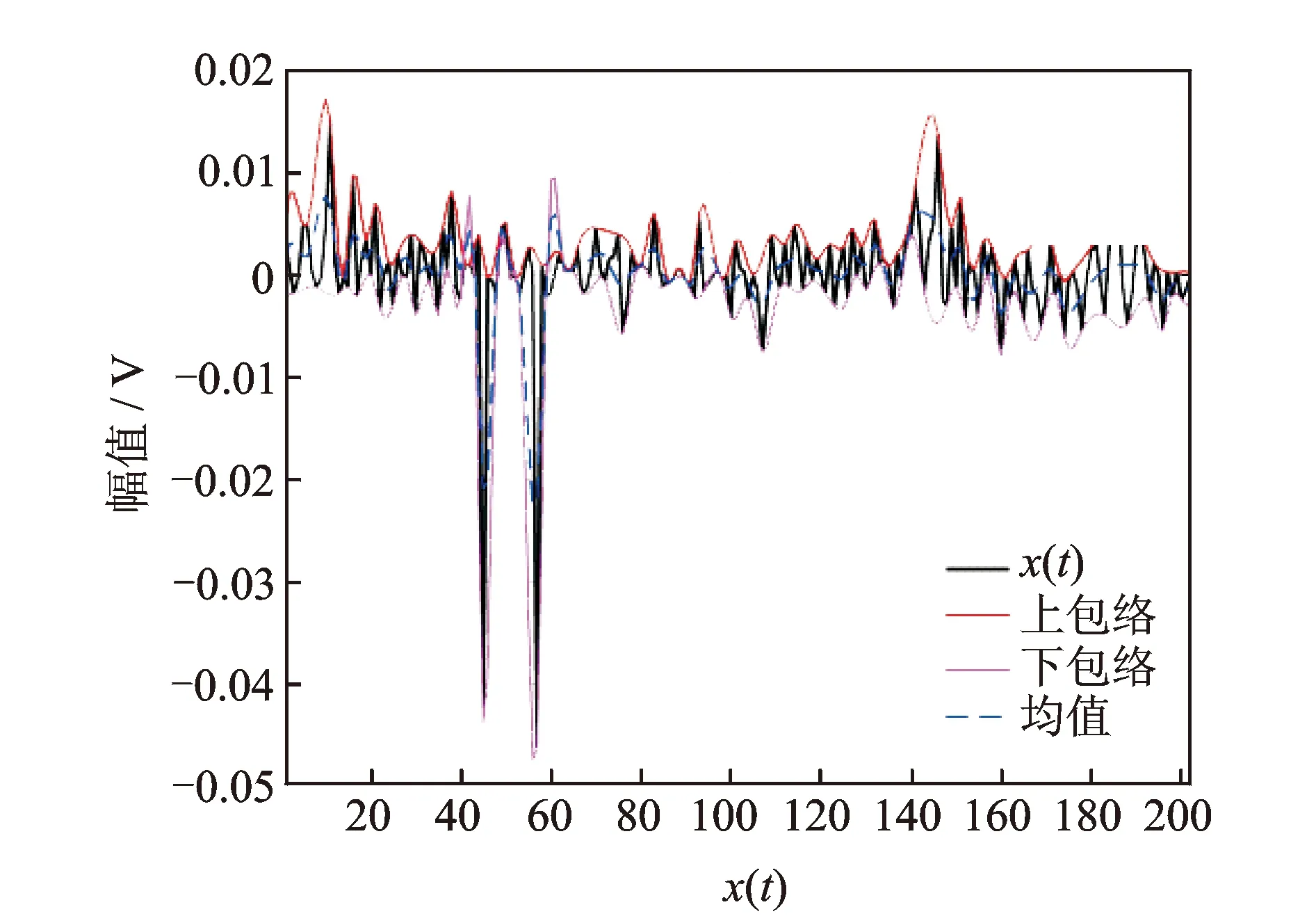
图2 三次样条插值的包络线Fig.2 The envelope curve of spline
为了便于观察,将图2中包络线进行局部放大,其放大图如图3,4所示,可以观测到包络线出现了明显的拟合过冲/欠冲问题。
1.3 端点效应分析
由于实际采集的信号的长度有限,信号的两端在极少数情况下能够获得有效的极值点,因此对极值数据序列进行插值拟合时,在上、下包络线在的两端出现发散现象,称为端点效应,且这种“发散”会随着分解过程地继续进行而不断向信号内部传播,最终“污染”整个信号而使分解结果严重失真而失去物理意义。采用图1中滚动轴承的振动信号x(t)进行端点效应的分析,并使用三次样条插值法对x(t)进行包络线拟合,结果如图5所示。由于信号x(t)两端不存在极值点,获得的上、下包络线在曲线两端出现严重的端点效应。

图3 三次样条插值的过冲问题的局部放大图Fig.3 The enlarged partial view of the overshoot problem of spline
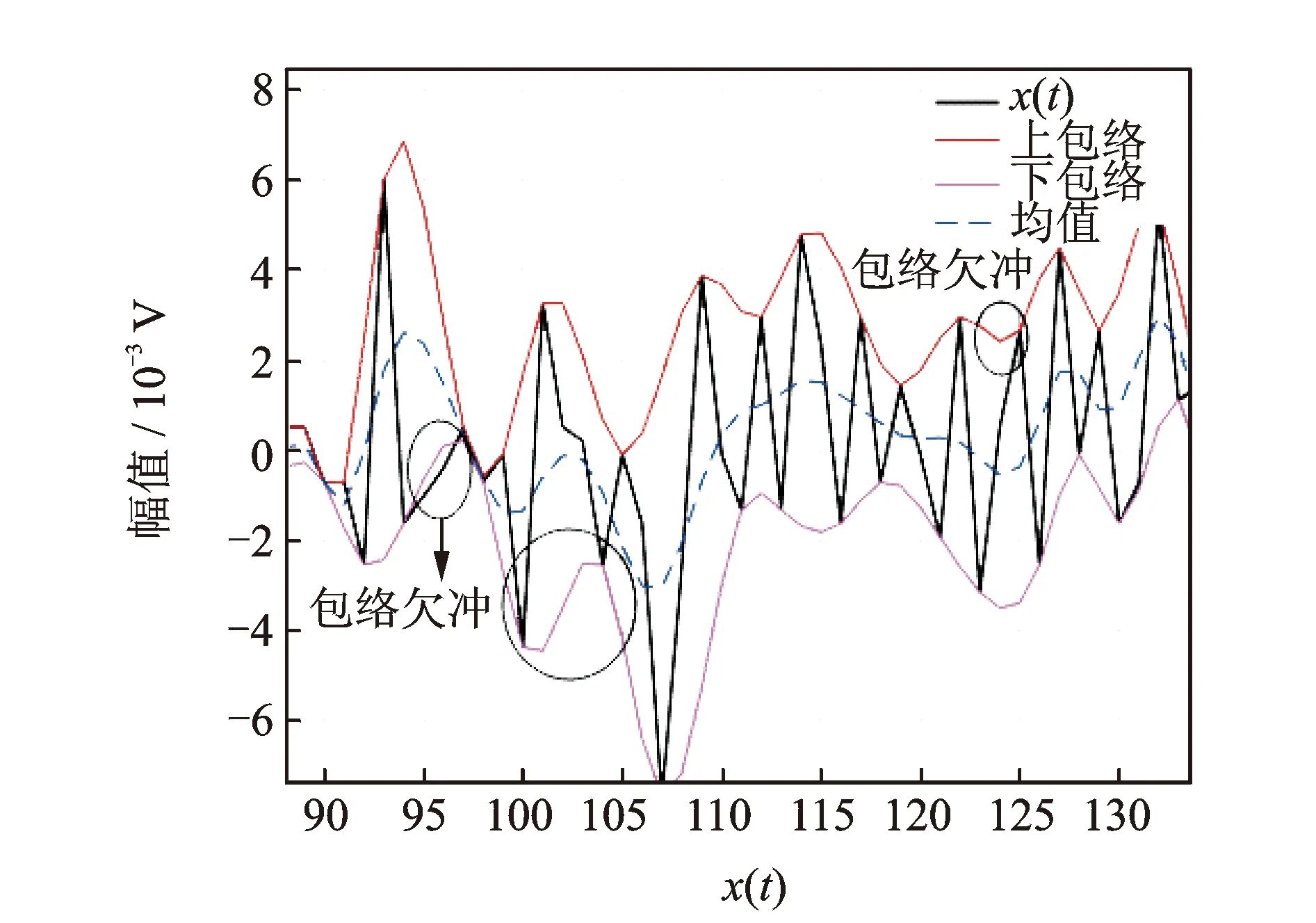
图4 三次样条插值欠冲问题的局部放大图Fig.4 The enlarged partial view of the undershoot problem of spline
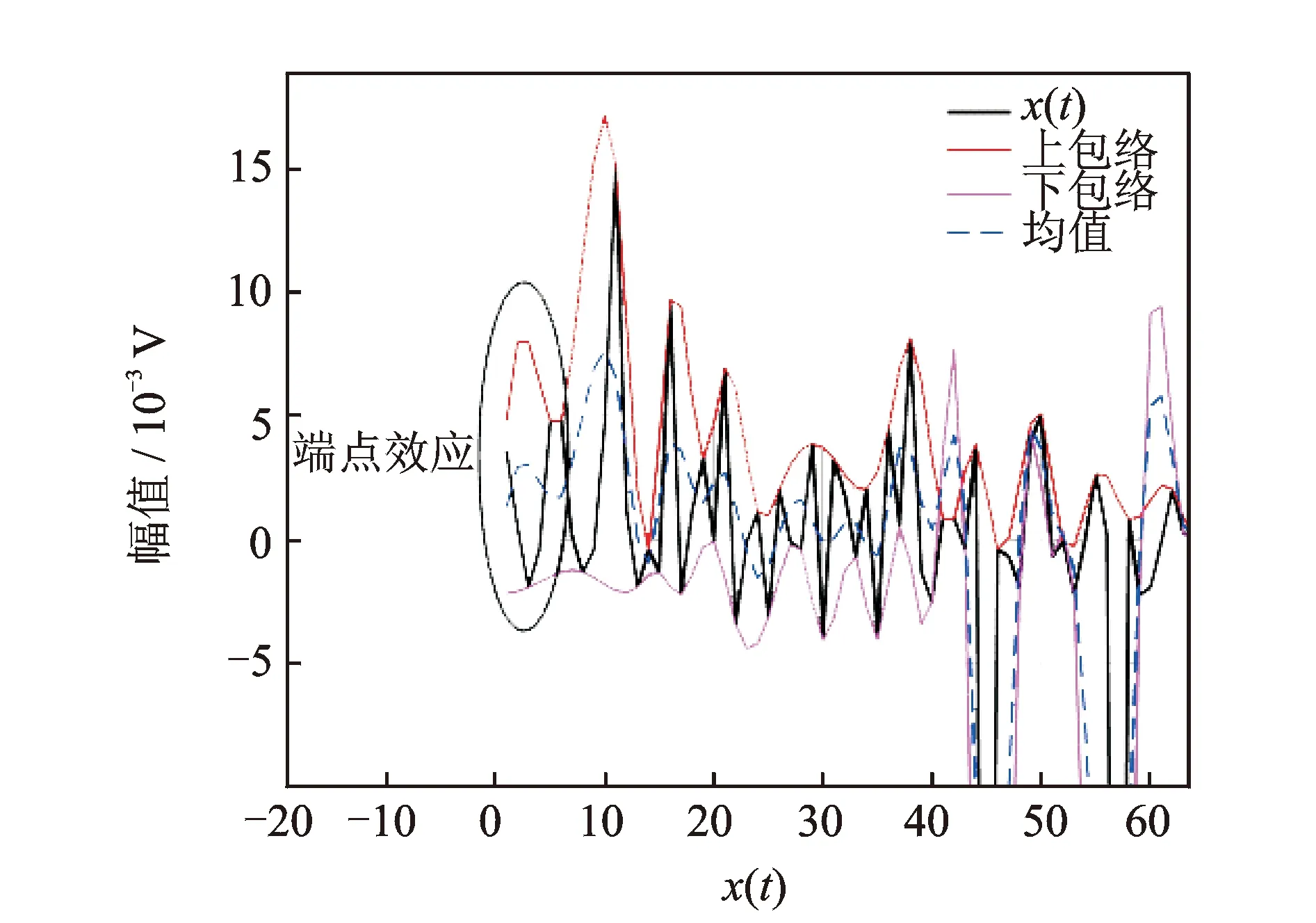
图5 三次样条插值端点效应的局部放大图Fig.5 The enlarged partial view of the left end effect of spline
2 保形分段三次样条插值算法
2.1 保形分段插值的构造
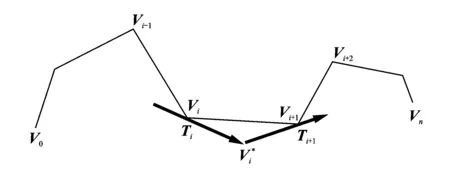
给定平面点集Ti(xi,yi)(i=1,2,…,n),将相邻两点使用直线依次连接成一个多边形{T0,T1,…,Tn},并令多边形的边向量为
Si=ti-ti-1(i=1,2,…,n)
(5)
如果ti×ti-1与ti×ti+1平行且方向相反,则Ti为{T0,T1,…,Tn}的拐点。
2.2 插值曲线在型值点处的切矢
由多边形的边矢定义可知,插值曲线在Ti处的切矢Ki定义为:如果Ti是多边形{T0,T1,…,Tn}的拐点,则令
Ki=kiSi+(1+ki)(-Si+1)
(6)
否则令
Ki=kiSi+(1-ki)(Si+1)
(7)
其中:Ki(0 如果Ti-1,Ti,Ti+1三点共线,则定义Ti-1=Ti=Ti+1=Si,即选取ti-1=0,ti+1=1。通过切矢的定义可知,KiKi+1总是平行KiSi且有相同方向,故分别过Ti和Ti+1且平行于Ki和Ki+1直线li和li+1的交点Vi为 (i=0,1,2,…,n-1) (8) 如果Vi-1,Vi,Vi+1,Vi+2构成的三边形是凸的,则令控制多边形{v-1v0…vnvn+1}的边矢量为 ai=Vi-Vi-1(i=0,1,…,n+1) (9) 给定m+1个控制顶点ri(i=1,2,…,m),相应的三次样条曲线的分段函数表示为 (0≤u≤1;k=0,1,2,…,m-3) (10) 其中:基函数为 (11) 从基函数可以得到端点的性质 (12) 则三次样条曲线的deBoor点定义为 (13) 由式(9)及式(13)可得 a0=(a1-a2)/4 (14) a0a1=a1a2/4 (15) Vi-1,Vi,Vi+1,Vi+2构成的三边形是凸的,可保证插值曲线在两端不会出现多余的拐点,并设定λi的取值范围,使得三次样条插值曲线保形。如果aiai+1,ai+1ai+2方向一致,则Vi-1,Vi,Vi+1,Vi+2构成的三边形是凸的,所得交点为 (16) 如果aiai+1,ai+1ai+2方向相反时,则Vi-1,Vi,Vi+1,Vi+2构成另一个拐向,记为 (17) 令 (i=0,1,…,n) (18) 根据图6所示的控制多边形,如果选取 0<λi≤ei(i=0,1,…,n) (19) 则通过调节参数λi满足式(19),构造出保形分段三次样条插值法。 图6 控制多边形Fig.6 Controlled polygon 为了验证笔者提出的SPPS插值方法能够有效地消除包络拟合过冲/欠冲问题,使用图1中的振动信号x(t)进行实验分析,结果如图7~9所示。使用改进的三次B-样条插值法进行包络线插值拟合,拟合结果如图7所示。对比图7与图2的拟合结果可知,改进的三次B-样条插值得到的上、下包络曲线依然出现严重的拟合过冲/欠冲,并没有消除拟合过冲/欠冲问题。 为了进一步对比其他插值方法,采用分段约束三次样条插值方法进行包络线拟合,拟合结果如图8所示。对比图8与图7的拟合结果可以看到,采用分段约束三次样条插值方法拟合的上、下包络曲线没有出现拟合过冲/欠冲现象,但从图中A,B两处拟合的曲线段可以观察到曲线拟合过陡,曲线不够平滑,使得拟合曲线的有效性不能得到保证,限于篇幅,此处不对上述其他插值方法进行对比分析。 针对图8中的拟合曲线出现不够平滑的问题,笔者提出了保形分段三次样条插值法拟合包络曲线,拟合结果如图9所示。拟合结果表明,该方法不但能够有效抑制拟合过冲/欠冲问题,而且拟合的包络曲线与图8相比,更平滑、有效,为后续的CEEMD分解过程奠定了基础。 图7 三次B-样条插值的包络线Fig.7 The envelope of B-spline 图8 分段约束三次样条插值的包络线Fig.8 The envelope of constrained piecewise spline 图9 保形分段三次样条插值的包络线Fig.9 The envelope of shape-preserving piecewise spline 支持向量回归(support vector machine regression,简称SVR)算法具有十分出色的预测能力。Suykens等[24]提出了最小二乘支持向量回归(least squares support vector regression,简称LS-SVR)算法,提高了SVR的求解效率,降低了SVR的学习难度。另外,在实际的工程应用中,许多的研究对象是具有多输入多输出的复杂系统。包络均值曲线左、右预测覆盖方法是一个两输入两输出的非线性系统。因此,针对多输入多输出,提出了同伦-最小二乘支持向量双回归(HLS-SVDR)算法,算法如下。 设已知训练集X={(x1,y1),…,(xk,yk)},其中xk∈Rd,yk∈Rm,即有d维输入,m维输出。假设有l个训练样本,即k=1,2,…,l。令yk,m表示yk中第m维输出的值(m=1,2,…,N)。模型的目标函数和约束条件为 (m=1,2,…,n;k=1,2,…,l) (20) 其中:ηk为第K个输入变量所对应的所有维数输出的拟合误差和;ξk,m为第K个输入变量所对应的第m维输出的拟合误差;C0为所有维输出拟合误差的惩罚系数;Cm为第m维输出拟合误差的惩罚系数。 其Lagrange函数形式为 (21) 引入同伦算法,即对于两个函数f(x)和g(x)引入一个嵌入变量λ,构造一个新的函数φ(x,λ)=(1-λ)f(x)+λg(x),其中,参数λ∈(0,1)。由于具有良好的收敛性,能够有效地求解非线性代数方程组,在科学和工程中得到广泛应用[25]。 在多输出最小二乘支持向量回归算法中,引入同伦嵌入变量λ可以将惩罚参数区间(0,∞)转化为有限区间(0,1),大大缩短惩罚参数的优化时间。以此构造HLS-SVDR算法,目标函数和约束条件为 (λm∈(0,1);m=1,2;k=1,2,…,l) (22) 其Lagrange函数形式为 (23) 分别对ωm,bm,ξk,m,ηk,βk和αk,m求偏导并令其为零,可得 (24) 根据式(24),消除ωm,bm,ξk,m和ηk,可得Lagrange乘子式αm=(α1,m,α2,m,…,αl,m)T,β=(β1,β2,…,βl)T和偏置bm的求取方程,即 其中:K(·,·)为第m维输出的核函数。 令Km=(Km(xk,xk′))l×l,E=(1,1,…,1)T∈Rl,ym=(y1,m,y2,m,…,yl,m)T,I为l×l的单位矩阵,则有 (26) 求解上式,得到同伦-多输出最小二乘支持向量回归第m维输出的函数形式为 (27) 图10 向量转换为张量Fig.10 Converting the vector to tensor 依据一维向量转为二阶张量的方法,将训练集X重构为两输入两输出的训练集X′ (xi∈Rd-1;l=i×d) (28) 将重构的训练集X′和X″分别作为同伦-最小二乘支持向量双回归算法的训练样本集和测试样本集。此外,核函数的选择也决定了训练模型的精确度,这里将使用最常用Gauss径向基核 Km(xk,xk′)=exp(-‖xk-xk′‖2/2σ2) (29) 由于σ∈(0,∞),难以优化。在此,同样采用同伦算法,对核函数进行改进 K1(xk,xk′)=exp(-‖xk-xk′‖2/2h2) K2(xk,xk′)=exp(-‖xk-xk′‖2/2(1-h)2) (30) 其中:h∈(0,1),使核参数h的优化时间大大缩短,同时也提高了最优核参数值的选择精度。 将同伦-最小二乘支持向量双回归与最小二乘支持向量双回归对振动信号CEEMD分解的包络均值m1(t)做实验对比。使用张量方法,将m1(t)数据序列重构为X′和X″。使用量子遗传(QGA)算法对最小支持向量双回归的惩罚参数C0,Cm及核参数σ及同伦-最小支持向量双回归的惩罚参数C0,λm及核参数h进行最优选择。实验结果如图11,12和表1所示。表1是对图11中的HLSSVDR算法和图12中LSSVDR算法在训练和测试精度、运行时间进行的对比分析。根据实验结果可知,基于HLSSVDR算法在预测精度及运算时间上都优于LSSVDR算法。 表1LSSVDR和HLSSVDR运行时间及预测误差 Tab.1TheelapsedtimeandpredictionerrorofLSSVDRandHLSSVDR 预测方法位置样本均方误差运行时间/sLSSVDR左端点右端点训练集8.814 9×10-70.012 0测试集1.220 3×10-60.011 7训练集1.240 9×10-60.011 4测试集1.279 7×10-60.012 2HLSSVDR左端点右端点训练集1.241 3×10-80.004 21测试集4.731 1×10-70.003 37训练集8.721 4×10-70.003 07测试集2.641 2×10-70.003 51 图11 LSSVDR左、右双向预测结果及误差结果Fig.11 The left and right prediction and error results by LSSVDR 为了进一步验证HLSSVDR在抑制端点效应方面的有效性,使用该方法对图1中x(t)两端的包络均值进行预测覆盖,实验结果如图13所示。图13(a)使用HLSSVDR方法对信号两端的包络均值进行预测,获得预测值,为了便于观察两端点的包络均值预测值,将图13(a)中的左、右端点的包络均值预测值进行局部放大,如图13(b)和图13(c)所示。其中,图13(b)中的A-B和图13(c)中的D-E是存在的极值点插值获得包络均值曲线段和包络均值预测曲线段。可以看到,左、右两端的包络均值预测值与真实值误差很小,预测精度高。另外,图13(b)中的B-C和图13(c)中的E-F分别对应的是不存在极值点的包络均值曲线段和包络均值预测曲线段,将其与没有进行端点效应处理的包络均值曲线进行对比,从图13(b)和图13(c)中可看到存在很大的误差。鉴于文中已经验证HLSSVDR方法有较高的预测精度,能够有效保证预测信号的准确度,因此EMD过程中保证有效的端点值才能保证信号分解的有效性。 图12 HLSSVDR左、右双向预测结果及误差结果Fig.12 The left and right prediction and error results by HLSSVDR 图13 包络线均值的预测Fig.13 The mean prediction values of the envelope 滚动轴承作为旋转机械设备的关键组件,易发生轴承内/外圈裂纹或断裂、滚动体磨损或破损等故障,对其进行早期检测与诊断,能够有效阻止故障发生,然而早期的故障特征频率极其微弱和难以提取。笔者提出了完备CEEMD方法用于滚动轴承微故障特征提取。 图14 滚动轴承故障实验与采集装置Fig.14 The fault testing and collecting device of rolling bearing 如图14所示,笔者选用美国凯斯西储大学滚动轴承故障实验台、驱动端轴承型号为SKF6205的轴承外圈故障的振动信号作为分析对象。轴承外圈故障采用电火花加工单点损伤,直径为0.173 4 mm(模拟轴承外圈微故障),采样频率为12 kHz,采样点数为4 096,电机转速为1 797 r/min,轴承外圈故障频率理论计算值为3.594 8×1 797/60=107.364 Hz。按照以上参数采集相关振动信号,如图15所示。 图15 滚动轴承外圈微故障振动信号Fig.15 The outer fault vibration signal of rolling bearing 为了进一步验证完备CEEMD方法的有效性和优越性,将其与传统的EEMD,CEEMD方法进行对比分析。首先,使用多小波包对原始振动信号进行降噪预处理,提高信号的信噪比。如图16所示。 图16 基于DDWP降噪后的振动信号Fig.16 Denoising vibration signal by DDWP 然后,分别利用EEMD,CEEMD及完备的CEEMD方法对降噪后的滚动轴承外圈微故障振动信号进行分解,获得IMF分量和残余量。实验结果如图17~19所示。经过CEEMD、完备CEEMD方法分解得到的IMF分量的个数少于EEMD方法获得的IMF分量个数。另外,CEEMD与完备CEEMD的IMF分量的个数相同,对比图17中的IMF分量C7,C9,C10,C11与图18,图19中的IMF分量C7,C8,C9,C10,可以观察到完备的CEEMD相应的IMF分量两端的端点效应,相对于传统的EEMD和CEEMD方法得到了抑制。 图17 EEMD分解的IMF分量Fig.17 The IMF component by EEMD 图18 CEEMD分解的IMF分量Fig.18 The IMF component by CEEMD 图19 完备CEEMD分解的IMF分量Fig.19 The IMF component by Complete CEEMD 为了准确说明完备CEEMD算法获得的IMF分量的特征信息,将分别对3种不同方法获得的IMF分量进行Hilbert变换,获得对应的滚动轴承外圈微故障振动信号的Hilbert边际谱如图20~22所示,分别为EEMD,CEEMD、完备CEEMD方法对应的滚动轴承外圈微故障振动信号的Hilbert边际谱。图20表明滚动轴承外圈微故障的特征频率107.3Hz及相应的倍频分量基本上被其他无关的特征频率所淹没,无法区分故障特征频率与无关特征频率。从图21可观察到表征滚动轴承外圈微故障的特征频率为107.3 Hz,但相应的二倍频特征频率不能很好地辨析。从图22中也可清晰地观察到表征滚动轴承外圈微故障的特征频率(107.3 Hz)及相应的二倍频、三倍频特征频率。 图20 EEMD分解的Hilbert边际谱Fig.20 The Hilbert Marginal Spectrum by EEMD 图21 CEEMD分解的Hilbert边际谱Fig.21 The Hilbert Marginal Spectrum by CEEMD 图22 完备CEEMD分解的Hilbert边际谱Fig.22 The Hilbert Marginal Spectrum by Complete CEEMD 上述实验分析表明,笔者提出的同伦-最小二乘支持向量双回归的保形分段三次样条CEEMD的改进方法能够更有效地提取滚动轴承外圈微故障的故障特征,能够整体上有效解决EMD的包络拟合过冲/欠冲、端点效应及模态混叠问题。 1) 通过对EEMD的包络拟合过冲/欠冲、端点效应、模态混叠问题进行分析。在CEEMD方法的基础上提出了同伦-最小二乘支持向量双回归的保形分段三次样条的CEEMD方法。实验结果表明,笔者所提方法能够更有效解决EMD存在的3个主要问题。 2) 针对包络拟合过冲/欠冲问题,提出了保形分段三次样条插值的EMD改进方法,该方法利用保形分段法来构造具有二阶逼近精度、分段少、运算量小的三次样条插值方法来抑制包络拟合过冲/欠冲问题,避免传统插值方法导致的插值误差随着分解过程的持续进行而出现误差不断累积,造成严重误差。实验结果表明,与其他插值法相比,笔者提出的插值方法能更有效地解决该问题。 3) 针对端点效应问题,提出了基于数据驱动的同伦-最小二乘支持向量双回归的包络均值预测覆盖的方法。同其他延拓方法相比,该方法不依赖信号本身特性,而是采用机器学习的方法对信号两端的包络均值进行预测,将预测值覆盖原有的随机插值。实验结果表明,该方法有较高的预测精度,收敛速度快、运算时间短,有效克服了基于数据预测抑制端点效应方法难以工程实现的问题。 4) CEEMD方法能够很好地解决模态混叠问题,但也存在对原始信号添加的正、负白噪声分解出的IMF+和IMF-分量个数不一定相等、导致少量模态混叠的问题。2.3 三次样条插值的保形性
2.4 实验验证

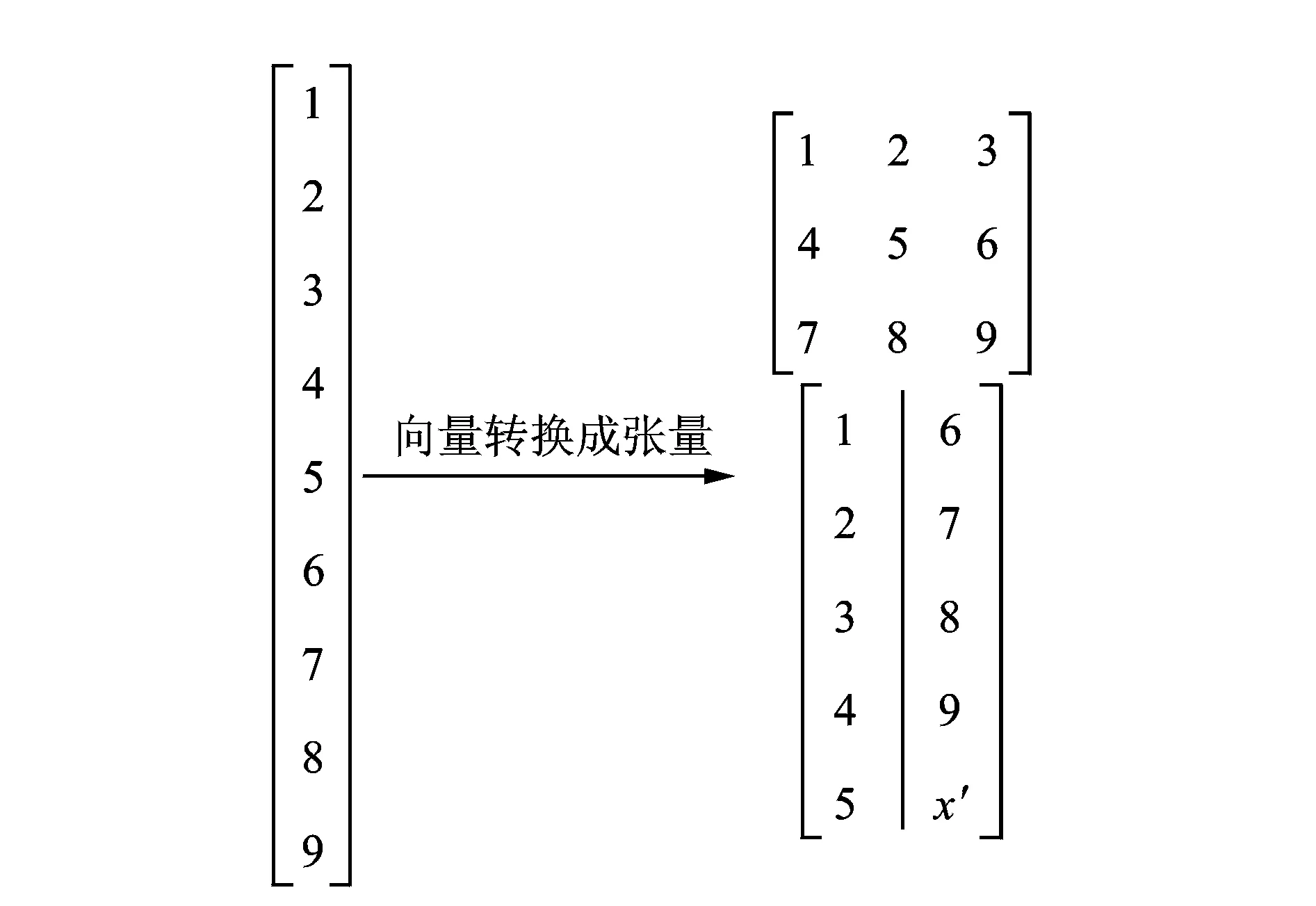
3 同伦-最小二乘支持向量双回归算法

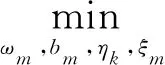

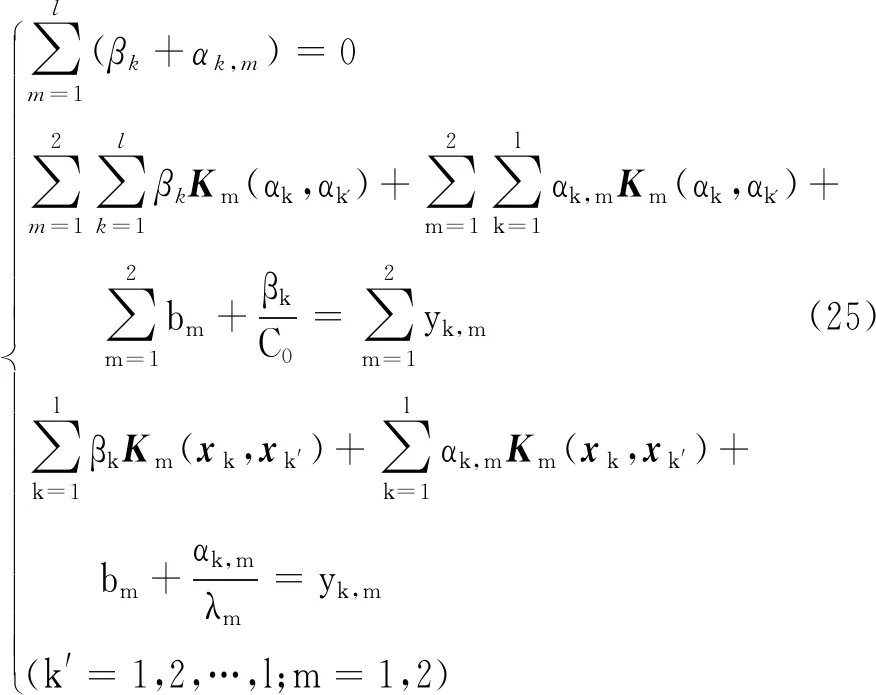

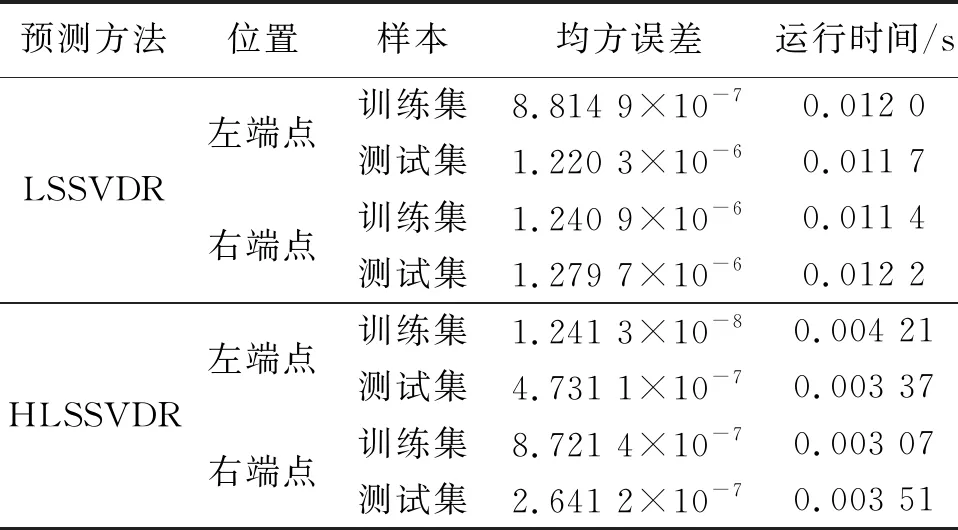
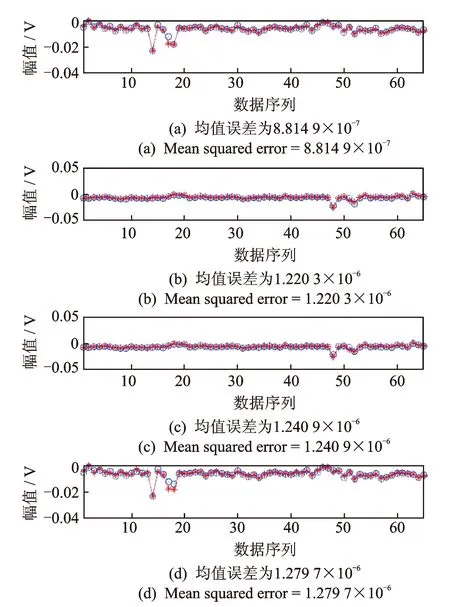
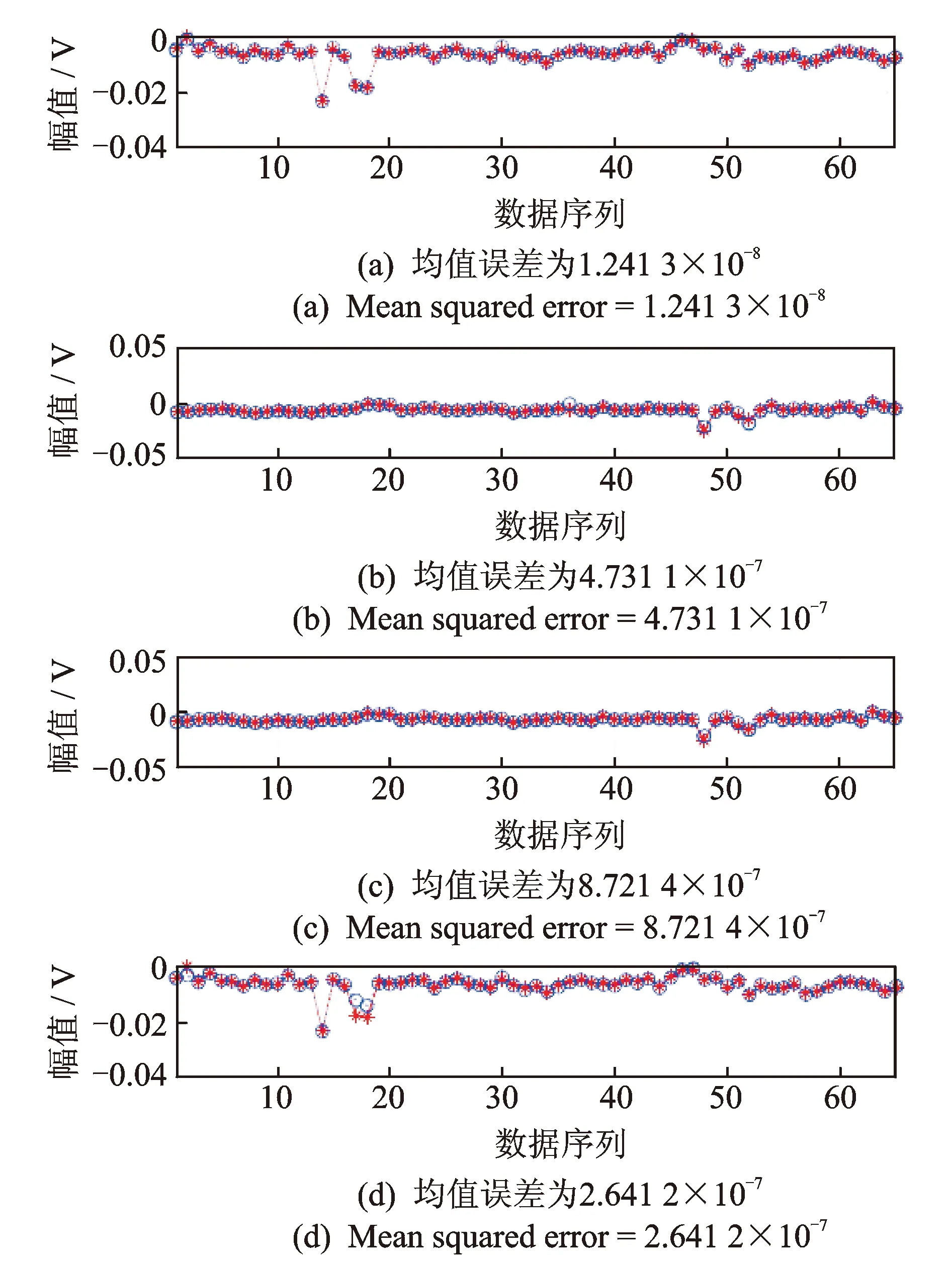
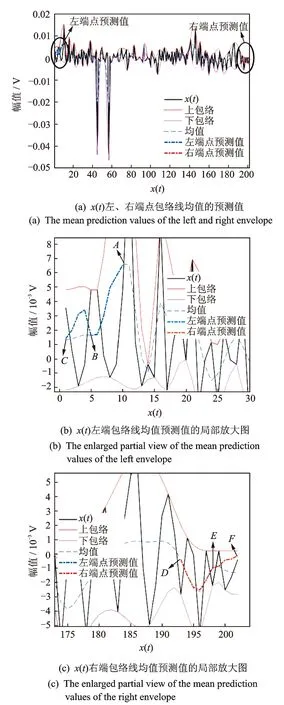
4 滚动轴承外圈微故障实例分析

4.1 滚动轴承实验台简介
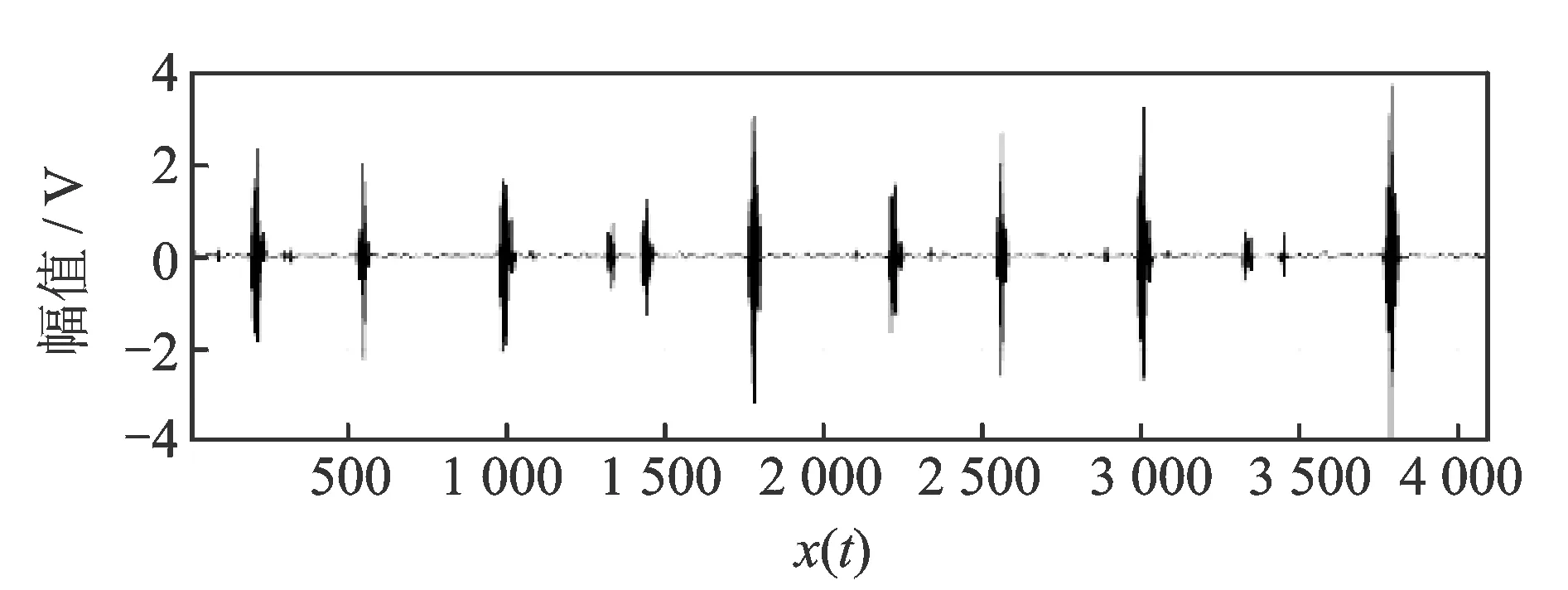
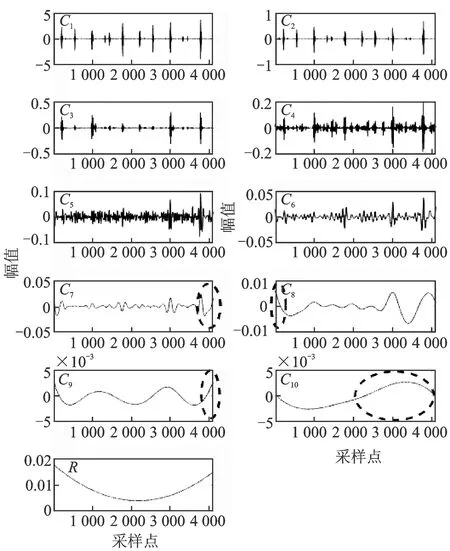
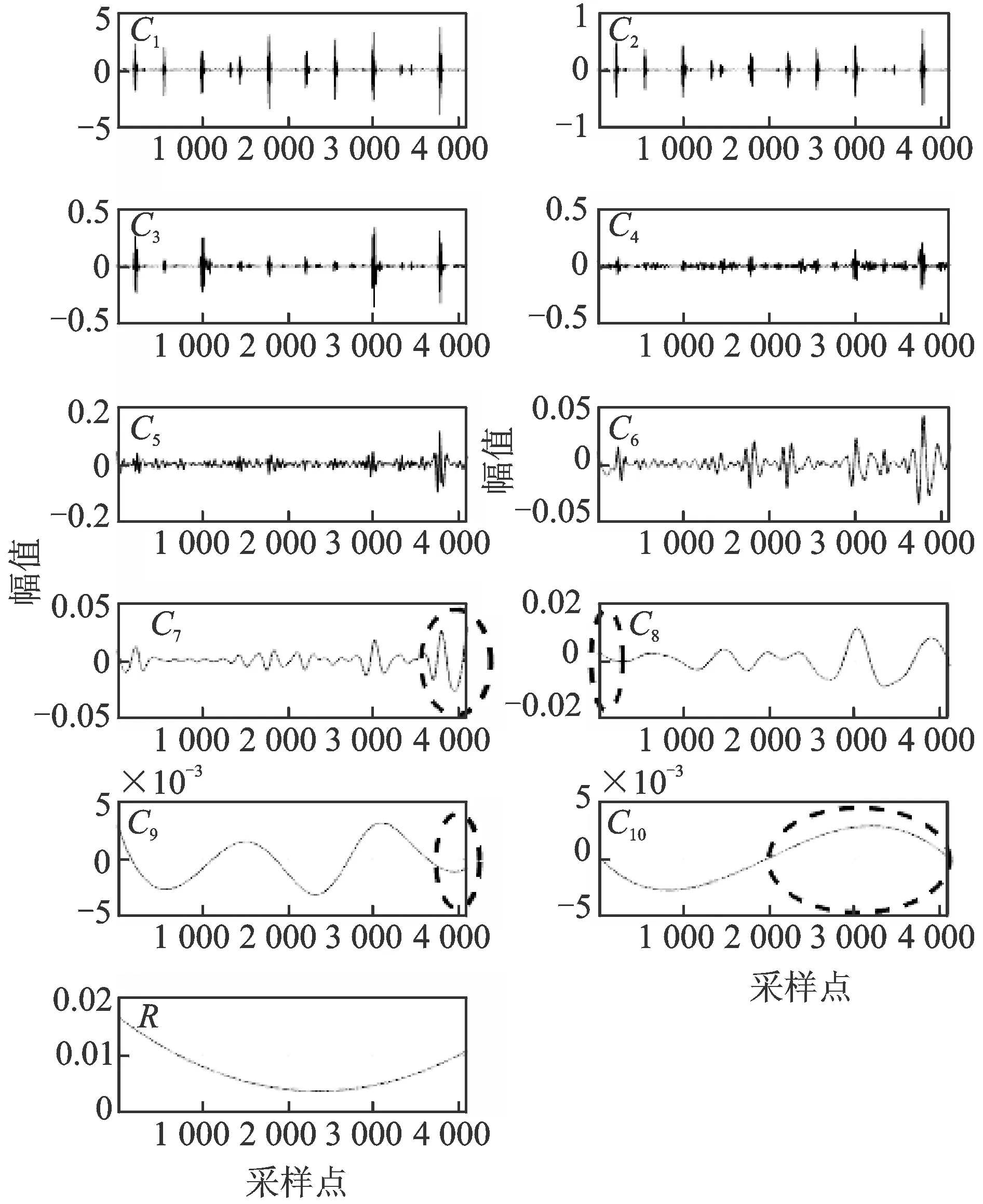
4.2 微故障特征提取

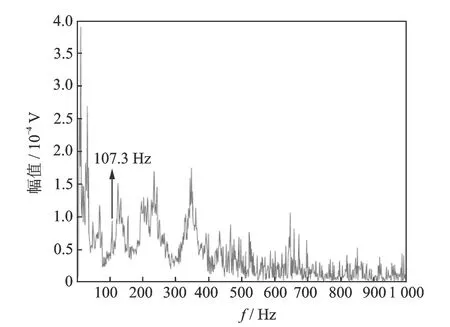
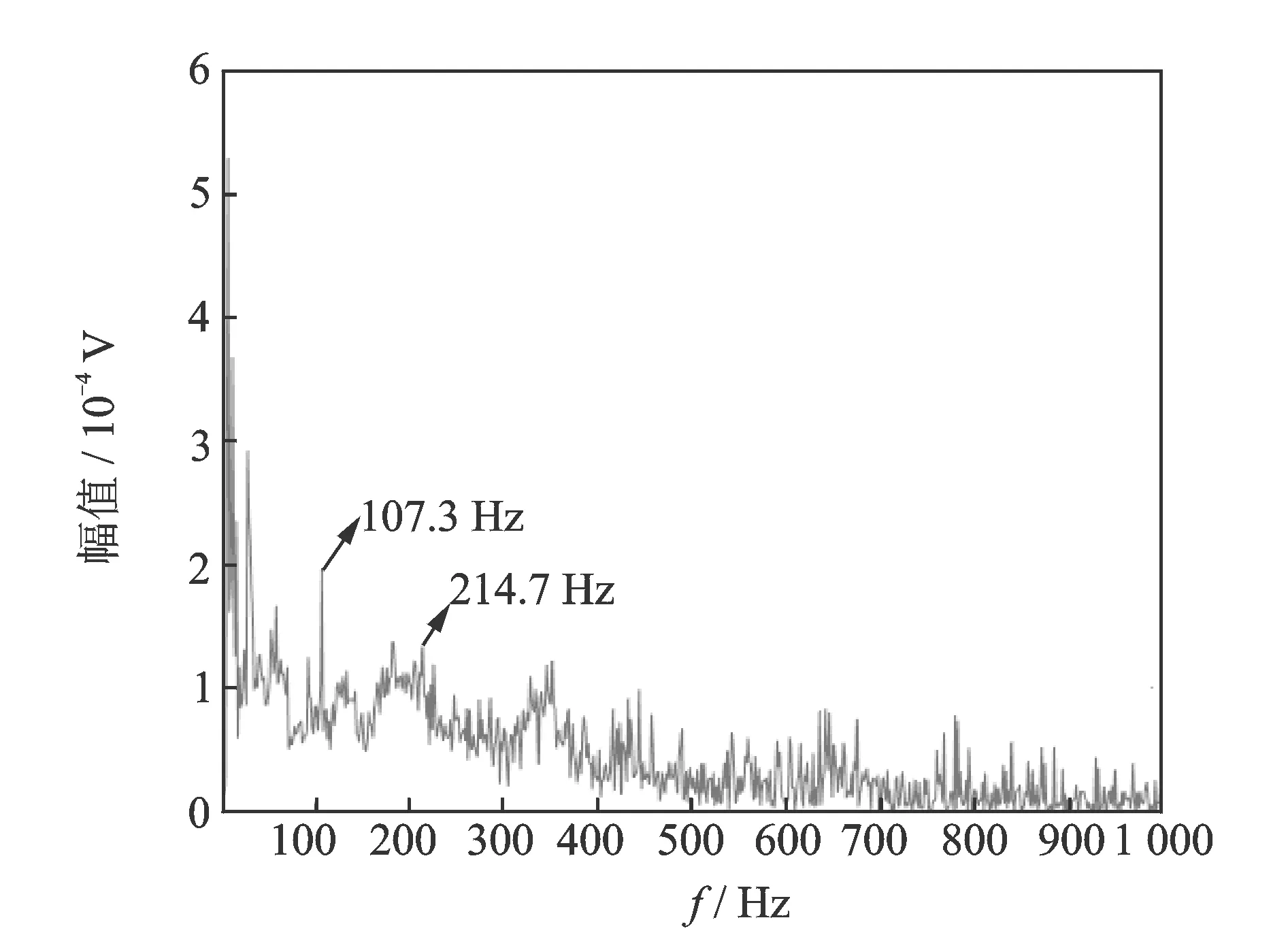

5 结 论

